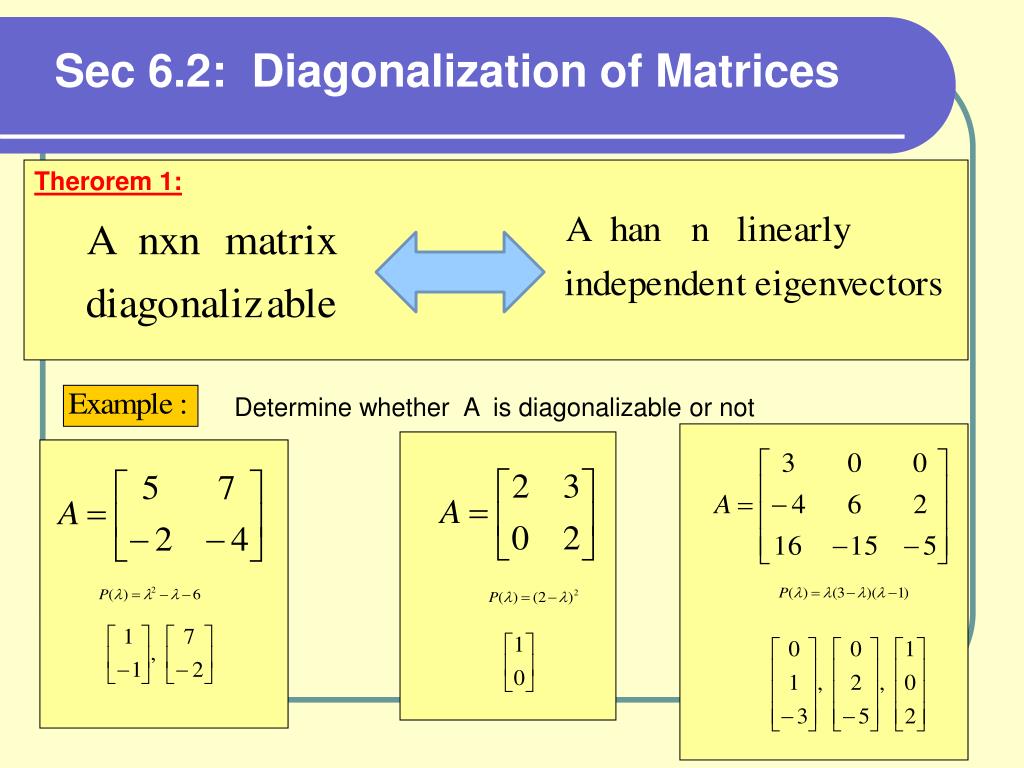
Orthogonal Matrix Implies Diagonalizable . Moreover, the matrix p with. A square matrix $a$ is orthogonally diagonalizable if its eigenvectors are orthogonal *which is the case for any symmetrical matrix). We say a matrix ais diagonalizable if it is similar to a diagonal matrix. This means that there exists an invertible matrix s such that b = s −1 as is. I want to prove that all orthogonal matrices are diagonalizable over $c$. Thus, an orthogonally diagonalizable matrix is a special kind of diagonalizable matrix: An \(n \times n\) matrix \(a\) is orthogonally diagonalizable if there is an orthogonal matrix \(p\) such that \(p^{\tr}ap\) is a diagonal. Not only can we factor e œ t ht ,. 8.2 orthogonal diagonalization recall (theorem 5.5.3) that an n×n matrix a is diagonalizable if and only if it has n linearly independent eigenvectors. Orthogonal matrix is a square matrix with orthonormal columns. I know that a matrix is orthogonal if $q^tq = qq^t = i$ and. Orthogonally diagonalizable matrices 024297 an \(n \times n\) matrix \(a\) is said to be orthogonally diagonalizable when an.
from www.slideserve.com
An \(n \times n\) matrix \(a\) is orthogonally diagonalizable if there is an orthogonal matrix \(p\) such that \(p^{\tr}ap\) is a diagonal. A square matrix $a$ is orthogonally diagonalizable if its eigenvectors are orthogonal *which is the case for any symmetrical matrix). Thus, an orthogonally diagonalizable matrix is a special kind of diagonalizable matrix: This means that there exists an invertible matrix s such that b = s −1 as is. 8.2 orthogonal diagonalization recall (theorem 5.5.3) that an n×n matrix a is diagonalizable if and only if it has n linearly independent eigenvectors. I want to prove that all orthogonal matrices are diagonalizable over $c$. We say a matrix ais diagonalizable if it is similar to a diagonal matrix. Moreover, the matrix p with. I know that a matrix is orthogonal if $q^tq = qq^t = i$ and. Not only can we factor e œ t ht ,.
PPT Diagonal Matrix PowerPoint Presentation, free download ID5424371
Orthogonal Matrix Implies Diagonalizable Not only can we factor e œ t ht ,. An \(n \times n\) matrix \(a\) is orthogonally diagonalizable if there is an orthogonal matrix \(p\) such that \(p^{\tr}ap\) is a diagonal. This means that there exists an invertible matrix s such that b = s −1 as is. Not only can we factor e œ t ht ,. Thus, an orthogonally diagonalizable matrix is a special kind of diagonalizable matrix: I want to prove that all orthogonal matrices are diagonalizable over $c$. I know that a matrix is orthogonal if $q^tq = qq^t = i$ and. 8.2 orthogonal diagonalization recall (theorem 5.5.3) that an n×n matrix a is diagonalizable if and only if it has n linearly independent eigenvectors. A square matrix $a$ is orthogonally diagonalizable if its eigenvectors are orthogonal *which is the case for any symmetrical matrix). Orthogonal matrix is a square matrix with orthonormal columns. We say a matrix ais diagonalizable if it is similar to a diagonal matrix. Orthogonally diagonalizable matrices 024297 an \(n \times n\) matrix \(a\) is said to be orthogonally diagonalizable when an. Moreover, the matrix p with.
From www.slideserve.com
PPT 8.2 Orthogonal Diagonalization PowerPoint Presentation, free Orthogonal Matrix Implies Diagonalizable A square matrix $a$ is orthogonally diagonalizable if its eigenvectors are orthogonal *which is the case for any symmetrical matrix). An \(n \times n\) matrix \(a\) is orthogonally diagonalizable if there is an orthogonal matrix \(p\) such that \(p^{\tr}ap\) is a diagonal. 8.2 orthogonal diagonalization recall (theorem 5.5.3) that an n×n matrix a is diagonalizable if and only if it. Orthogonal Matrix Implies Diagonalizable.
From www.chegg.com
Find an orthogonal diagonalization for Orthogonal Matrix Implies Diagonalizable I know that a matrix is orthogonal if $q^tq = qq^t = i$ and. Not only can we factor e œ t ht ,. An \(n \times n\) matrix \(a\) is orthogonally diagonalizable if there is an orthogonal matrix \(p\) such that \(p^{\tr}ap\) is a diagonal. Moreover, the matrix p with. I want to prove that all orthogonal matrices are. Orthogonal Matrix Implies Diagonalizable.
From www.chegg.com
Solved Orthogonal Diagonalization Orthogonally diagonalize Orthogonal Matrix Implies Diagonalizable 8.2 orthogonal diagonalization recall (theorem 5.5.3) that an n×n matrix a is diagonalizable if and only if it has n linearly independent eigenvectors. I want to prove that all orthogonal matrices are diagonalizable over $c$. Thus, an orthogonally diagonalizable matrix is a special kind of diagonalizable matrix: This means that there exists an invertible matrix s such that b =. Orthogonal Matrix Implies Diagonalizable.
From www.slideserve.com
PPT Diagonal Matrix PowerPoint Presentation, free download ID5424371 Orthogonal Matrix Implies Diagonalizable Orthogonal matrix is a square matrix with orthonormal columns. A square matrix $a$ is orthogonally diagonalizable if its eigenvectors are orthogonal *which is the case for any symmetrical matrix). Moreover, the matrix p with. I know that a matrix is orthogonal if $q^tq = qq^t = i$ and. Orthogonally diagonalizable matrices 024297 an \(n \times n\) matrix \(a\) is said. Orthogonal Matrix Implies Diagonalizable.
From www.youtube.com
Orthogonal Diagonalization of a Symmetric Matrix YouTube Orthogonal Matrix Implies Diagonalizable 8.2 orthogonal diagonalization recall (theorem 5.5.3) that an n×n matrix a is diagonalizable if and only if it has n linearly independent eigenvectors. A square matrix $a$ is orthogonally diagonalizable if its eigenvectors are orthogonal *which is the case for any symmetrical matrix). An \(n \times n\) matrix \(a\) is orthogonally diagonalizable if there is an orthogonal matrix \(p\) such. Orthogonal Matrix Implies Diagonalizable.
From www.youtube.com
Linear Algebra check if a 2x2 matrix is diagonalizable YouTube Orthogonal Matrix Implies Diagonalizable This means that there exists an invertible matrix s such that b = s −1 as is. We say a matrix ais diagonalizable if it is similar to a diagonal matrix. Orthogonal matrix is a square matrix with orthonormal columns. A square matrix $a$ is orthogonally diagonalizable if its eigenvectors are orthogonal *which is the case for any symmetrical matrix).. Orthogonal Matrix Implies Diagonalizable.
From rebeccamorford.blogspot.com
Symmetric Matrix Orthogonally Diagonalizable Rebecca Morford's Orthogonal Matrix Implies Diagonalizable Thus, an orthogonally diagonalizable matrix is a special kind of diagonalizable matrix: I know that a matrix is orthogonal if $q^tq = qq^t = i$ and. Moreover, the matrix p with. Not only can we factor e œ t ht ,. An \(n \times n\) matrix \(a\) is orthogonally diagonalizable if there is an orthogonal matrix \(p\) such that \(p^{\tr}ap\). Orthogonal Matrix Implies Diagonalizable.
From www.slideserve.com
PPT 8.2 Orthogonal Diagonalization PowerPoint Presentation, free Orthogonal Matrix Implies Diagonalizable Orthogonal matrix is a square matrix with orthonormal columns. I know that a matrix is orthogonal if $q^tq = qq^t = i$ and. 8.2 orthogonal diagonalization recall (theorem 5.5.3) that an n×n matrix a is diagonalizable if and only if it has n linearly independent eigenvectors. Thus, an orthogonally diagonalizable matrix is a special kind of diagonalizable matrix: Not only. Orthogonal Matrix Implies Diagonalizable.
From www.youtube.com
Orthogonal Diagonalization YouTube Orthogonal Matrix Implies Diagonalizable A square matrix $a$ is orthogonally diagonalizable if its eigenvectors are orthogonal *which is the case for any symmetrical matrix). Orthogonally diagonalizable matrices 024297 an \(n \times n\) matrix \(a\) is said to be orthogonally diagonalizable when an. We say a matrix ais diagonalizable if it is similar to a diagonal matrix. I want to prove that all orthogonal matrices. Orthogonal Matrix Implies Diagonalizable.
From www.youtube.com
Representation Theory 14, Diagonalizable Matrix YouTube Orthogonal Matrix Implies Diagonalizable I know that a matrix is orthogonal if $q^tq = qq^t = i$ and. This means that there exists an invertible matrix s such that b = s −1 as is. We say a matrix ais diagonalizable if it is similar to a diagonal matrix. Not only can we factor e œ t ht ,. An \(n \times n\) matrix. Orthogonal Matrix Implies Diagonalizable.
From medium.com
[Linear Algebra] 9. Properties of orthogonal matrices by jun94 jun Orthogonal Matrix Implies Diagonalizable 8.2 orthogonal diagonalization recall (theorem 5.5.3) that an n×n matrix a is diagonalizable if and only if it has n linearly independent eigenvectors. Orthogonally diagonalizable matrices 024297 an \(n \times n\) matrix \(a\) is said to be orthogonally diagonalizable when an. Moreover, the matrix p with. Orthogonal matrix is a square matrix with orthonormal columns. I know that a matrix. Orthogonal Matrix Implies Diagonalizable.
From www.studocu.com
Orthonormal Diagonalization 8 Diagonalization of symmetric matrices Orthogonal Matrix Implies Diagonalizable A square matrix $a$ is orthogonally diagonalizable if its eigenvectors are orthogonal *which is the case for any symmetrical matrix). An \(n \times n\) matrix \(a\) is orthogonally diagonalizable if there is an orthogonal matrix \(p\) such that \(p^{\tr}ap\) is a diagonal. Orthogonal matrix is a square matrix with orthonormal columns. I want to prove that all orthogonal matrices are. Orthogonal Matrix Implies Diagonalizable.
From www.chegg.com
Solved Find an orthogonal matrix and a diagonal matrix D Orthogonal Matrix Implies Diagonalizable I know that a matrix is orthogonal if $q^tq = qq^t = i$ and. 8.2 orthogonal diagonalization recall (theorem 5.5.3) that an n×n matrix a is diagonalizable if and only if it has n linearly independent eigenvectors. An \(n \times n\) matrix \(a\) is orthogonally diagonalizable if there is an orthogonal matrix \(p\) such that \(p^{\tr}ap\) is a diagonal. Orthogonally. Orthogonal Matrix Implies Diagonalizable.
From www.youtube.com
Diagonalize 3x3 matrix YouTube Orthogonal Matrix Implies Diagonalizable A square matrix $a$ is orthogonally diagonalizable if its eigenvectors are orthogonal *which is the case for any symmetrical matrix). Orthogonally diagonalizable matrices 024297 an \(n \times n\) matrix \(a\) is said to be orthogonally diagonalizable when an. We say a matrix ais diagonalizable if it is similar to a diagonal matrix. Moreover, the matrix p with. An \(n \times. Orthogonal Matrix Implies Diagonalizable.
From www.chegg.com
Solved Orthogonally diagonalize matrix A given below; that Orthogonal Matrix Implies Diagonalizable Thus, an orthogonally diagonalizable matrix is a special kind of diagonalizable matrix: Moreover, the matrix p with. I want to prove that all orthogonal matrices are diagonalizable over $c$. Orthogonal matrix is a square matrix with orthonormal columns. Not only can we factor e œ t ht ,. An \(n \times n\) matrix \(a\) is orthogonally diagonalizable if there is. Orthogonal Matrix Implies Diagonalizable.
From www.chegg.com
Solved Orthogonally diagonalize the matrix, giving an Orthogonal Matrix Implies Diagonalizable A square matrix $a$ is orthogonally diagonalizable if its eigenvectors are orthogonal *which is the case for any symmetrical matrix). Not only can we factor e œ t ht ,. I want to prove that all orthogonal matrices are diagonalizable over $c$. We say a matrix ais diagonalizable if it is similar to a diagonal matrix. 8.2 orthogonal diagonalization recall. Orthogonal Matrix Implies Diagonalizable.
From www.slideserve.com
PPT 8.2 Orthogonal Diagonalization PowerPoint Presentation, free Orthogonal Matrix Implies Diagonalizable Thus, an orthogonally diagonalizable matrix is a special kind of diagonalizable matrix: I want to prove that all orthogonal matrices are diagonalizable over $c$. Moreover, the matrix p with. Orthogonally diagonalizable matrices 024297 an \(n \times n\) matrix \(a\) is said to be orthogonally diagonalizable when an. An \(n \times n\) matrix \(a\) is orthogonally diagonalizable if there is an. Orthogonal Matrix Implies Diagonalizable.
From www.youtube.com
5 Orthogonal diagonalization of symmetric matrices YouTube Orthogonal Matrix Implies Diagonalizable Moreover, the matrix p with. 8.2 orthogonal diagonalization recall (theorem 5.5.3) that an n×n matrix a is diagonalizable if and only if it has n linearly independent eigenvectors. Orthogonal matrix is a square matrix with orthonormal columns. This means that there exists an invertible matrix s such that b = s −1 as is. Orthogonally diagonalizable matrices 024297 an \(n. Orthogonal Matrix Implies Diagonalizable.
From rebeccamorford.blogspot.com
Symmetric Matrix Orthogonally Diagonalizable Rebecca Morford's Orthogonal Matrix Implies Diagonalizable Moreover, the matrix p with. Orthogonal matrix is a square matrix with orthonormal columns. We say a matrix ais diagonalizable if it is similar to a diagonal matrix. A square matrix $a$ is orthogonally diagonalizable if its eigenvectors are orthogonal *which is the case for any symmetrical matrix). Thus, an orthogonally diagonalizable matrix is a special kind of diagonalizable matrix:. Orthogonal Matrix Implies Diagonalizable.
From www.youtube.com
Week 10 Symmetric matrices and orthogonal diagonalization YouTube Orthogonal Matrix Implies Diagonalizable I know that a matrix is orthogonal if $q^tq = qq^t = i$ and. An \(n \times n\) matrix \(a\) is orthogonally diagonalizable if there is an orthogonal matrix \(p\) such that \(p^{\tr}ap\) is a diagonal. We say a matrix ais diagonalizable if it is similar to a diagonal matrix. I want to prove that all orthogonal matrices are diagonalizable. Orthogonal Matrix Implies Diagonalizable.
From www.youtube.com
Orthogonally Diagonalize a Matrix YouTube Orthogonal Matrix Implies Diagonalizable 8.2 orthogonal diagonalization recall (theorem 5.5.3) that an n×n matrix a is diagonalizable if and only if it has n linearly independent eigenvectors. This means that there exists an invertible matrix s such that b = s −1 as is. I know that a matrix is orthogonal if $q^tq = qq^t = i$ and. An \(n \times n\) matrix \(a\). Orthogonal Matrix Implies Diagonalizable.
From www.chegg.com
Solved Orthogonally diagonalize the matrix below, giving an Orthogonal Matrix Implies Diagonalizable Moreover, the matrix p with. 8.2 orthogonal diagonalization recall (theorem 5.5.3) that an n×n matrix a is diagonalizable if and only if it has n linearly independent eigenvectors. I want to prove that all orthogonal matrices are diagonalizable over $c$. This means that there exists an invertible matrix s such that b = s −1 as is. A square matrix. Orthogonal Matrix Implies Diagonalizable.
From www.youtube.com
Orthogonal Diagonalization of Symmetric Matrix_Easy and Detailed Orthogonal Matrix Implies Diagonalizable Moreover, the matrix p with. A square matrix $a$ is orthogonally diagonalizable if its eigenvectors are orthogonal *which is the case for any symmetrical matrix). We say a matrix ais diagonalizable if it is similar to a diagonal matrix. I know that a matrix is orthogonal if $q^tq = qq^t = i$ and. Orthogonal matrix is a square matrix with. Orthogonal Matrix Implies Diagonalizable.
From www.slideserve.com
PPT Diagonal Matrix PowerPoint Presentation, free download ID5424371 Orthogonal Matrix Implies Diagonalizable Moreover, the matrix p with. I want to prove that all orthogonal matrices are diagonalizable over $c$. We say a matrix ais diagonalizable if it is similar to a diagonal matrix. Thus, an orthogonally diagonalizable matrix is a special kind of diagonalizable matrix: Not only can we factor e œ t ht ,. 8.2 orthogonal diagonalization recall (theorem 5.5.3) that. Orthogonal Matrix Implies Diagonalizable.
From www.studypool.com
SOLUTION Orthogonal Diagonalization of Symmetric Matrices & Exercises Orthogonal Matrix Implies Diagonalizable A square matrix $a$ is orthogonally diagonalizable if its eigenvectors are orthogonal *which is the case for any symmetrical matrix). Thus, an orthogonally diagonalizable matrix is a special kind of diagonalizable matrix: We say a matrix ais diagonalizable if it is similar to a diagonal matrix. I want to prove that all orthogonal matrices are diagonalizable over $c$. This means. Orthogonal Matrix Implies Diagonalizable.
From www.numerade.com
SOLVED 5. Find an orthogonal matrix and & diagonal matrix D to Orthogonal Matrix Implies Diagonalizable Moreover, the matrix p with. We say a matrix ais diagonalizable if it is similar to a diagonal matrix. An \(n \times n\) matrix \(a\) is orthogonally diagonalizable if there is an orthogonal matrix \(p\) such that \(p^{\tr}ap\) is a diagonal. Orthogonal matrix is a square matrix with orthonormal columns. A square matrix $a$ is orthogonally diagonalizable if its eigenvectors. Orthogonal Matrix Implies Diagonalizable.
From www.numerade.com
SOLVED Orthogonally diagonalize the matrix, giving an orthogonal Orthogonal Matrix Implies Diagonalizable We say a matrix ais diagonalizable if it is similar to a diagonal matrix. This means that there exists an invertible matrix s such that b = s −1 as is. Moreover, the matrix p with. Not only can we factor e œ t ht ,. Thus, an orthogonally diagonalizable matrix is a special kind of diagonalizable matrix: Orthogonal matrix. Orthogonal Matrix Implies Diagonalizable.
From rebeccamorford.blogspot.com
Symmetric Matrix Orthogonally Diagonalizable Rebecca Morford's Orthogonal Matrix Implies Diagonalizable Orthogonally diagonalizable matrices 024297 an \(n \times n\) matrix \(a\) is said to be orthogonally diagonalizable when an. I know that a matrix is orthogonal if $q^tq = qq^t = i$ and. 8.2 orthogonal diagonalization recall (theorem 5.5.3) that an n×n matrix a is diagonalizable if and only if it has n linearly independent eigenvectors. Not only can we factor. Orthogonal Matrix Implies Diagonalizable.
From www.chegg.com
Solved Orthogonally diagonalize the matrix, giving an Orthogonal Matrix Implies Diagonalizable Not only can we factor e œ t ht ,. An \(n \times n\) matrix \(a\) is orthogonally diagonalizable if there is an orthogonal matrix \(p\) such that \(p^{\tr}ap\) is a diagonal. Moreover, the matrix p with. I know that a matrix is orthogonal if $q^tq = qq^t = i$ and. A square matrix $a$ is orthogonally diagonalizable if its. Orthogonal Matrix Implies Diagonalizable.
From www.wikihow.com
How to Diagonalize a Matrix StepbyStep Guide and Example Orthogonal Matrix Implies Diagonalizable We say a matrix ais diagonalizable if it is similar to a diagonal matrix. Moreover, the matrix p with. This means that there exists an invertible matrix s such that b = s −1 as is. Orthogonally diagonalizable matrices 024297 an \(n \times n\) matrix \(a\) is said to be orthogonally diagonalizable when an. 8.2 orthogonal diagonalization recall (theorem 5.5.3). Orthogonal Matrix Implies Diagonalizable.
From www.youtube.com
Matrices Diagonales YouTube Orthogonal Matrix Implies Diagonalizable This means that there exists an invertible matrix s such that b = s −1 as is. Orthogonal matrix is a square matrix with orthonormal columns. We say a matrix ais diagonalizable if it is similar to a diagonal matrix. I want to prove that all orthogonal matrices are diagonalizable over $c$. 8.2 orthogonal diagonalization recall (theorem 5.5.3) that an. Orthogonal Matrix Implies Diagonalizable.
From www.youtube.com
Orthogonally Diagonalizable Matrices YouTube Orthogonal Matrix Implies Diagonalizable This means that there exists an invertible matrix s such that b = s −1 as is. 8.2 orthogonal diagonalization recall (theorem 5.5.3) that an n×n matrix a is diagonalizable if and only if it has n linearly independent eigenvectors. We say a matrix ais diagonalizable if it is similar to a diagonal matrix. A square matrix $a$ is orthogonally. Orthogonal Matrix Implies Diagonalizable.
From slidetodoc.com
Chapter Content n n n Eigenvalues and Eigenvectors Orthogonal Matrix Implies Diagonalizable We say a matrix ais diagonalizable if it is similar to a diagonal matrix. I want to prove that all orthogonal matrices are diagonalizable over $c$. Thus, an orthogonally diagonalizable matrix is a special kind of diagonalizable matrix: A square matrix $a$ is orthogonally diagonalizable if its eigenvectors are orthogonal *which is the case for any symmetrical matrix). 8.2 orthogonal. Orthogonal Matrix Implies Diagonalizable.
From www.chegg.com
Solved Find an orthogonal matrix P and a diagonal matrix D Orthogonal Matrix Implies Diagonalizable Orthogonal matrix is a square matrix with orthonormal columns. I know that a matrix is orthogonal if $q^tq = qq^t = i$ and. Thus, an orthogonally diagonalizable matrix is a special kind of diagonalizable matrix: This means that there exists an invertible matrix s such that b = s −1 as is. A square matrix $a$ is orthogonally diagonalizable if. Orthogonal Matrix Implies Diagonalizable.
From www.youtube.com
Orthogonal and Orthonormal vectors and Matrices, Diagonal Matrix Orthogonal Matrix Implies Diagonalizable Not only can we factor e œ t ht ,. This means that there exists an invertible matrix s such that b = s −1 as is. Orthogonal matrix is a square matrix with orthonormal columns. A square matrix $a$ is orthogonally diagonalizable if its eigenvectors are orthogonal *which is the case for any symmetrical matrix). An \(n \times n\). Orthogonal Matrix Implies Diagonalizable.