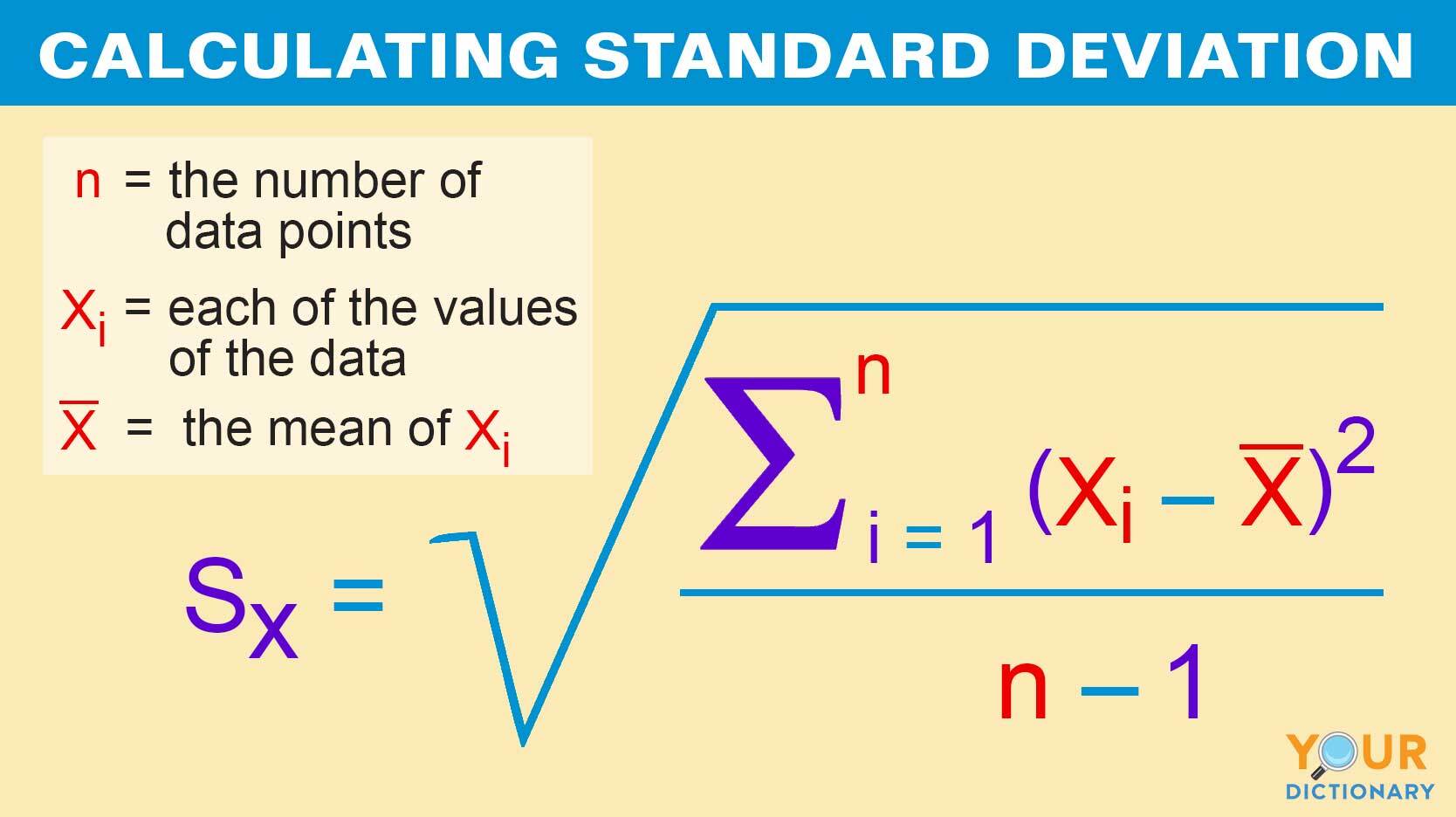
Standard Deviation Probability And Statistics . The standard deviation (sd) is a single number that summarizes the variability in a dataset. The variance is simply the standard deviation squared, so: It tells you, on average, how far each value lies from the mean. The standard deviation is the average amount of variability in your dataset. It represents the typical distance between each data point and the mean. A high standard deviation means. The following examples show how to calculate the standard deviation of a probability distribution in a few other scenarios. The standard deviation of a probability distribution, just like the variance of a probability distribution, is a measurement of the deviation in that probability distribution. Standard deviation = √(.3785 +.0689 +.1059 +.2643 +.1301) = 0.9734.
from examples.yourdictionary.com
Standard deviation = √(.3785 +.0689 +.1059 +.2643 +.1301) = 0.9734. The standard deviation of a probability distribution, just like the variance of a probability distribution, is a measurement of the deviation in that probability distribution. The following examples show how to calculate the standard deviation of a probability distribution in a few other scenarios. It represents the typical distance between each data point and the mean. A high standard deviation means. It tells you, on average, how far each value lies from the mean. The standard deviation (sd) is a single number that summarizes the variability in a dataset. The standard deviation is the average amount of variability in your dataset. The variance is simply the standard deviation squared, so:
Examples of Standard Deviation and How It’s Used
Standard Deviation Probability And Statistics Standard deviation = √(.3785 +.0689 +.1059 +.2643 +.1301) = 0.9734. It tells you, on average, how far each value lies from the mean. A high standard deviation means. The standard deviation (sd) is a single number that summarizes the variability in a dataset. The following examples show how to calculate the standard deviation of a probability distribution in a few other scenarios. Standard deviation = √(.3785 +.0689 +.1059 +.2643 +.1301) = 0.9734. The standard deviation is the average amount of variability in your dataset. The variance is simply the standard deviation squared, so: It represents the typical distance between each data point and the mean. The standard deviation of a probability distribution, just like the variance of a probability distribution, is a measurement of the deviation in that probability distribution.
From www.eajohansson.net
On the Standard Normal Distribution Learn. Adapt. Do. Standard Deviation Probability And Statistics A high standard deviation means. The standard deviation (sd) is a single number that summarizes the variability in a dataset. It tells you, on average, how far each value lies from the mean. It represents the typical distance between each data point and the mean. The following examples show how to calculate the standard deviation of a probability distribution in. Standard Deviation Probability And Statistics.
From simp-link.com
Standard deviation probability calculator Standard Deviation Probability And Statistics It tells you, on average, how far each value lies from the mean. The variance is simply the standard deviation squared, so: A high standard deviation means. The standard deviation is the average amount of variability in your dataset. The following examples show how to calculate the standard deviation of a probability distribution in a few other scenarios. Standard deviation. Standard Deviation Probability And Statistics.
From www.youtube.com
Computing the Mean, Variance and Standard Deviation of a Discrete Standard Deviation Probability And Statistics The standard deviation of a probability distribution, just like the variance of a probability distribution, is a measurement of the deviation in that probability distribution. It represents the typical distance between each data point and the mean. A high standard deviation means. Standard deviation = √(.3785 +.0689 +.1059 +.2643 +.1301) = 0.9734. The standard deviation is the average amount of. Standard Deviation Probability And Statistics.
From www.youtube.com
Discrete Probability Distributions Finding Probabilities, Expected Standard Deviation Probability And Statistics Standard deviation = √(.3785 +.0689 +.1059 +.2643 +.1301) = 0.9734. The variance is simply the standard deviation squared, so: The standard deviation (sd) is a single number that summarizes the variability in a dataset. It represents the typical distance between each data point and the mean. It tells you, on average, how far each value lies from the mean. The. Standard Deviation Probability And Statistics.
From hubpages.com
How to Use Standard Deviation Formula For Equations (Statistics Help Standard Deviation Probability And Statistics The variance is simply the standard deviation squared, so: It represents the typical distance between each data point and the mean. A high standard deviation means. The standard deviation of a probability distribution, just like the variance of a probability distribution, is a measurement of the deviation in that probability distribution. The standard deviation is the average amount of variability. Standard Deviation Probability And Statistics.
From exyrzfyua.blob.core.windows.net
Probability Calculator Using Standard Deviation And Mean at Breanna Standard Deviation Probability And Statistics Standard deviation = √(.3785 +.0689 +.1059 +.2643 +.1301) = 0.9734. The standard deviation (sd) is a single number that summarizes the variability in a dataset. The following examples show how to calculate the standard deviation of a probability distribution in a few other scenarios. The standard deviation is the average amount of variability in your dataset. It tells you, on. Standard Deviation Probability And Statistics.
From www.slideserve.com
PPT Probability Distribution PowerPoint Presentation, free download Standard Deviation Probability And Statistics A high standard deviation means. The variance is simply the standard deviation squared, so: The standard deviation (sd) is a single number that summarizes the variability in a dataset. The following examples show how to calculate the standard deviation of a probability distribution in a few other scenarios. Standard deviation = √(.3785 +.0689 +.1059 +.2643 +.1301) = 0.9734. The standard. Standard Deviation Probability And Statistics.
From www.youtube.com
How To Calculate, Formula For, Variance And Standard Deviation For Standard Deviation Probability And Statistics The variance is simply the standard deviation squared, so: The following examples show how to calculate the standard deviation of a probability distribution in a few other scenarios. The standard deviation (sd) is a single number that summarizes the variability in a dataset. It represents the typical distance between each data point and the mean. The standard deviation is the. Standard Deviation Probability And Statistics.
From www.scribbr.com
The Standard Normal Distribution Examples, Explanations, Uses Standard Deviation Probability And Statistics It tells you, on average, how far each value lies from the mean. The standard deviation of a probability distribution, just like the variance of a probability distribution, is a measurement of the deviation in that probability distribution. The standard deviation (sd) is a single number that summarizes the variability in a dataset. It represents the typical distance between each. Standard Deviation Probability And Statistics.
From quantitative-probabilitydistribution.blogspot.com
Probability Distribution Mean And Standard Deviation Research Topics Standard Deviation Probability And Statistics It tells you, on average, how far each value lies from the mean. The following examples show how to calculate the standard deviation of a probability distribution in a few other scenarios. Standard deviation = √(.3785 +.0689 +.1059 +.2643 +.1301) = 0.9734. The variance is simply the standard deviation squared, so: The standard deviation of a probability distribution, just like. Standard Deviation Probability And Statistics.
From www.wikihow.com
How to Calculate Standard Deviation 12 Steps (with Pictures) Standard Deviation Probability And Statistics Standard deviation = √(.3785 +.0689 +.1059 +.2643 +.1301) = 0.9734. The standard deviation (sd) is a single number that summarizes the variability in a dataset. The variance is simply the standard deviation squared, so: A high standard deviation means. The following examples show how to calculate the standard deviation of a probability distribution in a few other scenarios. The standard. Standard Deviation Probability And Statistics.
From www.youtube.com
Standard Deviation Formula, Statistics, Variance, Sample and Population Standard Deviation Probability And Statistics It represents the typical distance between each data point and the mean. It tells you, on average, how far each value lies from the mean. Standard deviation = √(.3785 +.0689 +.1059 +.2643 +.1301) = 0.9734. The standard deviation (sd) is a single number that summarizes the variability in a dataset. A high standard deviation means. The standard deviation is the. Standard Deviation Probability And Statistics.
From teachoo.com
Example 9 Find variance and standard deviation Class 11 Standard Deviation Probability And Statistics A high standard deviation means. The standard deviation of a probability distribution, just like the variance of a probability distribution, is a measurement of the deviation in that probability distribution. The standard deviation (sd) is a single number that summarizes the variability in a dataset. Standard deviation = √(.3785 +.0689 +.1059 +.2643 +.1301) = 0.9734. The variance is simply the. Standard Deviation Probability And Statistics.
From www.scribbr.com
Normal Distribution Examples, Formulas, & Uses Standard Deviation Probability And Statistics The standard deviation (sd) is a single number that summarizes the variability in a dataset. The following examples show how to calculate the standard deviation of a probability distribution in a few other scenarios. Standard deviation = √(.3785 +.0689 +.1059 +.2643 +.1301) = 0.9734. A high standard deviation means. It tells you, on average, how far each value lies from. Standard Deviation Probability And Statistics.
From curvebreakerstestprep.com
Standard Deviation Variation from the Mean Curvebreakers Standard Deviation Probability And Statistics A high standard deviation means. The standard deviation (sd) is a single number that summarizes the variability in a dataset. Standard deviation = √(.3785 +.0689 +.1059 +.2643 +.1301) = 0.9734. The following examples show how to calculate the standard deviation of a probability distribution in a few other scenarios. The standard deviation of a probability distribution, just like the variance. Standard Deviation Probability And Statistics.
From www.youtube.com
MEAN, VARIANCE AND STANDARD DEVIATION OF PROBABILITY DISTRIBUTION USING Standard Deviation Probability And Statistics Standard deviation = √(.3785 +.0689 +.1059 +.2643 +.1301) = 0.9734. The variance is simply the standard deviation squared, so: The following examples show how to calculate the standard deviation of a probability distribution in a few other scenarios. The standard deviation of a probability distribution, just like the variance of a probability distribution, is a measurement of the deviation in. Standard Deviation Probability And Statistics.
From examples.yourdictionary.com
Examples of Standard Deviation and How It’s Used YourDictionary Standard Deviation Probability And Statistics The following examples show how to calculate the standard deviation of a probability distribution in a few other scenarios. It represents the typical distance between each data point and the mean. The standard deviation is the average amount of variability in your dataset. The variance is simply the standard deviation squared, so: Standard deviation = √(.3785 +.0689 +.1059 +.2643 +.1301). Standard Deviation Probability And Statistics.
From www.wallstreetmojo.com
Standard Normal Distribution Formula What Is It, Examples Standard Deviation Probability And Statistics The variance is simply the standard deviation squared, so: Standard deviation = √(.3785 +.0689 +.1059 +.2643 +.1301) = 0.9734. A high standard deviation means. It represents the typical distance between each data point and the mean. It tells you, on average, how far each value lies from the mean. The standard deviation (sd) is a single number that summarizes the. Standard Deviation Probability And Statistics.
From www.thoughtco.com
How to Calculate a Sample Standard Deviation Standard Deviation Probability And Statistics It tells you, on average, how far each value lies from the mean. The variance is simply the standard deviation squared, so: A high standard deviation means. It represents the typical distance between each data point and the mean. The standard deviation of a probability distribution, just like the variance of a probability distribution, is a measurement of the deviation. Standard Deviation Probability And Statistics.
From www.scribbr.com
Normal Distribution Examples, Formulas, & Uses Standard Deviation Probability And Statistics Standard deviation = √(.3785 +.0689 +.1059 +.2643 +.1301) = 0.9734. The standard deviation is the average amount of variability in your dataset. The variance is simply the standard deviation squared, so: The standard deviation of a probability distribution, just like the variance of a probability distribution, is a measurement of the deviation in that probability distribution. The following examples show. Standard Deviation Probability And Statistics.
From statcalculators.com
Z score Table Standard Normal Distribution Standard Deviation Probability And Statistics The following examples show how to calculate the standard deviation of a probability distribution in a few other scenarios. Standard deviation = √(.3785 +.0689 +.1059 +.2643 +.1301) = 0.9734. It tells you, on average, how far each value lies from the mean. The standard deviation of a probability distribution, just like the variance of a probability distribution, is a measurement. Standard Deviation Probability And Statistics.
From www.teachoo.com
Example 10 Calculate mean, variance, standard deviation Standard Deviation Probability And Statistics It tells you, on average, how far each value lies from the mean. The standard deviation is the average amount of variability in your dataset. The standard deviation of a probability distribution, just like the variance of a probability distribution, is a measurement of the deviation in that probability distribution. A high standard deviation means. The variance is simply the. Standard Deviation Probability And Statistics.
From examples.yourdictionary.com
Examples of Standard Deviation and How It’s Used Standard Deviation Probability And Statistics The following examples show how to calculate the standard deviation of a probability distribution in a few other scenarios. It represents the typical distance between each data point and the mean. The standard deviation of a probability distribution, just like the variance of a probability distribution, is a measurement of the deviation in that probability distribution. The standard deviation (sd). Standard Deviation Probability And Statistics.
From www.youtube.com
Lecture 2 Statistics Variance, Standard Deviation Probability Standard Deviation Probability And Statistics The standard deviation of a probability distribution, just like the variance of a probability distribution, is a measurement of the deviation in that probability distribution. Standard deviation = √(.3785 +.0689 +.1059 +.2643 +.1301) = 0.9734. The following examples show how to calculate the standard deviation of a probability distribution in a few other scenarios. The variance is simply the standard. Standard Deviation Probability And Statistics.
From mavink.com
Standard Deviation Chart Standard Deviation Probability And Statistics The following examples show how to calculate the standard deviation of a probability distribution in a few other scenarios. The variance is simply the standard deviation squared, so: The standard deviation (sd) is a single number that summarizes the variability in a dataset. It tells you, on average, how far each value lies from the mean. The standard deviation of. Standard Deviation Probability And Statistics.
From www.teachoo.com
Example 10 Calculate mean, variance, standard deviation Examples Standard Deviation Probability And Statistics The standard deviation is the average amount of variability in your dataset. The standard deviation of a probability distribution, just like the variance of a probability distribution, is a measurement of the deviation in that probability distribution. The variance is simply the standard deviation squared, so: A high standard deviation means. It represents the typical distance between each data point. Standard Deviation Probability And Statistics.
From www.statology.org
How to Find Probability Given a Mean and Standard Deviation Standard Deviation Probability And Statistics It tells you, on average, how far each value lies from the mean. The variance is simply the standard deviation squared, so: Standard deviation = √(.3785 +.0689 +.1059 +.2643 +.1301) = 0.9734. The standard deviation (sd) is a single number that summarizes the variability in a dataset. It represents the typical distance between each data point and the mean. The. Standard Deviation Probability And Statistics.
From www.researchgate.net
Probability and Standard Deviation by Year Download Table Standard Deviation Probability And Statistics The standard deviation is the average amount of variability in your dataset. The variance is simply the standard deviation squared, so: The standard deviation (sd) is a single number that summarizes the variability in a dataset. A high standard deviation means. It represents the typical distance between each data point and the mean. The standard deviation of a probability distribution,. Standard Deviation Probability And Statistics.
From www.youtube.com
How To Calculate The Standard Deviation YouTube Standard Deviation Probability And Statistics It tells you, on average, how far each value lies from the mean. The standard deviation is the average amount of variability in your dataset. The variance is simply the standard deviation squared, so: It represents the typical distance between each data point and the mean. Standard deviation = √(.3785 +.0689 +.1059 +.2643 +.1301) = 0.9734. The standard deviation of. Standard Deviation Probability And Statistics.
From curvebreakerstestprep.com
Standard Deviation Variation from the Mean Curvebreakers Standard Deviation Probability And Statistics The standard deviation is the average amount of variability in your dataset. The standard deviation (sd) is a single number that summarizes the variability in a dataset. The standard deviation of a probability distribution, just like the variance of a probability distribution, is a measurement of the deviation in that probability distribution. It tells you, on average, how far each. Standard Deviation Probability And Statistics.
From www.vecteezy.com
Gauss distribution. Standard normal distribution. Gaussian bell graph Standard Deviation Probability And Statistics It tells you, on average, how far each value lies from the mean. Standard deviation = √(.3785 +.0689 +.1059 +.2643 +.1301) = 0.9734. A high standard deviation means. The standard deviation is the average amount of variability in your dataset. It represents the typical distance between each data point and the mean. The variance is simply the standard deviation squared,. Standard Deviation Probability And Statistics.
From www.slideserve.com
PPT Statistics Probability Distributions PowerPoint Presentation Standard Deviation Probability And Statistics It tells you, on average, how far each value lies from the mean. The variance is simply the standard deviation squared, so: The standard deviation is the average amount of variability in your dataset. The standard deviation (sd) is a single number that summarizes the variability in a dataset. The following examples show how to calculate the standard deviation of. Standard Deviation Probability And Statistics.
From www.kristakingmath.com
How to find Mean, variance, and standard deviation — Krista King Math Standard Deviation Probability And Statistics The standard deviation is the average amount of variability in your dataset. The following examples show how to calculate the standard deviation of a probability distribution in a few other scenarios. Standard deviation = √(.3785 +.0689 +.1059 +.2643 +.1301) = 0.9734. The standard deviation (sd) is a single number that summarizes the variability in a dataset. A high standard deviation. Standard Deviation Probability And Statistics.
From mrs-mathpedia.com
The Variance and Standard Deviation Mrs.Mathpedia Standard Deviation Probability And Statistics A high standard deviation means. The following examples show how to calculate the standard deviation of a probability distribution in a few other scenarios. It represents the typical distance between each data point and the mean. The standard deviation is the average amount of variability in your dataset. Standard deviation = √(.3785 +.0689 +.1059 +.2643 +.1301) = 0.9734. The standard. Standard Deviation Probability And Statistics.
From www.teachoo.com
Example 12 Calculate mean, variance, standard deviation Standard Deviation Probability And Statistics The standard deviation is the average amount of variability in your dataset. The following examples show how to calculate the standard deviation of a probability distribution in a few other scenarios. The standard deviation (sd) is a single number that summarizes the variability in a dataset. Standard deviation = √(.3785 +.0689 +.1059 +.2643 +.1301) = 0.9734. The variance is simply. Standard Deviation Probability And Statistics.