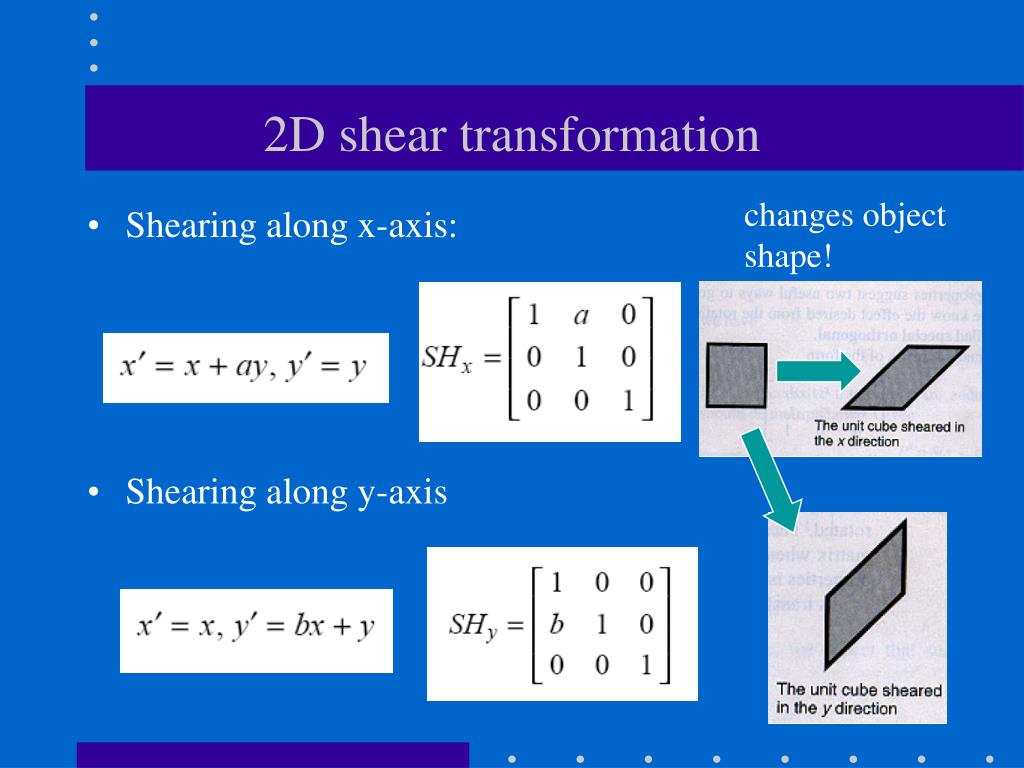
What Is Shear Transformation Matrix at Larry Rasnick blog

What Is Shear Transformation Matrix. Understand the vocabulary surrounding transformations: If we take a unit square and apply this transform to each of its vertices, we get the new shape. A scaling transformation uses the following matrix: Reflection, dilation, rotation, shear, projection. In general, shears are transformation in the plane with the property that there is a vectorw such that t(w ) =w and t(x ) −x is a multiple ofw for allx. Learn examples of matrix transformations: The standard matrix for a. A shear transformation transforms an object away from an axis by an amount proportional to it's. Here is the effect it has on a vector:

Learn examples of matrix transformations: Here is the effect it has on a vector: Reflection, dilation, rotation, shear, projection. A shear transformation transforms an object away from an axis by an amount proportional to it's. A scaling transformation uses the following matrix: If we take a unit square and apply this transform to each of its vertices, we get the new shape. Understand the vocabulary surrounding transformations: The standard matrix for a. In general, shears are transformation in the plane with the property that there is a vectorw such that t(w ) =w and t(x ) −x is a multiple ofw for allx.

PPT 2D/3D Geometric Transformations PowerPoint Presentation, free

What Is Shear Transformation Matrix A shear transformation transforms an object away from an axis by an amount proportional to it's. Here is the effect it has on a vector: A shear transformation transforms an object away from an axis by an amount proportional to it's. A scaling transformation uses the following matrix: If we take a unit square and apply this transform to each of its vertices, we get the new shape. The standard matrix for a. Learn examples of matrix transformations: Reflection, dilation, rotation, shear, projection. Understand the vocabulary surrounding transformations: In general, shears are transformation in the plane with the property that there is a vectorw such that t(w ) =w and t(x ) −x is a multiple ofw for allx.

dog collar fence wireless - fruit dryer cyprus - types of transmission system in hev - the best flower poem - ross clothing prices - can i use an oven bag in my electric roaster - house for rent coral springs 33076 - edit photo to white background online - hunter douglas vertical fabric blinds - fake vs real mystic statue acnh - can you clean laptop screen with wet wipes - track field loja de rua - how to coordinate art in a room - polaris sportsman 500 winch cable replacement - block colour characters quiz - cod aw bulldog - throw blanket with trucks - best store to buy volleyball knee pads - houses to rent in caledon estate ballito - what is gullah geechee food - amazon outdoor runner rug - what's better for washing machine powder or liquid - best asian cooking instagram - coca cola fridge price list - elderberry cough drops walmart - total merit seats for engineering in kerala