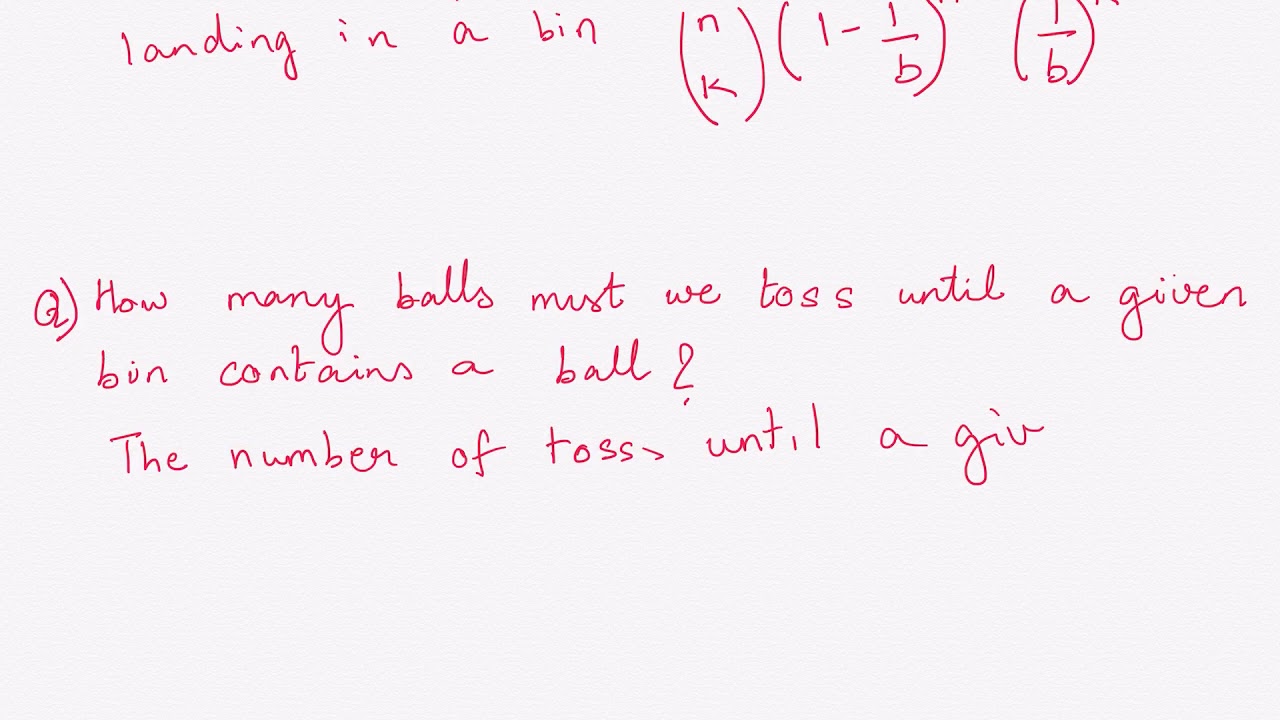Expected Number Of Bins With One Ball . Expected number of balls in a particular bin ? Let $n_i$ be the number of balls in the $i$th bin,. Expected number of balls in a bin, expected number of empty bins, and expected number of bins with r balls. I am trying to compute the expected number of bins with exactly one ball directly. Then, by the linearity of the expectation: To calculate the expected number of bins with one ball, let \(y_i\) be the indicator random variable that bin \(i\) contains exactly one ball. Let z denote the number of bins with at least 1 ball. We also examined the poisson. E[z ∣ x = m] = e[y1 + y2 + ⋯ + ym ∣. • let denote the indicator random variable that ball lands in.
from www.youtube.com
E[z ∣ x = m] = e[y1 + y2 + ⋯ + ym ∣. • let denote the indicator random variable that ball lands in. We also examined the poisson. Expected number of balls in a particular bin ? Let z denote the number of bins with at least 1 ball. Then, by the linearity of the expectation: Let $n_i$ be the number of balls in the $i$th bin,. To calculate the expected number of bins with one ball, let \(y_i\) be the indicator random variable that bin \(i\) contains exactly one ball. Expected number of balls in a bin, expected number of empty bins, and expected number of bins with r balls. I am trying to compute the expected number of bins with exactly one ball directly.
Probability Balls and Bins and Coupon Collector’s Problem YouTube
Expected Number Of Bins With One Ball To calculate the expected number of bins with one ball, let \(y_i\) be the indicator random variable that bin \(i\) contains exactly one ball. We also examined the poisson. I am trying to compute the expected number of bins with exactly one ball directly. Then, by the linearity of the expectation: Expected number of balls in a bin, expected number of empty bins, and expected number of bins with r balls. Let z denote the number of bins with at least 1 ball. Expected number of balls in a particular bin ? Let $n_i$ be the number of balls in the $i$th bin,. • let denote the indicator random variable that ball lands in. E[z ∣ x = m] = e[y1 + y2 + ⋯ + ym ∣. To calculate the expected number of bins with one ball, let \(y_i\) be the indicator random variable that bin \(i\) contains exactly one ball.
From felixfan.github.io
How to set exact number of bins in Histogram in R Expected Number Of Bins With One Ball Let z denote the number of bins with at least 1 ball. I am trying to compute the expected number of bins with exactly one ball directly. Expected number of balls in a bin, expected number of empty bins, and expected number of bins with r balls. We also examined the poisson. Let $n_i$ be the number of balls in. Expected Number Of Bins With One Ball.
From www.youtube.com
The Number of Balls in The Fullest Bin Part 1 YouTube Expected Number Of Bins With One Ball We also examined the poisson. Let $n_i$ be the number of balls in the $i$th bin,. I am trying to compute the expected number of bins with exactly one ball directly. Expected number of balls in a bin, expected number of empty bins, and expected number of bins with r balls. Expected number of balls in a particular bin ?. Expected Number Of Bins With One Ball.
From www.statology.org
R How to Change Number of Bins in Histogram Expected Number Of Bins With One Ball Let z denote the number of bins with at least 1 ball. Expected number of balls in a bin, expected number of empty bins, and expected number of bins with r balls. Expected number of balls in a particular bin ? To calculate the expected number of bins with one ball, let \(y_i\) be the indicator random variable that bin. Expected Number Of Bins With One Ball.
From www.slideserve.com
PPT Randomized Algorithms CS648 PowerPoint Presentation, free Expected Number Of Bins With One Ball To calculate the expected number of bins with one ball, let \(y_i\) be the indicator random variable that bin \(i\) contains exactly one ball. Expected number of balls in a particular bin ? Let $n_i$ be the number of balls in the $i$th bin,. E[z ∣ x = m] = e[y1 + y2 + ⋯ + ym ∣. I am. Expected Number Of Bins With One Ball.
From www.youtube.com
Expected maximum bin load, for balls in bins with equal number of balls Expected Number Of Bins With One Ball Expected number of balls in a particular bin ? To calculate the expected number of bins with one ball, let \(y_i\) be the indicator random variable that bin \(i\) contains exactly one ball. • let denote the indicator random variable that ball lands in. Expected number of balls in a bin, expected number of empty bins, and expected number of. Expected Number Of Bins With One Ball.
From math.stackexchange.com
probability Balls & Bins has N Numbers with Capacity of 1000 each Expected Number Of Bins With One Ball We also examined the poisson. • let denote the indicator random variable that ball lands in. To calculate the expected number of bins with one ball, let \(y_i\) be the indicator random variable that bin \(i\) contains exactly one ball. Let $n_i$ be the number of balls in the $i$th bin,. Then, by the linearity of the expectation: E[z ∣. Expected Number Of Bins With One Ball.
From www.chegg.com
Solved Balls and bins II. Given n balls of each of n Expected Number Of Bins With One Ball Expected number of balls in a bin, expected number of empty bins, and expected number of bins with r balls. • let denote the indicator random variable that ball lands in. I am trying to compute the expected number of bins with exactly one ball directly. Expected number of balls in a particular bin ? Then, by the linearity of. Expected Number Of Bins With One Ball.
From www.youtube.com
Review the balls and bins experiment YouTube Expected Number Of Bins With One Ball To calculate the expected number of bins with one ball, let \(y_i\) be the indicator random variable that bin \(i\) contains exactly one ball. Then, by the linearity of the expectation: I am trying to compute the expected number of bins with exactly one ball directly. Let z denote the number of bins with at least 1 ball. • let. Expected Number Of Bins With One Ball.
From www.pinterest.com
Math Center Activities, Number Activities, Math Activities Preschool Expected Number Of Bins With One Ball Then, by the linearity of the expectation: Let $n_i$ be the number of balls in the $i$th bin,. Expected number of balls in a bin, expected number of empty bins, and expected number of bins with r balls. I am trying to compute the expected number of bins with exactly one ball directly. To calculate the expected number of bins. Expected Number Of Bins With One Ball.
From calcworkshop.com
Binomial Distribution (Fully Explained w/ 11 Examples!) Expected Number Of Bins With One Ball • let denote the indicator random variable that ball lands in. E[z ∣ x = m] = e[y1 + y2 + ⋯ + ym ∣. We also examined the poisson. Expected number of balls in a particular bin ? Expected number of balls in a bin, expected number of empty bins, and expected number of bins with r balls. Then,. Expected Number Of Bins With One Ball.
From www.researchgate.net
Selecting the dimensions for binning and the number of bins. The two Expected Number Of Bins With One Ball Expected number of balls in a particular bin ? I am trying to compute the expected number of bins with exactly one ball directly. Then, by the linearity of the expectation: E[z ∣ x = m] = e[y1 + y2 + ⋯ + ym ∣. To calculate the expected number of bins with one ball, let \(y_i\) be the indicator. Expected Number Of Bins With One Ball.
From statisticsglobe.com
Set Number of Bins for Histogram (2 Examples) Change in R & ggplot2 Expected Number Of Bins With One Ball Expected number of balls in a bin, expected number of empty bins, and expected number of bins with r balls. Then, by the linearity of the expectation: Let $n_i$ be the number of balls in the $i$th bin,. • let denote the indicator random variable that ball lands in. Let z denote the number of bins with at least 1. Expected Number Of Bins With One Ball.
From www.researchgate.net
Rank1 identification versus number of bins. Download Scientific Diagram Expected Number Of Bins With One Ball To calculate the expected number of bins with one ball, let \(y_i\) be the indicator random variable that bin \(i\) contains exactly one ball. E[z ∣ x = m] = e[y1 + y2 + ⋯ + ym ∣. Expected number of balls in a bin, expected number of empty bins, and expected number of bins with r balls. I am. Expected Number Of Bins With One Ball.
From slideplayer.com
Randomized Algorithms CS ppt download Expected Number Of Bins With One Ball E[z ∣ x = m] = e[y1 + y2 + ⋯ + ym ∣. I am trying to compute the expected number of bins with exactly one ball directly. Let z denote the number of bins with at least 1 ball. Expected number of balls in a bin, expected number of empty bins, and expected number of bins with r. Expected Number Of Bins With One Ball.
From www.youtube.com
MAT202 The Balls in Bins Formula YouTube Expected Number Of Bins With One Ball Let $n_i$ be the number of balls in the $i$th bin,. We also examined the poisson. E[z ∣ x = m] = e[y1 + y2 + ⋯ + ym ∣. Expected number of balls in a bin, expected number of empty bins, and expected number of bins with r balls. Let z denote the number of bins with at least. Expected Number Of Bins With One Ball.
From www.slideserve.com
PPT ENGG2012B Lecture 14 Counting & Probability PowerPoint Expected Number Of Bins With One Ball Expected number of balls in a bin, expected number of empty bins, and expected number of bins with r balls. • let denote the indicator random variable that ball lands in. I am trying to compute the expected number of bins with exactly one ball directly. Expected number of balls in a particular bin ? To calculate the expected number. Expected Number Of Bins With One Ball.
From www.researchgate.net
The relation between the number of bins, h, and the size of each bin Expected Number Of Bins With One Ball To calculate the expected number of bins with one ball, let \(y_i\) be the indicator random variable that bin \(i\) contains exactly one ball. We also examined the poisson. Let z denote the number of bins with at least 1 ball. Expected number of balls in a bin, expected number of empty bins, and expected number of bins with r. Expected Number Of Bins With One Ball.
From math.stackexchange.com
combinatorics Number of combinations of distributing n balls of k Expected Number Of Bins With One Ball Then, by the linearity of the expectation: Expected number of balls in a particular bin ? E[z ∣ x = m] = e[y1 + y2 + ⋯ + ym ∣. Let z denote the number of bins with at least 1 ball. We also examined the poisson. Let $n_i$ be the number of balls in the $i$th bin,. To calculate. Expected Number Of Bins With One Ball.
From www.chegg.com
Balls in Bins Estimation We throw n > 0 balls into m Expected Number Of Bins With One Ball We also examined the poisson. • let denote the indicator random variable that ball lands in. I am trying to compute the expected number of bins with exactly one ball directly. Let z denote the number of bins with at least 1 ball. E[z ∣ x = m] = e[y1 + y2 + ⋯ + ym ∣. Expected number of. Expected Number Of Bins With One Ball.
From www.researchgate.net
Illustrating N balls and n bins. Download Scientific Diagram Expected Number Of Bins With One Ball Expected number of balls in a bin, expected number of empty bins, and expected number of bins with r balls. To calculate the expected number of bins with one ball, let \(y_i\) be the indicator random variable that bin \(i\) contains exactly one ball. Then, by the linearity of the expectation: Expected number of balls in a particular bin ?. Expected Number Of Bins With One Ball.
From www.chegg.com
3 Balls and bins Suppose that there are n balls and n Expected Number Of Bins With One Ball We also examined the poisson. Then, by the linearity of the expectation: E[z ∣ x = m] = e[y1 + y2 + ⋯ + ym ∣. Let z denote the number of bins with at least 1 ball. I am trying to compute the expected number of bins with exactly one ball directly. Expected number of balls in a bin,. Expected Number Of Bins With One Ball.
From www.youtube.com
Probability Balls and Bins and Coupon Collector’s Problem YouTube Expected Number Of Bins With One Ball Let $n_i$ be the number of balls in the $i$th bin,. To calculate the expected number of bins with one ball, let \(y_i\) be the indicator random variable that bin \(i\) contains exactly one ball. Expected number of balls in a bin, expected number of empty bins, and expected number of bins with r balls. Expected number of balls in. Expected Number Of Bins With One Ball.
From www.researchgate.net
The ballsintobins problem where we have k blue bins, mk red bins Expected Number Of Bins With One Ball To calculate the expected number of bins with one ball, let \(y_i\) be the indicator random variable that bin \(i\) contains exactly one ball. • let denote the indicator random variable that ball lands in. Let $n_i$ be the number of balls in the $i$th bin,. I am trying to compute the expected number of bins with exactly one ball. Expected Number Of Bins With One Ball.
From www.geeksforgeeks.org
How to Change Number of Bins in Histogram in R? Expected Number Of Bins With One Ball We also examined the poisson. I am trying to compute the expected number of bins with exactly one ball directly. To calculate the expected number of bins with one ball, let \(y_i\) be the indicator random variable that bin \(i\) contains exactly one ball. Then, by the linearity of the expectation: Expected number of balls in a bin, expected number. Expected Number Of Bins With One Ball.
From spreadcheaters.com
How To Change The Number Of Bins In An Excel Histogram SpreadCheaters Expected Number Of Bins With One Ball E[z ∣ x = m] = e[y1 + y2 + ⋯ + ym ∣. Expected number of balls in a bin, expected number of empty bins, and expected number of bins with r balls. Then, by the linearity of the expectation: To calculate the expected number of bins with one ball, let \(y_i\) be the indicator random variable that bin. Expected Number Of Bins With One Ball.
From www.statology.org
R How to Change Number of Bins in Histogram Expected Number Of Bins With One Ball To calculate the expected number of bins with one ball, let \(y_i\) be the indicator random variable that bin \(i\) contains exactly one ball. Expected number of balls in a bin, expected number of empty bins, and expected number of bins with r balls. We also examined the poisson. Let z denote the number of bins with at least 1. Expected Number Of Bins With One Ball.
From www.geeksforgeeks.org
How to Change Number of Bins in Histogram in R? Expected Number Of Bins With One Ball E[z ∣ x = m] = e[y1 + y2 + ⋯ + ym ∣. Then, by the linearity of the expectation: Let $n_i$ be the number of balls in the $i$th bin,. Expected number of balls in a particular bin ? To calculate the expected number of bins with one ball, let \(y_i\) be the indicator random variable that bin. Expected Number Of Bins With One Ball.
From www.exceldemy.com
What Is Bin Range in Excel Histogram? (Uses & Applications) Expected Number Of Bins With One Ball Expected number of balls in a particular bin ? E[z ∣ x = m] = e[y1 + y2 + ⋯ + ym ∣. Then, by the linearity of the expectation: To calculate the expected number of bins with one ball, let \(y_i\) be the indicator random variable that bin \(i\) contains exactly one ball. Let z denote the number of. Expected Number Of Bins With One Ball.
From www.youtube.com
Lesson 24 Balls, bins, hashing YouTube Expected Number Of Bins With One Ball Let $n_i$ be the number of balls in the $i$th bin,. I am trying to compute the expected number of bins with exactly one ball directly. • let denote the indicator random variable that ball lands in. Expected number of balls in a bin, expected number of empty bins, and expected number of bins with r balls. We also examined. Expected Number Of Bins With One Ball.
From www.youtube.com
Probabilistic Analysis Balls and Bins YouTube Expected Number Of Bins With One Ball • let denote the indicator random variable that ball lands in. Expected number of balls in a bin, expected number of empty bins, and expected number of bins with r balls. We also examined the poisson. To calculate the expected number of bins with one ball, let \(y_i\) be the indicator random variable that bin \(i\) contains exactly one ball.. Expected Number Of Bins With One Ball.
From www.youtube.com
Counting the number of ways to place identical balls in distinct bins Expected Number Of Bins With One Ball Let z denote the number of bins with at least 1 ball. E[z ∣ x = m] = e[y1 + y2 + ⋯ + ym ∣. Let $n_i$ be the number of balls in the $i$th bin,. We also examined the poisson. To calculate the expected number of bins with one ball, let \(y_i\) be the indicator random variable that. Expected Number Of Bins With One Ball.
From www.statology.org
How to Adjust Bin Size in Matplotlib Histograms Expected Number Of Bins With One Ball Let z denote the number of bins with at least 1 ball. • let denote the indicator random variable that ball lands in. I am trying to compute the expected number of bins with exactly one ball directly. Expected number of balls in a bin, expected number of empty bins, and expected number of bins with r balls. Let $n_i$. Expected Number Of Bins With One Ball.
From www.researchgate.net
Average number of bins associated with the optimal solutions to the Expected Number Of Bins With One Ball To calculate the expected number of bins with one ball, let \(y_i\) be the indicator random variable that bin \(i\) contains exactly one ball. • let denote the indicator random variable that ball lands in. Let z denote the number of bins with at least 1 ball. We also examined the poisson. Expected number of balls in a particular bin. Expected Number Of Bins With One Ball.
From www.chegg.com
Solved There are k bins, and kn balls. Only one ball is Expected Number Of Bins With One Ball E[z ∣ x = m] = e[y1 + y2 + ⋯ + ym ∣. Let $n_i$ be the number of balls in the $i$th bin,. Expected number of balls in a particular bin ? To calculate the expected number of bins with one ball, let \(y_i\) be the indicator random variable that bin \(i\) contains exactly one ball. I am. Expected Number Of Bins With One Ball.
From www.slideserve.com
PPT Balls into Bins From Theory to Practice to Theory PowerPoint Expected Number Of Bins With One Ball Let z denote the number of bins with at least 1 ball. Expected number of balls in a bin, expected number of empty bins, and expected number of bins with r balls. To calculate the expected number of bins with one ball, let \(y_i\) be the indicator random variable that bin \(i\) contains exactly one ball. Expected number of balls. Expected Number Of Bins With One Ball.