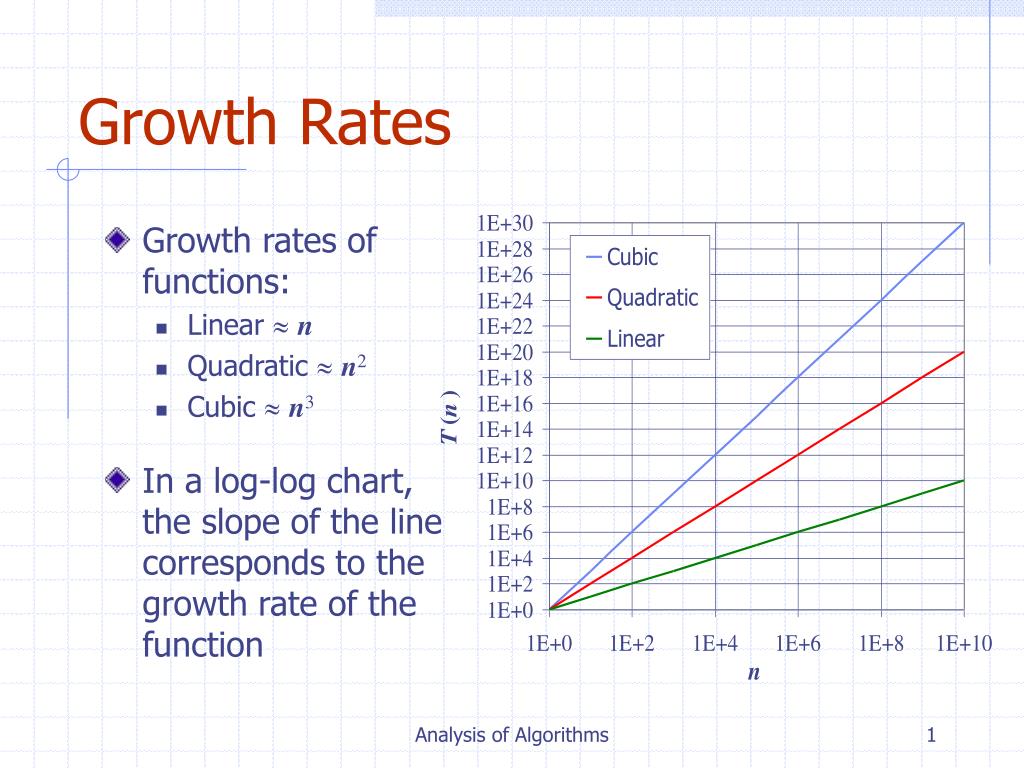
Growth Rates Differential Equation at Krystal Russell blog

Growth Rates Differential Equation. The key model for growth (or decay when c < 0) is dy/dt = c y (t) the next model allows a steady source. A differential equation for exponential growth and decay. How can we assess the accuracy. In the above equation, k is the same carrying capacity or equilibrium value as we discussed. That is, the rate of growth is proportional to the current function value. How can we use differential equations to realistically model the growth of a population? Therefore the differential equation states that the rate at which the population increases is proportional to the population at that point in. The rate is symbolized as dn/dt which simply means “change in n relative to change in t,” and if you recall your basic calculus, we can find the rate of growth by differentiating equation 4. Dx dt = kx, where t and x are variables and k is a constant with k ≠. (differential equation for logistic growth) where r = r0k. This is a key feature of exponential growth. Recall the derivation of a model for human population growth and describe how it leads to a differential equation.

In the above equation, k is the same carrying capacity or equilibrium value as we discussed. Therefore the differential equation states that the rate at which the population increases is proportional to the population at that point in. Recall the derivation of a model for human population growth and describe how it leads to a differential equation. That is, the rate of growth is proportional to the current function value. The key model for growth (or decay when c < 0) is dy/dt = c y (t) the next model allows a steady source. How can we assess the accuracy. A differential equation for exponential growth and decay. Dx dt = kx, where t and x are variables and k is a constant with k ≠. How can we use differential equations to realistically model the growth of a population? This is a key feature of exponential growth.

PPT Growth Rates PowerPoint Presentation, free download ID4208740

Growth Rates Differential Equation Recall the derivation of a model for human population growth and describe how it leads to a differential equation. How can we use differential equations to realistically model the growth of a population? How can we assess the accuracy. In the above equation, k is the same carrying capacity or equilibrium value as we discussed. This is a key feature of exponential growth. That is, the rate of growth is proportional to the current function value. The rate is symbolized as dn/dt which simply means “change in n relative to change in t,” and if you recall your basic calculus, we can find the rate of growth by differentiating equation 4. (differential equation for logistic growth) where r = r0k. A differential equation for exponential growth and decay. Dx dt = kx, where t and x are variables and k is a constant with k ≠. Therefore the differential equation states that the rate at which the population increases is proportional to the population at that point in. Recall the derivation of a model for human population growth and describe how it leads to a differential equation. The key model for growth (or decay when c < 0) is dy/dt = c y (t) the next model allows a steady source.