What Is A Spline In Statistics at Rachel Shortland blog

What Is A Spline In Statistics. We want the function \(f\) in \(y= f(x) + \epsilon\) to: In essence, splines are piecewise polynomials, joined at points called knots. Let’s see how this is done in r. We can also take sample size into. That is, the first derivative is continuous, the second. Splines# cubic splines# define a set of knots \(\xi_1< \xi_2 < \dots<\xi_k\). Lets see how cubic splines, natural cubic splines and smoothing splines compare on the wage data. Each click also creates what’s called a control point , or points that determine the shape of the curve. Click here for further information. What is spline in statistics and how is it related to regression analysis? Splines add curves together to make a continuous and irregular curves. When using this tool, each click created a new area to the line, or a line segment. The terms of the form (u) + have the value u if u is positive, and 0 otherwise. The degree specifies the degree of the polynomials. We call this linear spline regression.

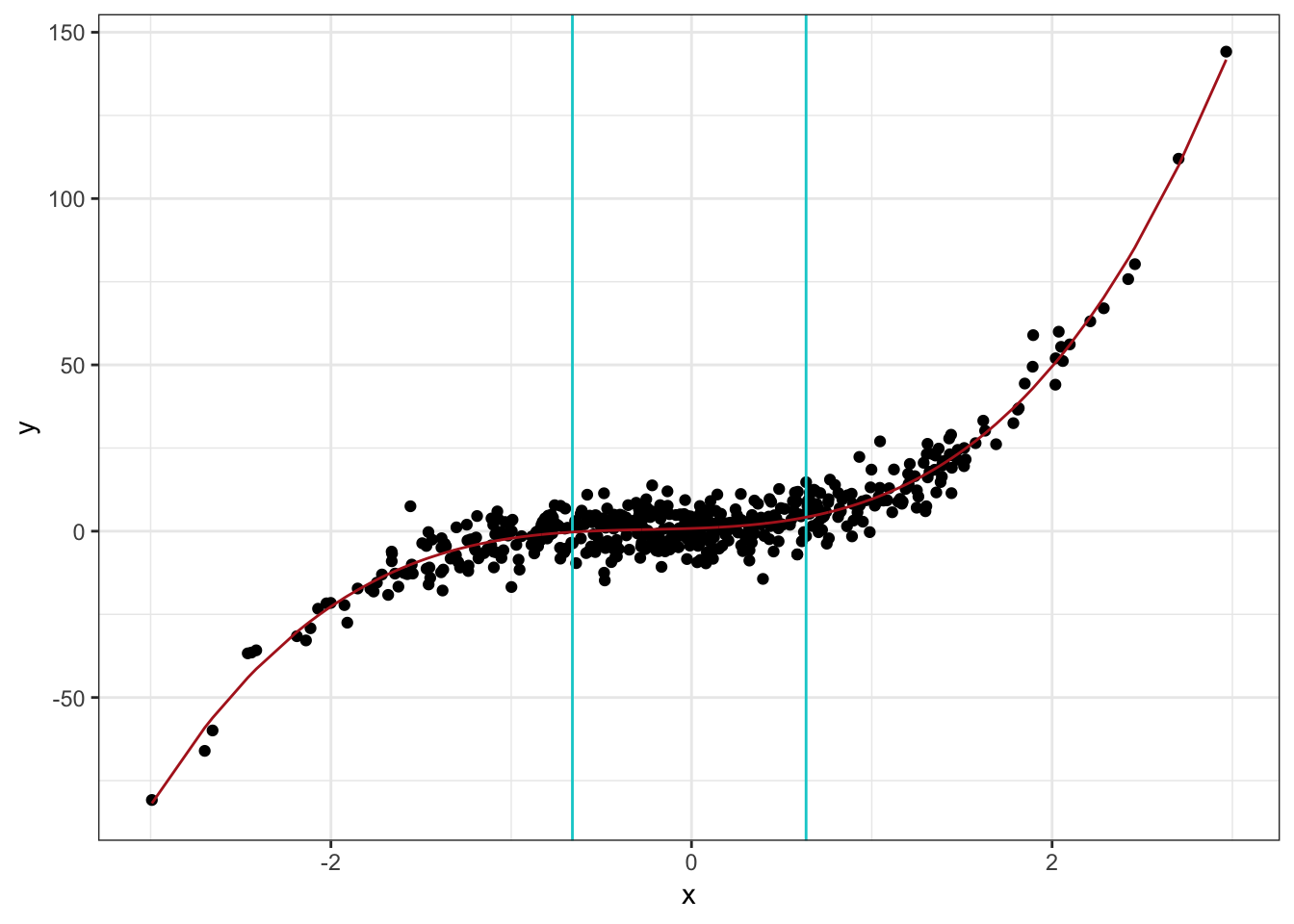
Lets see how cubic splines, natural cubic splines and smoothing splines compare on the wage data. In essence, splines are piecewise polynomials, joined at points called knots. When using this tool, each click created a new area to the line, or a line segment. We want the function \(f\) in \(y= f(x) + \epsilon\) to: What is spline in statistics and how is it related to regression analysis? The terms of the form (u) + have the value u if u is positive, and 0 otherwise. Splines add curves together to make a continuous and irregular curves. We can also take sample size into. Each click also creates what’s called a control point , or points that determine the shape of the curve. That is, the first derivative is continuous, the second.

Splines What Are They? Some Clever Stats Name

What Is A Spline In Statistics Let’s see how this is done in r. That is, the first derivative is continuous, the second. We want the function \(f\) in \(y= f(x) + \epsilon\) to: When using this tool, each click created a new area to the line, or a line segment. We call this linear spline regression. What is spline in statistics and how is it related to regression analysis? Lets see how cubic splines, natural cubic splines and smoothing splines compare on the wage data. Splines add curves together to make a continuous and irregular curves. The degree specifies the degree of the polynomials. The terms of the form (u) + have the value u if u is positive, and 0 otherwise. Click here for further information. Each click also creates what’s called a control point , or points that determine the shape of the curve. Let’s see how this is done in r. We can also take sample size into. Splines# cubic splines# define a set of knots \(\xi_1< \xi_2 < \dots<\xi_k\). In essence, splines are piecewise polynomials, joined at points called knots.