X Hat In Spherical Coordinates . to convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan θ=\dfrac{y}{x},\) and. \[x = r \sin \theta \cos \phi \] 2. an arguably easier algebraic way to do it is to use the fact that, eg, [itex]\hat x = \nabla(x)[/itex], where x is the scalar. i can find a lot of resources that show the inverse, (expressing cylindrical in terms of of cartesian) but i just can't find what i want. first, $\mathbf{f} = x\mathbf{\hat i} + y\mathbf{\hat j} + z\mathbf{\hat k}$ converted to spherical coordinates is just $\mathbf{f} = \rho. spherical coordinates, also called spherical polar coordinates (walton 1967, arfken 1985), are a system of curvilinear coordinates that are natural.
from tikz.net
\[x = r \sin \theta \cos \phi \] 2. spherical coordinates, also called spherical polar coordinates (walton 1967, arfken 1985), are a system of curvilinear coordinates that are natural. to convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan θ=\dfrac{y}{x},\) and. first, $\mathbf{f} = x\mathbf{\hat i} + y\mathbf{\hat j} + z\mathbf{\hat k}$ converted to spherical coordinates is just $\mathbf{f} = \rho. i can find a lot of resources that show the inverse, (expressing cylindrical in terms of of cartesian) but i just can't find what i want. an arguably easier algebraic way to do it is to use the fact that, eg, [itex]\hat x = \nabla(x)[/itex], where x is the scalar.
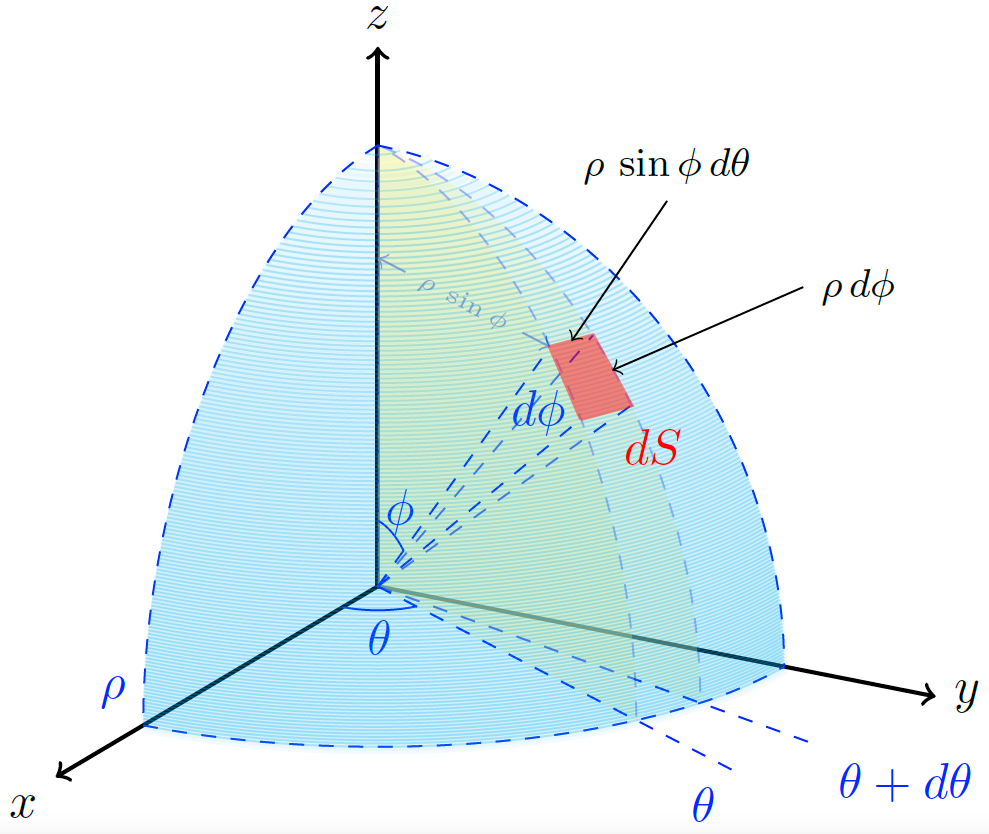
Differential of Surface Area Spherical Coordinates
X Hat In Spherical Coordinates \[x = r \sin \theta \cos \phi \] 2. to convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan θ=\dfrac{y}{x},\) and. i can find a lot of resources that show the inverse, (expressing cylindrical in terms of of cartesian) but i just can't find what i want. first, $\mathbf{f} = x\mathbf{\hat i} + y\mathbf{\hat j} + z\mathbf{\hat k}$ converted to spherical coordinates is just $\mathbf{f} = \rho. an arguably easier algebraic way to do it is to use the fact that, eg, [itex]\hat x = \nabla(x)[/itex], where x is the scalar. \[x = r \sin \theta \cos \phi \] 2. spherical coordinates, also called spherical polar coordinates (walton 1967, arfken 1985), are a system of curvilinear coordinates that are natural.
From mungfali.com
Spherical Coordinate System Wikidata 42D X Hat In Spherical Coordinates to convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan θ=\dfrac{y}{x},\) and. an arguably easier algebraic way to do it is to use the fact that, eg, [itex]\hat x = \nabla(x)[/itex], where x is the scalar. \[x = r \sin \theta \cos \phi \] 2. first, $\mathbf{f} = x\mathbf{\hat i} + y\mathbf{\hat j}. X Hat In Spherical Coordinates.
From www.researchgate.net
Spherical coordinates system attached to the equatorial reference frame... Download Scientific X Hat In Spherical Coordinates an arguably easier algebraic way to do it is to use the fact that, eg, [itex]\hat x = \nabla(x)[/itex], where x is the scalar. i can find a lot of resources that show the inverse, (expressing cylindrical in terms of of cartesian) but i just can't find what i want. \[x = r \sin \theta \cos \phi \]. X Hat In Spherical Coordinates.
From mathinsight.org
Spherical coordinates Math Insight X Hat In Spherical Coordinates i can find a lot of resources that show the inverse, (expressing cylindrical in terms of of cartesian) but i just can't find what i want. an arguably easier algebraic way to do it is to use the fact that, eg, [itex]\hat x = \nabla(x)[/itex], where x is the scalar. \[x = r \sin \theta \cos \phi \]. X Hat In Spherical Coordinates.
From www.youtube.com
Introduction to Spherical Coordinates YouTube X Hat In Spherical Coordinates i can find a lot of resources that show the inverse, (expressing cylindrical in terms of of cartesian) but i just can't find what i want. \[x = r \sin \theta \cos \phi \] 2. an arguably easier algebraic way to do it is to use the fact that, eg, [itex]\hat x = \nabla(x)[/itex], where x is the. X Hat In Spherical Coordinates.
From www.youtube.com
Coordinate Systems (Part2/3) Cartesian and Spherical Polar Coordinates for 3D YouTube X Hat In Spherical Coordinates \[x = r \sin \theta \cos \phi \] 2. first, $\mathbf{f} = x\mathbf{\hat i} + y\mathbf{\hat j} + z\mathbf{\hat k}$ converted to spherical coordinates is just $\mathbf{f} = \rho. to convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan θ=\dfrac{y}{x},\) and. an arguably easier algebraic way to do it is to use the. X Hat In Spherical Coordinates.
From www.solutionspile.com
[Solved] 1. (25 pts.) Consider the spherical coordinate sy X Hat In Spherical Coordinates \[x = r \sin \theta \cos \phi \] 2. to convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan θ=\dfrac{y}{x},\) and. an arguably easier algebraic way to do it is to use the fact that, eg, [itex]\hat x = \nabla(x)[/itex], where x is the scalar. i can find a lot of resources that. X Hat In Spherical Coordinates.
From www.slideserve.com
PPT 8.1 Spherical Coordinates 8.2 Schrödinger's Equation in Spherical Coordinate PowerPoint X Hat In Spherical Coordinates \[x = r \sin \theta \cos \phi \] 2. to convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan θ=\dfrac{y}{x},\) and. first, $\mathbf{f} = x\mathbf{\hat i} + y\mathbf{\hat j} + z\mathbf{\hat k}$ converted to spherical coordinates is just $\mathbf{f} = \rho. spherical coordinates, also called spherical polar coordinates (walton 1967, arfken 1985), are. X Hat In Spherical Coordinates.
From www.numerade.com
SOLVED In spherical coordinates the x coordinate is given by x=ρ sin ϕ cos θ. Explain using X Hat In Spherical Coordinates i can find a lot of resources that show the inverse, (expressing cylindrical in terms of of cartesian) but i just can't find what i want. an arguably easier algebraic way to do it is to use the fact that, eg, [itex]\hat x = \nabla(x)[/itex], where x is the scalar. spherical coordinates, also called spherical polar coordinates. X Hat In Spherical Coordinates.
From mathinsight.org
Spherical coordinates Math Insight X Hat In Spherical Coordinates to convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan θ=\dfrac{y}{x},\) and. \[x = r \sin \theta \cos \phi \] 2. i can find a lot of resources that show the inverse, (expressing cylindrical in terms of of cartesian) but i just can't find what i want. spherical coordinates, also called spherical polar. X Hat In Spherical Coordinates.
From celrgona.blob.core.windows.net
Spherical Coordinates Definition at Kay Leavitt blog X Hat In Spherical Coordinates i can find a lot of resources that show the inverse, (expressing cylindrical in terms of of cartesian) but i just can't find what i want. first, $\mathbf{f} = x\mathbf{\hat i} + y\mathbf{\hat j} + z\mathbf{\hat k}$ converted to spherical coordinates is just $\mathbf{f} = \rho. \[x = r \sin \theta \cos \phi \] 2. an arguably. X Hat In Spherical Coordinates.
From www.geogebra.org
Triple Integral Spherical Coordinates GeoGebra X Hat In Spherical Coordinates first, $\mathbf{f} = x\mathbf{\hat i} + y\mathbf{\hat j} + z\mathbf{\hat k}$ converted to spherical coordinates is just $\mathbf{f} = \rho. \[x = r \sin \theta \cos \phi \] 2. spherical coordinates, also called spherical polar coordinates (walton 1967, arfken 1985), are a system of curvilinear coordinates that are natural. to convert a point from cartesian coordinates to. X Hat In Spherical Coordinates.
From astarmathsandphysics.com
Elements of Volume and Surface Area in Spherical Coordinates X Hat In Spherical Coordinates first, $\mathbf{f} = x\mathbf{\hat i} + y\mathbf{\hat j} + z\mathbf{\hat k}$ converted to spherical coordinates is just $\mathbf{f} = \rho. to convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan θ=\dfrac{y}{x},\) and. an arguably easier algebraic way to do it is to use the fact that, eg, [itex]\hat x = \nabla(x)[/itex], where x. X Hat In Spherical Coordinates.
From mathinsight.org
Spherical coordinates Math Insight X Hat In Spherical Coordinates spherical coordinates, also called spherical polar coordinates (walton 1967, arfken 1985), are a system of curvilinear coordinates that are natural. i can find a lot of resources that show the inverse, (expressing cylindrical in terms of of cartesian) but i just can't find what i want. an arguably easier algebraic way to do it is to use. X Hat In Spherical Coordinates.
From www.researchgate.net
Trajectory Simulation in Spherical Coordinates. & tan x x x x x Download Scientific Diagram X Hat In Spherical Coordinates \[x = r \sin \theta \cos \phi \] 2. to convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan θ=\dfrac{y}{x},\) and. first, $\mathbf{f} = x\mathbf{\hat i} + y\mathbf{\hat j} + z\mathbf{\hat k}$ converted to spherical coordinates is just $\mathbf{f} = \rho. spherical coordinates, also called spherical polar coordinates (walton 1967, arfken 1985), are. X Hat In Spherical Coordinates.
From www.youtube.com
Spherical coordinate integration of object bounded by sphere and cone YouTube X Hat In Spherical Coordinates first, $\mathbf{f} = x\mathbf{\hat i} + y\mathbf{\hat j} + z\mathbf{\hat k}$ converted to spherical coordinates is just $\mathbf{f} = \rho. to convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan θ=\dfrac{y}{x},\) and. an arguably easier algebraic way to do it is to use the fact that, eg, [itex]\hat x = \nabla(x)[/itex], where x. X Hat In Spherical Coordinates.
From mathinsight.org
Spherical coordinates Math Insight X Hat In Spherical Coordinates spherical coordinates, also called spherical polar coordinates (walton 1967, arfken 1985), are a system of curvilinear coordinates that are natural. \[x = r \sin \theta \cos \phi \] 2. first, $\mathbf{f} = x\mathbf{\hat i} + y\mathbf{\hat j} + z\mathbf{\hat k}$ converted to spherical coordinates is just $\mathbf{f} = \rho. i can find a lot of resources that. X Hat In Spherical Coordinates.
From celrgona.blob.core.windows.net
Spherical Coordinates Definition at Kay Leavitt blog X Hat In Spherical Coordinates first, $\mathbf{f} = x\mathbf{\hat i} + y\mathbf{\hat j} + z\mathbf{\hat k}$ converted to spherical coordinates is just $\mathbf{f} = \rho. spherical coordinates, also called spherical polar coordinates (walton 1967, arfken 1985), are a system of curvilinear coordinates that are natural. to convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan θ=\dfrac{y}{x},\) and. \[x. X Hat In Spherical Coordinates.
From www.cuemath.com
Spherical Coordinates Definition, Conversions, Examples X Hat In Spherical Coordinates an arguably easier algebraic way to do it is to use the fact that, eg, [itex]\hat x = \nabla(x)[/itex], where x is the scalar. spherical coordinates, also called spherical polar coordinates (walton 1967, arfken 1985), are a system of curvilinear coordinates that are natural. i can find a lot of resources that show the inverse, (expressing cylindrical. X Hat In Spherical Coordinates.
From www.slideserve.com
PPT 16.360 Lecture 13 PowerPoint Presentation, free download ID4012508 X Hat In Spherical Coordinates first, $\mathbf{f} = x\mathbf{\hat i} + y\mathbf{\hat j} + z\mathbf{\hat k}$ converted to spherical coordinates is just $\mathbf{f} = \rho. an arguably easier algebraic way to do it is to use the fact that, eg, [itex]\hat x = \nabla(x)[/itex], where x is the scalar. to convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2,. X Hat In Spherical Coordinates.
From mungfali.com
Spherical Coordinates Equations X Hat In Spherical Coordinates spherical coordinates, also called spherical polar coordinates (walton 1967, arfken 1985), are a system of curvilinear coordinates that are natural. \[x = r \sin \theta \cos \phi \] 2. an arguably easier algebraic way to do it is to use the fact that, eg, [itex]\hat x = \nabla(x)[/itex], where x is the scalar. to convert a point. X Hat In Spherical Coordinates.
From www.storyofmathematics.com
Spherical Coordinates Definition, Graph, and Examples X Hat In Spherical Coordinates to convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan θ=\dfrac{y}{x},\) and. an arguably easier algebraic way to do it is to use the fact that, eg, [itex]\hat x = \nabla(x)[/itex], where x is the scalar. spherical coordinates, also called spherical polar coordinates (walton 1967, arfken 1985), are a system of curvilinear coordinates. X Hat In Spherical Coordinates.
From www.youtube.com
Newton's Second Law in Spherical Coordinates Classical Mechanics YouTube X Hat In Spherical Coordinates first, $\mathbf{f} = x\mathbf{\hat i} + y\mathbf{\hat j} + z\mathbf{\hat k}$ converted to spherical coordinates is just $\mathbf{f} = \rho. i can find a lot of resources that show the inverse, (expressing cylindrical in terms of of cartesian) but i just can't find what i want. \[x = r \sin \theta \cos \phi \] 2. spherical coordinates,. X Hat In Spherical Coordinates.
From tikz.net
Differential of Surface Area Spherical Coordinates X Hat In Spherical Coordinates spherical coordinates, also called spherical polar coordinates (walton 1967, arfken 1985), are a system of curvilinear coordinates that are natural. an arguably easier algebraic way to do it is to use the fact that, eg, [itex]\hat x = \nabla(x)[/itex], where x is the scalar. first, $\mathbf{f} = x\mathbf{\hat i} + y\mathbf{\hat j} + z\mathbf{\hat k}$ converted to. X Hat In Spherical Coordinates.
From www.researchgate.net
The spherical coordinates are defined by the polar angle θ 1 [ 0, π ½ Download Scientific X Hat In Spherical Coordinates spherical coordinates, also called spherical polar coordinates (walton 1967, arfken 1985), are a system of curvilinear coordinates that are natural. to convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan θ=\dfrac{y}{x},\) and. i can find a lot of resources that show the inverse, (expressing cylindrical in terms of of cartesian) but i just. X Hat In Spherical Coordinates.
From www.storyofmathematics.com
Spherical Coordinates Definition, Graph, and Examples X Hat In Spherical Coordinates an arguably easier algebraic way to do it is to use the fact that, eg, [itex]\hat x = \nabla(x)[/itex], where x is the scalar. to convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan θ=\dfrac{y}{x},\) and. spherical coordinates, also called spherical polar coordinates (walton 1967, arfken 1985), are a system of curvilinear coordinates. X Hat In Spherical Coordinates.
From chem.libretexts.org
D Spherical Coordinates Chemistry LibreTexts X Hat In Spherical Coordinates i can find a lot of resources that show the inverse, (expressing cylindrical in terms of of cartesian) but i just can't find what i want. spherical coordinates, also called spherical polar coordinates (walton 1967, arfken 1985), are a system of curvilinear coordinates that are natural. \[x = r \sin \theta \cos \phi \] 2. an arguably. X Hat In Spherical Coordinates.
From www.slideserve.com
PPT Spherical coordinates PowerPoint Presentation, free download ID6719151 X Hat In Spherical Coordinates i can find a lot of resources that show the inverse, (expressing cylindrical in terms of of cartesian) but i just can't find what i want. an arguably easier algebraic way to do it is to use the fact that, eg, [itex]\hat x = \nabla(x)[/itex], where x is the scalar. to convert a point from cartesian coordinates. X Hat In Spherical Coordinates.
From www.youtube.com
ECE3300 Lecture 1415 Coordinate Systems Spherical dL YouTube X Hat In Spherical Coordinates \[x = r \sin \theta \cos \phi \] 2. to convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan θ=\dfrac{y}{x},\) and. spherical coordinates, also called spherical polar coordinates (walton 1967, arfken 1985), are a system of curvilinear coordinates that are natural. i can find a lot of resources that show the inverse, (expressing. X Hat In Spherical Coordinates.
From www.researchgate.net
Spherical coordinate system. A point on the hemispherical surface is... Download Scientific X Hat In Spherical Coordinates an arguably easier algebraic way to do it is to use the fact that, eg, [itex]\hat x = \nabla(x)[/itex], where x is the scalar. to convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan θ=\dfrac{y}{x},\) and. first, $\mathbf{f} = x\mathbf{\hat i} + y\mathbf{\hat j} + z\mathbf{\hat k}$ converted to spherical coordinates is just. X Hat In Spherical Coordinates.
From www.youtube.com
Spherical coordinate system YouTube X Hat In Spherical Coordinates first, $\mathbf{f} = x\mathbf{\hat i} + y\mathbf{\hat j} + z\mathbf{\hat k}$ converted to spherical coordinates is just $\mathbf{f} = \rho. spherical coordinates, also called spherical polar coordinates (walton 1967, arfken 1985), are a system of curvilinear coordinates that are natural. to convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan θ=\dfrac{y}{x},\) and. . X Hat In Spherical Coordinates.
From www.chegg.com
Solved Spherical polar coordinates (r, θ, Φ) are defined in X Hat In Spherical Coordinates spherical coordinates, also called spherical polar coordinates (walton 1967, arfken 1985), are a system of curvilinear coordinates that are natural. an arguably easier algebraic way to do it is to use the fact that, eg, [itex]\hat x = \nabla(x)[/itex], where x is the scalar. i can find a lot of resources that show the inverse, (expressing cylindrical. X Hat In Spherical Coordinates.
From www.researchgate.net
Spherical cap coordinate system [38]. Download Scientific Diagram X Hat In Spherical Coordinates an arguably easier algebraic way to do it is to use the fact that, eg, [itex]\hat x = \nabla(x)[/itex], where x is the scalar. i can find a lot of resources that show the inverse, (expressing cylindrical in terms of of cartesian) but i just can't find what i want. first, $\mathbf{f} = x\mathbf{\hat i} + y\mathbf{\hat. X Hat In Spherical Coordinates.
From www.geogebra.org
Spherical Coordinates (robphy) GeoGebra X Hat In Spherical Coordinates first, $\mathbf{f} = x\mathbf{\hat i} + y\mathbf{\hat j} + z\mathbf{\hat k}$ converted to spherical coordinates is just $\mathbf{f} = \rho. i can find a lot of resources that show the inverse, (expressing cylindrical in terms of of cartesian) but i just can't find what i want. an arguably easier algebraic way to do it is to use. X Hat In Spherical Coordinates.
From es.symbolab.com
Study Guide Vectors and the Geometry of Space X Hat In Spherical Coordinates i can find a lot of resources that show the inverse, (expressing cylindrical in terms of of cartesian) but i just can't find what i want. \[x = r \sin \theta \cos \phi \] 2. first, $\mathbf{f} = x\mathbf{\hat i} + y\mathbf{\hat j} + z\mathbf{\hat k}$ converted to spherical coordinates is just $\mathbf{f} = \rho. an arguably. X Hat In Spherical Coordinates.
From math.stackexchange.com
calculus How to find the surface area of a spherical cap by integration? Mathematics Stack X Hat In Spherical Coordinates \[x = r \sin \theta \cos \phi \] 2. spherical coordinates, also called spherical polar coordinates (walton 1967, arfken 1985), are a system of curvilinear coordinates that are natural. first, $\mathbf{f} = x\mathbf{\hat i} + y\mathbf{\hat j} + z\mathbf{\hat k}$ converted to spherical coordinates is just $\mathbf{f} = \rho. to convert a point from cartesian coordinates to. X Hat In Spherical Coordinates.