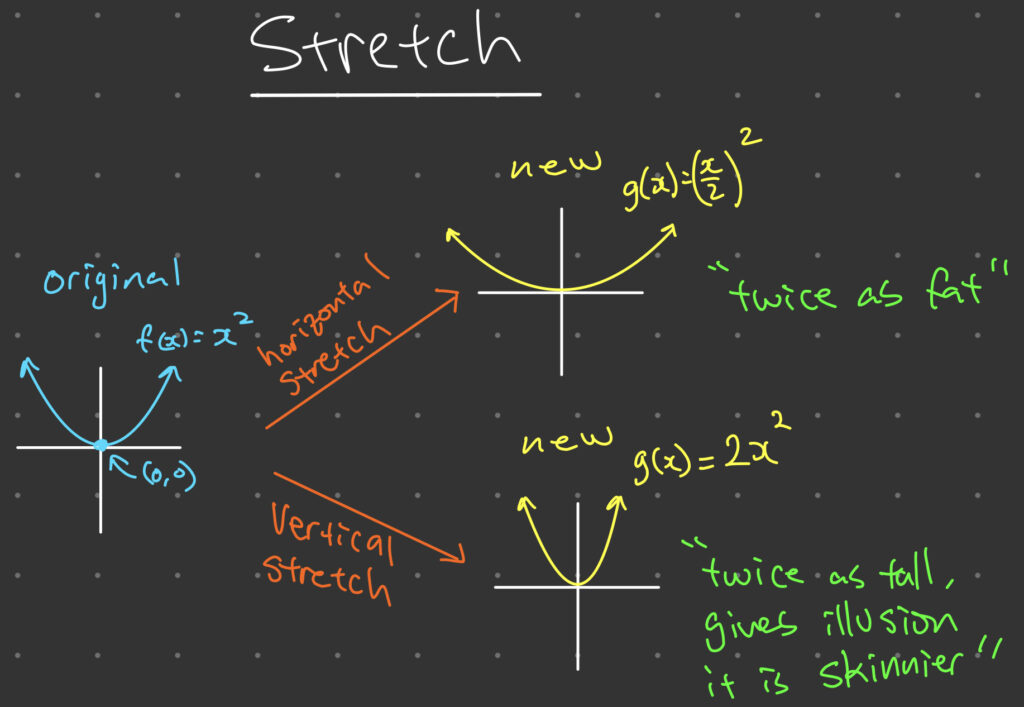
Stretch Vs Compress . If the constant is between 0 and 1, we get a horizontal stretch; H (x) = 1/ (3x) flip it upside down: Here are some things we. If the line becomes flatter, the function has been stretched horizontally or compressed vertically. Stretches and compressions change the slope of a linear function. The function v (x) = x 3 − 4x. Given a function [latex]y=f\left(x\right)[/latex], the form [latex]y=f\left(bx\right)[/latex] results in a horizontal stretch or compression. Figure 1 shows a function multiplied by constant factors 2 and 0.5 and. If the constant is greater than 1, we get a horizontal compression. If the constant is greater than 1, we get a vertical stretch; If the constant is between 0 and 1, we get a vertical compression. Horizontal stretch/compression by a factor of b. If the line becomes steeper, the function has been stretched vertically or compressed horizontally.
from www.easysevens.com
Horizontal stretch/compression by a factor of b. If the constant is between 0 and 1, we get a vertical compression. Stretches and compressions change the slope of a linear function. Here are some things we. The function v (x) = x 3 − 4x. H (x) = 1/ (3x) flip it upside down: If the constant is between 0 and 1, we get a horizontal stretch; If the line becomes steeper, the function has been stretched vertically or compressed horizontally. If the constant is greater than 1, we get a vertical stretch; If the line becomes flatter, the function has been stretched horizontally or compressed vertically.
Transformation of Functions and Graphs Easy Sevens Education
Stretch Vs Compress If the constant is between 0 and 1, we get a vertical compression. If the constant is greater than 1, we get a vertical stretch; If the line becomes flatter, the function has been stretched horizontally or compressed vertically. Figure 1 shows a function multiplied by constant factors 2 and 0.5 and. Here are some things we. H (x) = 1/ (3x) flip it upside down: Given a function [latex]y=f\left(x\right)[/latex], the form [latex]y=f\left(bx\right)[/latex] results in a horizontal stretch or compression. Stretches and compressions change the slope of a linear function. If the line becomes steeper, the function has been stretched vertically or compressed horizontally. If the constant is between 0 and 1, we get a vertical compression. Horizontal stretch/compression by a factor of b. The function v (x) = x 3 − 4x. If the constant is greater than 1, we get a horizontal compression. If the constant is between 0 and 1, we get a horizontal stretch;
From study.com
Stretching & Compressing a Function Video & Lesson Transcript Stretch Vs Compress If the constant is greater than 1, we get a horizontal compression. The function v (x) = x 3 − 4x. Here are some things we. Figure 1 shows a function multiplied by constant factors 2 and 0.5 and. Given a function [latex]y=f\left(x\right)[/latex], the form [latex]y=f\left(bx\right)[/latex] results in a horizontal stretch or compression. If the line becomes steeper, the function. Stretch Vs Compress.
From www.onlinemathlearning.com
Manipulating Graphs Shifts and Stretches (examples, solutions, worksheets, videos, games Stretch Vs Compress Given a function [latex]y=f\left(x\right)[/latex], the form [latex]y=f\left(bx\right)[/latex] results in a horizontal stretch or compression. The function v (x) = x 3 − 4x. If the constant is between 0 and 1, we get a vertical compression. Here are some things we. Stretches and compressions change the slope of a linear function. If the line becomes steeper, the function has been. Stretch Vs Compress.
From www.youtube.com
Math 10 6.4 Graphing Stretches and Compressions YouTube Stretch Vs Compress Horizontal stretch/compression by a factor of b. If the line becomes steeper, the function has been stretched vertically or compressed horizontally. If the constant is greater than 1, we get a vertical stretch; If the constant is between 0 and 1, we get a horizontal stretch; The function v (x) = x 3 − 4x. Given a function [latex]y=f\left(x\right)[/latex], the. Stretch Vs Compress.
From www.youtube.com
Functions Stretching, Compressing, and Reflecting Functions YouTube Stretch Vs Compress If the line becomes steeper, the function has been stretched vertically or compressed horizontally. If the constant is between 0 and 1, we get a horizontal stretch; If the constant is greater than 1, we get a vertical stretch; Stretches and compressions change the slope of a linear function. Figure 1 shows a function multiplied by constant factors 2 and. Stretch Vs Compress.
From www.youtube.com
Transformations Veritcal Stretch Compression YouTube Stretch Vs Compress H (x) = 1/ (3x) flip it upside down: Here are some things we. The function v (x) = x 3 − 4x. Figure 1 shows a function multiplied by constant factors 2 and 0.5 and. If the line becomes flatter, the function has been stretched horizontally or compressed vertically. If the line becomes steeper, the function has been stretched. Stretch Vs Compress.
From www.geogebra.org
Vertical Compressions & Stretches GeoGebra Stretch Vs Compress Horizontal stretch/compression by a factor of b. If the constant is between 0 and 1, we get a vertical compression. If the constant is greater than 1, we get a horizontal compression. Stretches and compressions change the slope of a linear function. Given a function [latex]y=f\left(x\right)[/latex], the form [latex]y=f\left(bx\right)[/latex] results in a horizontal stretch or compression. H (x) = 1/. Stretch Vs Compress.
From www.youtube.com
Determine a Horizontal Stretch or Horizontal Compression YouTube Stretch Vs Compress The function v (x) = x 3 − 4x. If the line becomes flatter, the function has been stretched horizontally or compressed vertically. If the line becomes steeper, the function has been stretched vertically or compressed horizontally. Figure 1 shows a function multiplied by constant factors 2 and 0.5 and. Horizontal stretch/compression by a factor of b. Given a function. Stretch Vs Compress.
From courses.lumenlearning.com
Stretching, Compressing, or Reflecting a Logarithmic Function College Algebra Corequisite Stretch Vs Compress The function v (x) = x 3 − 4x. If the constant is greater than 1, we get a horizontal compression. Given a function [latex]y=f\left(x\right)[/latex], the form [latex]y=f\left(bx\right)[/latex] results in a horizontal stretch or compression. If the line becomes steeper, the function has been stretched vertically or compressed horizontally. H (x) = 1/ (3x) flip it upside down: If the. Stretch Vs Compress.
From www.youtube.com
Ex Identify Horizontal and Vertical Stretches and Compressions Function Notation YouTube Stretch Vs Compress Stretches and compressions change the slope of a linear function. The function v (x) = x 3 − 4x. If the constant is between 0 and 1, we get a horizontal stretch; If the constant is greater than 1, we get a vertical stretch; If the line becomes steeper, the function has been stretched vertically or compressed horizontally. Figure 1. Stretch Vs Compress.
From www.wizeprep.com
Stretches and Compressions Wize Grade 11 Mathematics Textbook Wizeprep Stretch Vs Compress Here are some things we. The function v (x) = x 3 − 4x. If the constant is between 0 and 1, we get a vertical compression. If the constant is greater than 1, we get a horizontal compression. Given a function [latex]y=f\left(x\right)[/latex], the form [latex]y=f\left(bx\right)[/latex] results in a horizontal stretch or compression. Figure 1 shows a function multiplied by. Stretch Vs Compress.
From www.youtube.com
Determinar un estiramiento horizontal o una compresión horizontal YouTube Stretch Vs Compress If the constant is between 0 and 1, we get a vertical compression. The function v (x) = x 3 − 4x. If the constant is greater than 1, we get a horizontal compression. Here are some things we. If the line becomes steeper, the function has been stretched vertically or compressed horizontally. Given a function [latex]y=f\left(x\right)[/latex], the form [latex]y=f\left(bx\right)[/latex]. Stretch Vs Compress.
From www.youtube.com
How to graph a stretch or compression of a quadratic function f(x)=ax^2 Minute Math YouTube Stretch Vs Compress If the constant is between 0 and 1, we get a horizontal stretch; If the line becomes flatter, the function has been stretched horizontally or compressed vertically. Here are some things we. Stretches and compressions change the slope of a linear function. Figure 1 shows a function multiplied by constant factors 2 and 0.5 and. If the constant is between. Stretch Vs Compress.
From www.slideserve.com
PPT 2.7 Absolute Value Functions and Graphs PowerPoint Presentation ID3215397 Stretch Vs Compress Stretches and compressions change the slope of a linear function. H (x) = 1/ (3x) flip it upside down: If the constant is between 0 and 1, we get a horizontal stretch; Figure 1 shows a function multiplied by constant factors 2 and 0.5 and. Here are some things we. Given a function [latex]y=f\left(x\right)[/latex], the form [latex]y=f\left(bx\right)[/latex] results in a. Stretch Vs Compress.
From www.slideserve.com
PPT Transformations of the Parent Functions PowerPoint Presentation ID2166829 Stretch Vs Compress The function v (x) = x 3 − 4x. H (x) = 1/ (3x) flip it upside down: If the constant is between 0 and 1, we get a vertical compression. If the line becomes steeper, the function has been stretched vertically or compressed horizontally. Stretches and compressions change the slope of a linear function. If the constant is greater. Stretch Vs Compress.
From en.neurochispas.com
Stretches and Compressions of Functions with Examples Neurochispas Stretch Vs Compress The function v (x) = x 3 − 4x. If the constant is greater than 1, we get a vertical stretch; If the constant is greater than 1, we get a horizontal compression. Given a function [latex]y=f\left(x\right)[/latex], the form [latex]y=f\left(bx\right)[/latex] results in a horizontal stretch or compression. H (x) = 1/ (3x) flip it upside down: If the line becomes. Stretch Vs Compress.
From www.youtube.com
Horizontal Stretch and Compression YouTube Stretch Vs Compress Figure 1 shows a function multiplied by constant factors 2 and 0.5 and. H (x) = 1/ (3x) flip it upside down: If the constant is greater than 1, we get a horizontal compression. If the constant is between 0 and 1, we get a vertical compression. Horizontal stretch/compression by a factor of b. If the constant is between 0. Stretch Vs Compress.
From www.youtube.com
Determine a Vertical Stretch or Vertical Compression YouTube Stretch Vs Compress If the line becomes flatter, the function has been stretched horizontally or compressed vertically. If the constant is greater than 1, we get a vertical stretch; H (x) = 1/ (3x) flip it upside down: If the constant is greater than 1, we get a horizontal compression. Given a function [latex]y=f\left(x\right)[/latex], the form [latex]y=f\left(bx\right)[/latex] results in a horizontal stretch or. Stretch Vs Compress.
From www.slideserve.com
PPT 44 Periodic Functions; Stretching and Translating Graphs PowerPoint Presentation ID6841990 Stretch Vs Compress H (x) = 1/ (3x) flip it upside down: If the constant is between 0 and 1, we get a horizontal stretch; Given a function [latex]y=f\left(x\right)[/latex], the form [latex]y=f\left(bx\right)[/latex] results in a horizontal stretch or compression. If the constant is between 0 and 1, we get a vertical compression. The function v (x) = x 3 − 4x. Here are. Stretch Vs Compress.
From www.youtube.com
Vertical Stretch and Compression using Absolute Value YouTube Stretch Vs Compress If the constant is between 0 and 1, we get a vertical compression. The function v (x) = x 3 − 4x. If the line becomes flatter, the function has been stretched horizontally or compressed vertically. Here are some things we. H (x) = 1/ (3x) flip it upside down: Given a function [latex]y=f\left(x\right)[/latex], the form [latex]y=f\left(bx\right)[/latex] results in a. Stretch Vs Compress.
From slideplayer.com
HORIZONTAL STRETCHES AND COMPRESSIONS ppt download Stretch Vs Compress Given a function [latex]y=f\left(x\right)[/latex], the form [latex]y=f\left(bx\right)[/latex] results in a horizontal stretch or compression. Stretches and compressions change the slope of a linear function. If the constant is between 0 and 1, we get a vertical compression. If the constant is greater than 1, we get a horizontal compression. If the line becomes flatter, the function has been stretched horizontally. Stretch Vs Compress.
From www.easysevens.com
Transformation of Functions and Graphs Easy Sevens Education Stretch Vs Compress If the line becomes flatter, the function has been stretched horizontally or compressed vertically. Horizontal stretch/compression by a factor of b. The function v (x) = x 3 − 4x. If the constant is greater than 1, we get a horizontal compression. If the constant is between 0 and 1, we get a horizontal stretch; Stretches and compressions change the. Stretch Vs Compress.
From www.emathinstruction.com
Vertical Stretching and Compressing of Functions eMATHinstruction Stretch Vs Compress H (x) = 1/ (3x) flip it upside down: Stretches and compressions change the slope of a linear function. Figure 1 shows a function multiplied by constant factors 2 and 0.5 and. If the constant is greater than 1, we get a horizontal compression. The function v (x) = x 3 − 4x. Given a function [latex]y=f\left(x\right)[/latex], the form [latex]y=f\left(bx\right)[/latex]. Stretch Vs Compress.
From www.youtube.com
Vertical and Horizontal Stretches and Compressions Explained YouTube Stretch Vs Compress Here are some things we. Given a function [latex]y=f\left(x\right)[/latex], the form [latex]y=f\left(bx\right)[/latex] results in a horizontal stretch or compression. H (x) = 1/ (3x) flip it upside down: If the line becomes flatter, the function has been stretched horizontally or compressed vertically. If the constant is greater than 1, we get a vertical stretch; If the constant is between 0. Stretch Vs Compress.
From www.youtube.com
Horizontal and Vertical Stretch and Compression YouTube Stretch Vs Compress Here are some things we. If the constant is between 0 and 1, we get a vertical compression. If the line becomes flatter, the function has been stretched horizontally or compressed vertically. If the constant is greater than 1, we get a horizontal compression. If the constant is greater than 1, we get a vertical stretch; If the constant is. Stretch Vs Compress.
From www.youtube.com
Horizontal Stretch and Compression YouTube Stretch Vs Compress If the constant is between 0 and 1, we get a horizontal stretch; Given a function [latex]y=f\left(x\right)[/latex], the form [latex]y=f\left(bx\right)[/latex] results in a horizontal stretch or compression. If the line becomes steeper, the function has been stretched vertically or compressed horizontally. Figure 1 shows a function multiplied by constant factors 2 and 0.5 and. Horizontal stretch/compression by a factor of. Stretch Vs Compress.
From www.pinterest.com
Vertical Vertical, Compression, Chart Stretch Vs Compress If the line becomes steeper, the function has been stretched vertically or compressed horizontally. Horizontal stretch/compression by a factor of b. If the constant is between 0 and 1, we get a horizontal stretch; Given a function [latex]y=f\left(x\right)[/latex], the form [latex]y=f\left(bx\right)[/latex] results in a horizontal stretch or compression. If the constant is greater than 1, we get a horizontal compression.. Stretch Vs Compress.
From www.youtube.com
Function Transformations Horizontal and Vertical Stretches and Compressions YouTube Stretch Vs Compress If the line becomes steeper, the function has been stretched vertically or compressed horizontally. Figure 1 shows a function multiplied by constant factors 2 and 0.5 and. Here are some things we. H (x) = 1/ (3x) flip it upside down: The function v (x) = x 3 − 4x. Stretches and compressions change the slope of a linear function.. Stretch Vs Compress.
From www.expii.com
Stretch or Compress Function Vertically cf(x) Expii Stretch Vs Compress Here are some things we. If the constant is between 0 and 1, we get a horizontal stretch; If the line becomes flatter, the function has been stretched horizontally or compressed vertically. Stretches and compressions change the slope of a linear function. Figure 1 shows a function multiplied by constant factors 2 and 0.5 and. If the constant is greater. Stretch Vs Compress.
From www.youtube.com
Vertical/Horizontal of Functions YouTube Stretch Vs Compress Stretches and compressions change the slope of a linear function. Figure 1 shows a function multiplied by constant factors 2 and 0.5 and. If the line becomes steeper, the function has been stretched vertically or compressed horizontally. If the constant is greater than 1, we get a horizontal compression. If the constant is greater than 1, we get a vertical. Stretch Vs Compress.
From www.youtube.com
Horizontal Shrink and Stretch Transformations of Linear Functions YouTube Stretch Vs Compress Figure 1 shows a function multiplied by constant factors 2 and 0.5 and. If the constant is greater than 1, we get a vertical stretch; Horizontal stretch/compression by a factor of b. Given a function [latex]y=f\left(x\right)[/latex], the form [latex]y=f\left(bx\right)[/latex] results in a horizontal stretch or compression. If the constant is greater than 1, we get a horizontal compression. If the. Stretch Vs Compress.
From www.youtube.com
Function Transformations Horizontal and Vertical Stretches and Compressions YouTube Stretch Vs Compress Figure 1 shows a function multiplied by constant factors 2 and 0.5 and. If the constant is greater than 1, we get a horizontal compression. Here are some things we. H (x) = 1/ (3x) flip it upside down: If the constant is between 0 and 1, we get a vertical compression. If the line becomes flatter, the function has. Stretch Vs Compress.
From www.teachertube.com
Video Horizontal And Vertical Graph Stretches and Compressions Part 2 Stretch Vs Compress Horizontal stretch/compression by a factor of b. Given a function [latex]y=f\left(x\right)[/latex], the form [latex]y=f\left(bx\right)[/latex] results in a horizontal stretch or compression. If the line becomes flatter, the function has been stretched horizontally or compressed vertically. If the constant is between 0 and 1, we get a vertical compression. Here are some things we. Figure 1 shows a function multiplied by. Stretch Vs Compress.
From www.slideserve.com
PPT Vertical Stretches and Compressions PowerPoint Presentation, free download ID1230376 Stretch Vs Compress Horizontal stretch/compression by a factor of b. Figure 1 shows a function multiplied by constant factors 2 and 0.5 and. If the constant is between 0 and 1, we get a horizontal stretch; Stretches and compressions change the slope of a linear function. If the line becomes steeper, the function has been stretched vertically or compressed horizontally. The function v. Stretch Vs Compress.
From www.slideserve.com
PPT Lecture 12 Elastic Potential Energy & Energy Conservation PowerPoint Presentation ID Stretch Vs Compress The function v (x) = x 3 − 4x. If the line becomes flatter, the function has been stretched horizontally or compressed vertically. H (x) = 1/ (3x) flip it upside down: If the constant is greater than 1, we get a vertical stretch; If the constant is between 0 and 1, we get a vertical compression. Stretches and compressions. Stretch Vs Compress.
From www.geogebra.org
Graphs Stretched vs. Compressed GeoGebra Stretch Vs Compress If the constant is between 0 and 1, we get a horizontal stretch; If the constant is between 0 and 1, we get a vertical compression. Here are some things we. The function v (x) = x 3 − 4x. If the line becomes steeper, the function has been stretched vertically or compressed horizontally. If the constant is greater than. Stretch Vs Compress.