Harmonic Oscillator Angular Frequency . The way around this is to add a coefficient that changes our input variable (time) into something a trig function can handle (radians). It is the number of radians by which the phase. The angular frequency will be a very important quantity in our study of wave phenomena. $\omega_0$ is called the angular frequency; We will almost always denote it by the lower case greek letter, ω (omega). One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. Some of the quantities in have names:
from www.slideserve.com
$\omega_0$ is called the angular frequency; The way around this is to add a coefficient that changes our input variable (time) into something a trig function can handle (radians). Some of the quantities in have names: One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. We will almost always denote it by the lower case greek letter, ω (omega). It is the number of radians by which the phase. The angular frequency will be a very important quantity in our study of wave phenomena.
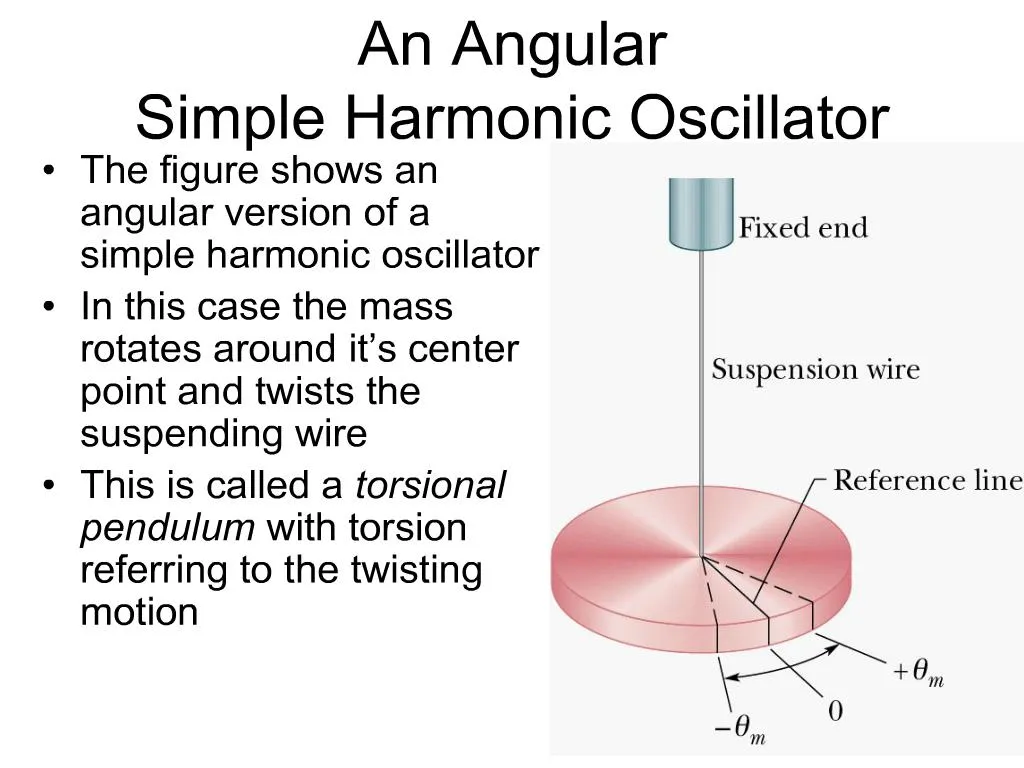
PPT an angular simple harmonic oscillator PowerPoint Presentation, free download ID153534
Harmonic Oscillator Angular Frequency $\omega_0$ is called the angular frequency; The angular frequency will be a very important quantity in our study of wave phenomena. The way around this is to add a coefficient that changes our input variable (time) into something a trig function can handle (radians). One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. We will almost always denote it by the lower case greek letter, ω (omega). It is the number of radians by which the phase. Some of the quantities in have names: $\omega_0$ is called the angular frequency;
From www.tessshebaylo.com
Angular Frequency Equation Tessshebaylo Harmonic Oscillator Angular Frequency We will almost always denote it by the lower case greek letter, ω (omega). The way around this is to add a coefficient that changes our input variable (time) into something a trig function can handle (radians). The angular frequency will be a very important quantity in our study of wave phenomena. It is the number of radians by which. Harmonic Oscillator Angular Frequency.
From www.chegg.com
Solved A harmonic oscillator has angular frequency w and Harmonic Oscillator Angular Frequency It is the number of radians by which the phase. The way around this is to add a coefficient that changes our input variable (time) into something a trig function can handle (radians). We will almost always denote it by the lower case greek letter, ω (omega). $\omega_0$ is called the angular frequency; One of the most important examples of. Harmonic Oscillator Angular Frequency.
From www.chegg.com
Solved A harmonic oscillator has angular frequency w and Harmonic Oscillator Angular Frequency One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. Some of the quantities in have names: The way around this is to add a coefficient that changes our input variable (time) into something a trig function can handle (radians). The angular frequency will be a very important quantity. Harmonic Oscillator Angular Frequency.
From www.youtube.com
Simple Harmonic Motion Period and Frequency YouTube Harmonic Oscillator Angular Frequency One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. The way around this is to add a coefficient that changes our input variable (time) into something a trig function can handle (radians). Some of the quantities in have names: $\omega_0$ is called the angular frequency; We will almost. Harmonic Oscillator Angular Frequency.
From www.numerade.com
SOLVED A harmonic oscillator has angular frequency ω and amplitude A. (a) What are the Harmonic Oscillator Angular Frequency We will almost always denote it by the lower case greek letter, ω (omega). $\omega_0$ is called the angular frequency; Some of the quantities in have names: The angular frequency will be a very important quantity in our study of wave phenomena. The way around this is to add a coefficient that changes our input variable (time) into something a. Harmonic Oscillator Angular Frequency.
From www.chegg.com
Solved A harmonic oscillator Hamiltonian of angular Harmonic Oscillator Angular Frequency One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. It is the number of radians by which the phase. We will almost always denote it by the lower case greek letter, ω (omega). The angular frequency will be a very important quantity in our study of wave phenomena.. Harmonic Oscillator Angular Frequency.
From kunduz.com
[ANSWERED] 12 A simple harmonic oscillator of angular frequency 2 rad s Kunduz Harmonic Oscillator Angular Frequency Some of the quantities in have names: The way around this is to add a coefficient that changes our input variable (time) into something a trig function can handle (radians). The angular frequency will be a very important quantity in our study of wave phenomena. One of the most important examples of periodic motion is simple harmonic motion (shm), in. Harmonic Oscillator Angular Frequency.
From universe-review.ca
Harmonic Oscillator Harmonic Oscillator Angular Frequency $\omega_0$ is called the angular frequency; It is the number of radians by which the phase. The way around this is to add a coefficient that changes our input variable (time) into something a trig function can handle (radians). The angular frequency will be a very important quantity in our study of wave phenomena. Some of the quantities in have. Harmonic Oscillator Angular Frequency.
From www.chegg.com
Solved A harmonic oscillator has angular frequency w and Harmonic Oscillator Angular Frequency $\omega_0$ is called the angular frequency; Some of the quantities in have names: One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. The angular frequency will be a very important quantity in our study of wave phenomena. It is the number of radians by which the phase. The. Harmonic Oscillator Angular Frequency.
From favpng.com
Damping Ratio Oscillation Harmonic Oscillator Angular Frequency Force, PNG, 548x514px, Damping Harmonic Oscillator Angular Frequency One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. The angular frequency will be a very important quantity in our study of wave phenomena. Some of the quantities in have names: It is the number of radians by which the phase. The way around this is to add. Harmonic Oscillator Angular Frequency.
From www.slideserve.com
PPT an angular simple harmonic oscillator PowerPoint Presentation, free download ID153534 Harmonic Oscillator Angular Frequency Some of the quantities in have names: The angular frequency will be a very important quantity in our study of wave phenomena. One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. It is the number of radians by which the phase. The way around this is to add. Harmonic Oscillator Angular Frequency.
From byjus.com
A light damped oscillator with the frequency (ω) is set in motion by harmonic driving force of Harmonic Oscillator Angular Frequency $\omega_0$ is called the angular frequency; The angular frequency will be a very important quantity in our study of wave phenomena. Some of the quantities in have names: One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. It is the number of radians by which the phase. We. Harmonic Oscillator Angular Frequency.
From www.toppr.com
A simple harmonic oscillator of angular frequency 2 rad s is acted upon by an external force F Harmonic Oscillator Angular Frequency We will almost always denote it by the lower case greek letter, ω (omega). One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. The angular frequency will be a very important quantity in our study of wave phenomena. $\omega_0$ is called the angular frequency; The way around this. Harmonic Oscillator Angular Frequency.
From edurev.in
Consider a one dimensional harmonic oscillator of angular frequency andomega;. If 5 identical Harmonic Oscillator Angular Frequency One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. The way around this is to add a coefficient that changes our input variable (time) into something a trig function can handle (radians). Some of the quantities in have names: $\omega_0$ is called the angular frequency; The angular frequency. Harmonic Oscillator Angular Frequency.
From www.toppr.com
A simple harmonic oscillator of angular frequency 2 rad s^1 is acted upon by an external force Harmonic Oscillator Angular Frequency One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. Some of the quantities in have names: We will almost always denote it by the lower case greek letter, ω (omega). It is the number of radians by which the phase. The way around this is to add a. Harmonic Oscillator Angular Frequency.
From slideplayer.com
Chapter 15 Oscillations ppt download Harmonic Oscillator Angular Frequency Some of the quantities in have names: One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. The angular frequency will be a very important quantity in our study of wave phenomena. We will almost always denote it by the lower case greek letter, ω (omega). The way around. Harmonic Oscillator Angular Frequency.
From scoop.eduncle.com
Consider a onedimensional harmonic oscillator of angular frequency w. Harmonic Oscillator Angular Frequency The way around this is to add a coefficient that changes our input variable (time) into something a trig function can handle (radians). We will almost always denote it by the lower case greek letter, ω (omega). The angular frequency will be a very important quantity in our study of wave phenomena. $\omega_0$ is called the angular frequency; It is. Harmonic Oscillator Angular Frequency.
From en.ppt-online.org
Oscillatory motion. Simple harmonic motion. The simple pendulum. Damped harmonic oscillations Harmonic Oscillator Angular Frequency It is the number of radians by which the phase. One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. We will almost always denote it by the lower case greek letter, ω (omega). Some of the quantities in have names: The way around this is to add a. Harmonic Oscillator Angular Frequency.
From www.meritnation.com
In a simple harmonic oscillator of angular frequency 2 rad/s is acted upon by an external force Harmonic Oscillator Angular Frequency The way around this is to add a coefficient that changes our input variable (time) into something a trig function can handle (radians). The angular frequency will be a very important quantity in our study of wave phenomena. $\omega_0$ is called the angular frequency; We will almost always denote it by the lower case greek letter, ω (omega). It is. Harmonic Oscillator Angular Frequency.
From www.chegg.com
Solved Two harmonic oscillators have the same angular Harmonic Oscillator Angular Frequency We will almost always denote it by the lower case greek letter, ω (omega). $\omega_0$ is called the angular frequency; One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. Some of the quantities in have names: The angular frequency will be a very important quantity in our study. Harmonic Oscillator Angular Frequency.
From en.ppt-online.org
Oscillatory motion. Simple harmonic motion. The simple pendulum. Damped harmonic oscillations Harmonic Oscillator Angular Frequency One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. The way around this is to add a coefficient that changes our input variable (time) into something a trig function can handle (radians). Some of the quantities in have names: $\omega_0$ is called the angular frequency; It is the. Harmonic Oscillator Angular Frequency.
From www.numerade.com
SOLVEDA harmonic oscillator of angular frequency 2 s^1 is initially at x= 3 m, with ẋ=8 m s Harmonic Oscillator Angular Frequency The angular frequency will be a very important quantity in our study of wave phenomena. We will almost always denote it by the lower case greek letter, ω (omega). The way around this is to add a coefficient that changes our input variable (time) into something a trig function can handle (radians). $\omega_0$ is called the angular frequency; Some of. Harmonic Oscillator Angular Frequency.
From tikz.net
Harmonic Oscillator Energy vs. Angular Frequency Harmonic Oscillator Angular Frequency It is the number of radians by which the phase. We will almost always denote it by the lower case greek letter, ω (omega). $\omega_0$ is called the angular frequency; One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. The way around this is to add a coefficient. Harmonic Oscillator Angular Frequency.
From www.tessshebaylo.com
Angular Frequency Equation Oscillation Tessshebaylo Harmonic Oscillator Angular Frequency $\omega_0$ is called the angular frequency; One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. We will almost always denote it by the lower case greek letter, ω (omega). Some of the quantities in have names: The angular frequency will be a very important quantity in our study. Harmonic Oscillator Angular Frequency.
From znanio.ru
Oscillations Harmonic Oscillator Angular Frequency The angular frequency will be a very important quantity in our study of wave phenomena. We will almost always denote it by the lower case greek letter, ω (omega). The way around this is to add a coefficient that changes our input variable (time) into something a trig function can handle (radians). One of the most important examples of periodic. Harmonic Oscillator Angular Frequency.
From www.youtube.com
Energy in Simple Harmonic Oscillators YouTube Harmonic Oscillator Angular Frequency We will almost always denote it by the lower case greek letter, ω (omega). The angular frequency will be a very important quantity in our study of wave phenomena. Some of the quantities in have names: $\omega_0$ is called the angular frequency; One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical. Harmonic Oscillator Angular Frequency.
From imgbin.com
Damping Ratio Oscillation Harmonic Oscillator Angular Frequency Force PNG, Clipart, Amplitude Harmonic Oscillator Angular Frequency The angular frequency will be a very important quantity in our study of wave phenomena. We will almost always denote it by the lower case greek letter, ω (omega). One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. $\omega_0$ is called the angular frequency; It is the number. Harmonic Oscillator Angular Frequency.
From www.chegg.com
Solved 1. Consider a harmonic oscillator of mass m and Harmonic Oscillator Angular Frequency The way around this is to add a coefficient that changes our input variable (time) into something a trig function can handle (radians). We will almost always denote it by the lower case greek letter, ω (omega). It is the number of radians by which the phase. Some of the quantities in have names: One of the most important examples. Harmonic Oscillator Angular Frequency.
From www.youtube.com
Simple Harmonic Motion (15 of 16) Amplitude, Period & Frequency YouTube Harmonic Oscillator Angular Frequency One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. Some of the quantities in have names: It is the number of radians by which the phase. The angular frequency will be a very important quantity in our study of wave phenomena. The way around this is to add. Harmonic Oscillator Angular Frequency.
From www.toppr.com
A simple harmonic oscillator of angular frequency 2 rads is acted upon by an external force F Harmonic Oscillator Angular Frequency Some of the quantities in have names: The way around this is to add a coefficient that changes our input variable (time) into something a trig function can handle (radians). The angular frequency will be a very important quantity in our study of wave phenomena. $\omega_0$ is called the angular frequency; We will almost always denote it by the lower. Harmonic Oscillator Angular Frequency.
From www.toppr.com
The equation of a damped simple harmonic motion is md^2x/dt^2 + bdx/dt + kx = 0 . Then the Harmonic Oscillator Angular Frequency $\omega_0$ is called the angular frequency; The angular frequency will be a very important quantity in our study of wave phenomena. It is the number of radians by which the phase. The way around this is to add a coefficient that changes our input variable (time) into something a trig function can handle (radians). We will almost always denote it. Harmonic Oscillator Angular Frequency.
From www.toppr.com
Two bodies of masses 1 kg and 4 kg are connected to a vertical spring, as shown in the figure Harmonic Oscillator Angular Frequency $\omega_0$ is called the angular frequency; Some of the quantities in have names: The way around this is to add a coefficient that changes our input variable (time) into something a trig function can handle (radians). We will almost always denote it by the lower case greek letter, ω (omega). One of the most important examples of periodic motion is. Harmonic Oscillator Angular Frequency.
From www.slideserve.com
PPT Chapter 14 Oscillations PowerPoint Presentation, free download ID3118391 Harmonic Oscillator Angular Frequency $\omega_0$ is called the angular frequency; Some of the quantities in have names: The angular frequency will be a very important quantity in our study of wave phenomena. One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. We will almost always denote it by the lower case greek. Harmonic Oscillator Angular Frequency.
From www.slideserve.com
PPT Unit 6 Lesson 1 Simple Harmonic Motion SHM PowerPoint Presentation ID2194225 Harmonic Oscillator Angular Frequency One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. It is the number of radians by which the phase. Some of the quantities in have names: The angular frequency will be a very important quantity in our study of wave phenomena. $\omega_0$ is called the angular frequency; We. Harmonic Oscillator Angular Frequency.
From www.slideshare.net
Physics Chapter 9Simple Harmonic Motion Harmonic Oscillator Angular Frequency One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. $\omega_0$ is called the angular frequency; Some of the quantities in have names: It is the number of radians by which the phase. The angular frequency will be a very important quantity in our study of wave phenomena. The. Harmonic Oscillator Angular Frequency.