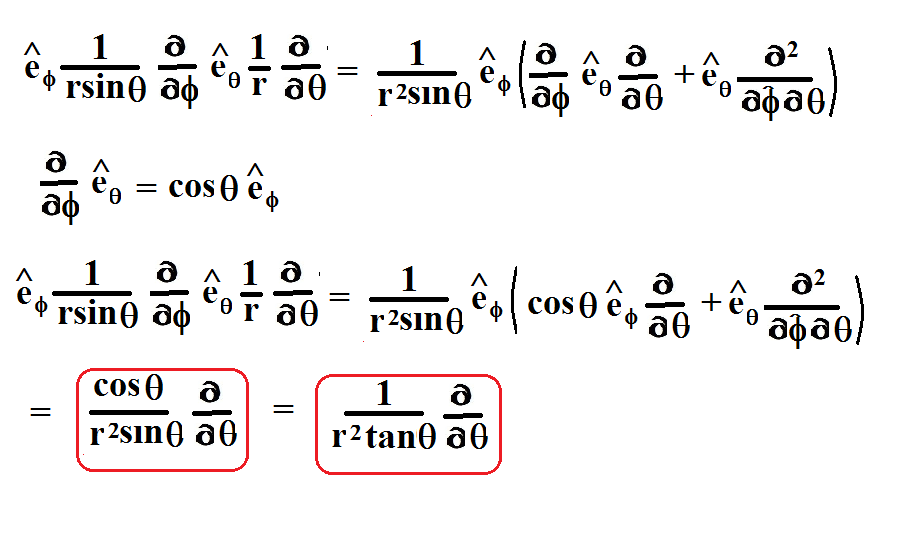Cylindrical Laplacian . In this final section we will establish some relationships between the gradient, divergence and curl, and we will also introduce a new. Solutions to the laplace equation in cylindrical coordinates have wide applicability from fluid mechanics to electrostatics. The most obvious potential strategy is to just apply the laplacian. The laplacian relates the electric potential (i.e., \(v\), units of v) to electric charge density (i.e., \(\rho_v\), units of c/m\(^3\)). Beginning with the laplacian in cylindrical coordinates, apply the operator to a potential function and set it equal to zero to get. Note that we have selected exponential, rather than oscillating, solutions in the. Let’s try this a different way. I want to derive the laplacian for cylindrical polar coordinates, directly, not using the explicit formula for the laplacian for curvilinear coordinates. In cylindrical coordinates, laplace's equation is written.
from gmjacksonphysics.blogspot.com
In this final section we will establish some relationships between the gradient, divergence and curl, and we will also introduce a new. Let’s try this a different way. Solutions to the laplace equation in cylindrical coordinates have wide applicability from fluid mechanics to electrostatics. Note that we have selected exponential, rather than oscillating, solutions in the. Beginning with the laplacian in cylindrical coordinates, apply the operator to a potential function and set it equal to zero to get. In cylindrical coordinates, laplace's equation is written. The most obvious potential strategy is to just apply the laplacian. I want to derive the laplacian for cylindrical polar coordinates, directly, not using the explicit formula for the laplacian for curvilinear coordinates. The laplacian relates the electric potential (i.e., \(v\), units of v) to electric charge density (i.e., \(\rho_v\), units of c/m\(^3\)).
GM Jackson Physics and Mathematics How to Derive the Laplace Operator
Cylindrical Laplacian Let’s try this a different way. In this final section we will establish some relationships between the gradient, divergence and curl, and we will also introduce a new. Let’s try this a different way. In cylindrical coordinates, laplace's equation is written. The most obvious potential strategy is to just apply the laplacian. Beginning with the laplacian in cylindrical coordinates, apply the operator to a potential function and set it equal to zero to get. Solutions to the laplace equation in cylindrical coordinates have wide applicability from fluid mechanics to electrostatics. I want to derive the laplacian for cylindrical polar coordinates, directly, not using the explicit formula for the laplacian for curvilinear coordinates. The laplacian relates the electric potential (i.e., \(v\), units of v) to electric charge density (i.e., \(\rho_v\), units of c/m\(^3\)). Note that we have selected exponential, rather than oscillating, solutions in the.
From www.youtube.com
The Laplacian In Cylindrical Coordinates YouTube Cylindrical Laplacian Solutions to the laplace equation in cylindrical coordinates have wide applicability from fluid mechanics to electrostatics. In cylindrical coordinates, laplace's equation is written. Beginning with the laplacian in cylindrical coordinates, apply the operator to a potential function and set it equal to zero to get. Note that we have selected exponential, rather than oscillating, solutions in the. Let’s try this. Cylindrical Laplacian.
From newbedev.com
Solve Laplace equation in Cylindrical Polar Coordinates Cylindrical Laplacian Beginning with the laplacian in cylindrical coordinates, apply the operator to a potential function and set it equal to zero to get. In cylindrical coordinates, laplace's equation is written. Solutions to the laplace equation in cylindrical coordinates have wide applicability from fluid mechanics to electrostatics. The laplacian relates the electric potential (i.e., \(v\), units of v) to electric charge density. Cylindrical Laplacian.
From www.youtube.com
Laplacian In Cylindrical Coordinates From One Tensor Boi YouTube Cylindrical Laplacian Let’s try this a different way. Note that we have selected exponential, rather than oscillating, solutions in the. I want to derive the laplacian for cylindrical polar coordinates, directly, not using the explicit formula for the laplacian for curvilinear coordinates. Beginning with the laplacian in cylindrical coordinates, apply the operator to a potential function and set it equal to zero. Cylindrical Laplacian.
From www.academia.edu
(PDF) Laplace's Equation in Cylindrical Coordinates and Bessel's Cylindrical Laplacian In cylindrical coordinates, laplace's equation is written. Beginning with the laplacian in cylindrical coordinates, apply the operator to a potential function and set it equal to zero to get. The most obvious potential strategy is to just apply the laplacian. Note that we have selected exponential, rather than oscillating, solutions in the. The laplacian relates the electric potential (i.e., \(v\),. Cylindrical Laplacian.
From www.youtube.com
Laplace's Equation In Cylindrical Coordinates (Part1) (Hindi) YouTube Cylindrical Laplacian I want to derive the laplacian for cylindrical polar coordinates, directly, not using the explicit formula for the laplacian for curvilinear coordinates. Solutions to the laplace equation in cylindrical coordinates have wide applicability from fluid mechanics to electrostatics. Beginning with the laplacian in cylindrical coordinates, apply the operator to a potential function and set it equal to zero to get.. Cylindrical Laplacian.
From www.youtube.com
Laplacian of a vector 1)cylindrical 2)spherical Tensor analysis M.Sc Cylindrical Laplacian Let’s try this a different way. I want to derive the laplacian for cylindrical polar coordinates, directly, not using the explicit formula for the laplacian for curvilinear coordinates. Solutions to the laplace equation in cylindrical coordinates have wide applicability from fluid mechanics to electrostatics. In cylindrical coordinates, laplace's equation is written. The laplacian relates the electric potential (i.e., \(v\), units. Cylindrical Laplacian.
From medium.com
Understanding the Laplacian and the Harmonic Functions by Panos Cylindrical Laplacian In cylindrical coordinates, laplace's equation is written. Note that we have selected exponential, rather than oscillating, solutions in the. I want to derive the laplacian for cylindrical polar coordinates, directly, not using the explicit formula for the laplacian for curvilinear coordinates. Solutions to the laplace equation in cylindrical coordinates have wide applicability from fluid mechanics to electrostatics. The laplacian relates. Cylindrical Laplacian.
From newbedev.com
Solve Laplace equation in Cylindrical Polar Coordinates Cylindrical Laplacian The laplacian relates the electric potential (i.e., \(v\), units of v) to electric charge density (i.e., \(\rho_v\), units of c/m\(^3\)). In this final section we will establish some relationships between the gradient, divergence and curl, and we will also introduce a new. Beginning with the laplacian in cylindrical coordinates, apply the operator to a potential function and set it equal. Cylindrical Laplacian.
From www.studypool.com
SOLUTION Laplacian in plane cylindrical and spherical coordinates Cylindrical Laplacian The laplacian relates the electric potential (i.e., \(v\), units of v) to electric charge density (i.e., \(\rho_v\), units of c/m\(^3\)). In this final section we will establish some relationships between the gradient, divergence and curl, and we will also introduce a new. Note that we have selected exponential, rather than oscillating, solutions in the. In cylindrical coordinates, laplace's equation is. Cylindrical Laplacian.
From www.youtube.com
lecture17 The Laplacian in Cylindrical Coordinates YouTube Cylindrical Laplacian In cylindrical coordinates, laplace's equation is written. Note that we have selected exponential, rather than oscillating, solutions in the. I want to derive the laplacian for cylindrical polar coordinates, directly, not using the explicit formula for the laplacian for curvilinear coordinates. The laplacian relates the electric potential (i.e., \(v\), units of v) to electric charge density (i.e., \(\rho_v\), units of. Cylindrical Laplacian.
From www.youtube.com
Laplacian cylindrical part2 YouTube Cylindrical Laplacian In cylindrical coordinates, laplace's equation is written. I want to derive the laplacian for cylindrical polar coordinates, directly, not using the explicit formula for the laplacian for curvilinear coordinates. Beginning with the laplacian in cylindrical coordinates, apply the operator to a potential function and set it equal to zero to get. The most obvious potential strategy is to just apply. Cylindrical Laplacian.
From www.studypool.com
SOLUTION Laplacian in plane cylindrical and spherical coordinates Cylindrical Laplacian Let’s try this a different way. Solutions to the laplace equation in cylindrical coordinates have wide applicability from fluid mechanics to electrostatics. The most obvious potential strategy is to just apply the laplacian. I want to derive the laplacian for cylindrical polar coordinates, directly, not using the explicit formula for the laplacian for curvilinear coordinates. Note that we have selected. Cylindrical Laplacian.
From gmjacksonphysics.blogspot.com
GM Jackson Physics and Mathematics How to Derive the Laplace Operator Cylindrical Laplacian Note that we have selected exponential, rather than oscillating, solutions in the. The most obvious potential strategy is to just apply the laplacian. In cylindrical coordinates, laplace's equation is written. Let’s try this a different way. I want to derive the laplacian for cylindrical polar coordinates, directly, not using the explicit formula for the laplacian for curvilinear coordinates. Beginning with. Cylindrical Laplacian.
From www.chegg.com
In cylindrical coordinates, (ρ,ϕ,z), the Laplacian is Cylindrical Laplacian The most obvious potential strategy is to just apply the laplacian. In cylindrical coordinates, laplace's equation is written. In this final section we will establish some relationships between the gradient, divergence and curl, and we will also introduce a new. Let’s try this a different way. The laplacian relates the electric potential (i.e., \(v\), units of v) to electric charge. Cylindrical Laplacian.
From www.youtube.com
Differential forms calculation the Laplacian in spherical, cylindrical Cylindrical Laplacian I want to derive the laplacian for cylindrical polar coordinates, directly, not using the explicit formula for the laplacian for curvilinear coordinates. Note that we have selected exponential, rather than oscillating, solutions in the. The most obvious potential strategy is to just apply the laplacian. Beginning with the laplacian in cylindrical coordinates, apply the operator to a potential function and. Cylindrical Laplacian.
From www.chegg.com
Solved Laplace's in Cylindrical Coordinates is shown on page Cylindrical Laplacian Solutions to the laplace equation in cylindrical coordinates have wide applicability from fluid mechanics to electrostatics. Note that we have selected exponential, rather than oscillating, solutions in the. Beginning with the laplacian in cylindrical coordinates, apply the operator to a potential function and set it equal to zero to get. The laplacian relates the electric potential (i.e., \(v\), units of. Cylindrical Laplacian.
From www.chegg.com
Solved 2. In cylindrical coordinates the Laplace equation Cylindrical Laplacian Solutions to the laplace equation in cylindrical coordinates have wide applicability from fluid mechanics to electrostatics. The most obvious potential strategy is to just apply the laplacian. In this final section we will establish some relationships between the gradient, divergence and curl, and we will also introduce a new. Beginning with the laplacian in cylindrical coordinates, apply the operator to. Cylindrical Laplacian.
From www.youtube.com
Laplace equation in all coordinates YouTube Cylindrical Laplacian The laplacian relates the electric potential (i.e., \(v\), units of v) to electric charge density (i.e., \(\rho_v\), units of c/m\(^3\)). In this final section we will establish some relationships between the gradient, divergence and curl, and we will also introduce a new. Beginning with the laplacian in cylindrical coordinates, apply the operator to a potential function and set it equal. Cylindrical Laplacian.
From www.youtube.com
Laplacian in cylindrical coordinate part3 YouTube Cylindrical Laplacian Let’s try this a different way. I want to derive the laplacian for cylindrical polar coordinates, directly, not using the explicit formula for the laplacian for curvilinear coordinates. The laplacian relates the electric potential (i.e., \(v\), units of v) to electric charge density (i.e., \(\rho_v\), units of c/m\(^3\)). Beginning with the laplacian in cylindrical coordinates, apply the operator to a. Cylindrical Laplacian.
From gmjacksonphysics.blogspot.com
GM Jackson Physics and Mathematics How to Derive the Laplace Operator Cylindrical Laplacian The laplacian relates the electric potential (i.e., \(v\), units of v) to electric charge density (i.e., \(\rho_v\), units of c/m\(^3\)). Beginning with the laplacian in cylindrical coordinates, apply the operator to a potential function and set it equal to zero to get. Note that we have selected exponential, rather than oscillating, solutions in the. Let’s try this a different way.. Cylindrical Laplacian.
From www.slideserve.com
PPT Lecture 12 PowerPoint Presentation, free download ID519846 Cylindrical Laplacian The most obvious potential strategy is to just apply the laplacian. Solutions to the laplace equation in cylindrical coordinates have wide applicability from fluid mechanics to electrostatics. In this final section we will establish some relationships between the gradient, divergence and curl, and we will also introduce a new. In cylindrical coordinates, laplace's equation is written. The laplacian relates the. Cylindrical Laplacian.
From gmjacksonphysics.blogspot.com
GM Jackson Physics and Mathematics How to Derive the Laplace Operator Cylindrical Laplacian Beginning with the laplacian in cylindrical coordinates, apply the operator to a potential function and set it equal to zero to get. I want to derive the laplacian for cylindrical polar coordinates, directly, not using the explicit formula for the laplacian for curvilinear coordinates. Note that we have selected exponential, rather than oscillating, solutions in the. In cylindrical coordinates, laplace's. Cylindrical Laplacian.
From www.coursehero.com
[Solved] . Exercise 24 Derive the 3D Laplacian operator in cylindrical Cylindrical Laplacian Beginning with the laplacian in cylindrical coordinates, apply the operator to a potential function and set it equal to zero to get. In this final section we will establish some relationships between the gradient, divergence and curl, and we will also introduce a new. The laplacian relates the electric potential (i.e., \(v\), units of v) to electric charge density (i.e.,. Cylindrical Laplacian.
From www.youtube.com
Laplace's Equation In Cylindrical Coordinates (Part2) (Hindi) YouTube Cylindrical Laplacian In this final section we will establish some relationships between the gradient, divergence and curl, and we will also introduce a new. Let’s try this a different way. In cylindrical coordinates, laplace's equation is written. I want to derive the laplacian for cylindrical polar coordinates, directly, not using the explicit formula for the laplacian for curvilinear coordinates. The most obvious. Cylindrical Laplacian.
From www.youtube.com
Cylindrical capacitor Applications of Laplace's equation for Cylindrical Laplacian In cylindrical coordinates, laplace's equation is written. Beginning with the laplacian in cylindrical coordinates, apply the operator to a potential function and set it equal to zero to get. Solutions to the laplace equation in cylindrical coordinates have wide applicability from fluid mechanics to electrostatics. Let’s try this a different way. I want to derive the laplacian for cylindrical polar. Cylindrical Laplacian.
From www.slideserve.com
PPT Capacitance and Laplace’s Equation PowerPoint Presentation, free Cylindrical Laplacian Solutions to the laplace equation in cylindrical coordinates have wide applicability from fluid mechanics to electrostatics. Let’s try this a different way. Beginning with the laplacian in cylindrical coordinates, apply the operator to a potential function and set it equal to zero to get. Note that we have selected exponential, rather than oscillating, solutions in the. The most obvious potential. Cylindrical Laplacian.
From www.youtube.com
PHYS 2500 Lec 26a Laplacian in Cylindrical Polar coordinates Bessel Cylindrical Laplacian Solutions to the laplace equation in cylindrical coordinates have wide applicability from fluid mechanics to electrostatics. In this final section we will establish some relationships between the gradient, divergence and curl, and we will also introduce a new. I want to derive the laplacian for cylindrical polar coordinates, directly, not using the explicit formula for the laplacian for curvilinear coordinates.. Cylindrical Laplacian.
From studylib.net
Separation of Variables in Laplace`s Equation in Cylindrical Cylindrical Laplacian Note that we have selected exponential, rather than oscillating, solutions in the. The laplacian relates the electric potential (i.e., \(v\), units of v) to electric charge density (i.e., \(\rho_v\), units of c/m\(^3\)). The most obvious potential strategy is to just apply the laplacian. I want to derive the laplacian for cylindrical polar coordinates, directly, not using the explicit formula for. Cylindrical Laplacian.
From www.phys.ksu.edu
Electrodynamics I, KSU Physics Cylindrical Laplacian Note that we have selected exponential, rather than oscillating, solutions in the. The most obvious potential strategy is to just apply the laplacian. In this final section we will establish some relationships between the gradient, divergence and curl, and we will also introduce a new. I want to derive the laplacian for cylindrical polar coordinates, directly, not using the explicit. Cylindrical Laplacian.
From www.slideserve.com
PPT CHAPTER 20 LAPLACE EQUATION PowerPoint Presentation, free Cylindrical Laplacian Beginning with the laplacian in cylindrical coordinates, apply the operator to a potential function and set it equal to zero to get. In cylindrical coordinates, laplace's equation is written. Note that we have selected exponential, rather than oscillating, solutions in the. Solutions to the laplace equation in cylindrical coordinates have wide applicability from fluid mechanics to electrostatics. The most obvious. Cylindrical Laplacian.
From gmjacksonphysics.blogspot.com
GM Jackson Physics and Mathematics How to Derive the Laplace Operator Cylindrical Laplacian Note that we have selected exponential, rather than oscillating, solutions in the. Solutions to the laplace equation in cylindrical coordinates have wide applicability from fluid mechanics to electrostatics. In this final section we will establish some relationships between the gradient, divergence and curl, and we will also introduce a new. I want to derive the laplacian for cylindrical polar coordinates,. Cylindrical Laplacian.
From www.youtube.com
VP9 Laplace Cylindrical YouTube Cylindrical Laplacian Let’s try this a different way. Beginning with the laplacian in cylindrical coordinates, apply the operator to a potential function and set it equal to zero to get. In cylindrical coordinates, laplace's equation is written. Note that we have selected exponential, rather than oscillating, solutions in the. Solutions to the laplace equation in cylindrical coordinates have wide applicability from fluid. Cylindrical Laplacian.
From www.slideserve.com
PPT CHAPTER 20 LAPLACE EQUATION PowerPoint Presentation, free Cylindrical Laplacian The laplacian relates the electric potential (i.e., \(v\), units of v) to electric charge density (i.e., \(\rho_v\), units of c/m\(^3\)). In cylindrical coordinates, laplace's equation is written. Solutions to the laplace equation in cylindrical coordinates have wide applicability from fluid mechanics to electrostatics. The most obvious potential strategy is to just apply the laplacian. Note that we have selected exponential,. Cylindrical Laplacian.
From www.youtube.com
ECE221 Laplace's Equation and Poisson's Equation YouTube Cylindrical Laplacian In cylindrical coordinates, laplace's equation is written. In this final section we will establish some relationships between the gradient, divergence and curl, and we will also introduce a new. The most obvious potential strategy is to just apply the laplacian. Let’s try this a different way. Note that we have selected exponential, rather than oscillating, solutions in the. The laplacian. Cylindrical Laplacian.
From www.chegg.com
3.6 Laplace's Equation in Cylindrical Coordinates; Cylindrical Laplacian In this final section we will establish some relationships between the gradient, divergence and curl, and we will also introduce a new. Let’s try this a different way. The laplacian relates the electric potential (i.e., \(v\), units of v) to electric charge density (i.e., \(\rho_v\), units of c/m\(^3\)). The most obvious potential strategy is to just apply the laplacian. In. Cylindrical Laplacian.