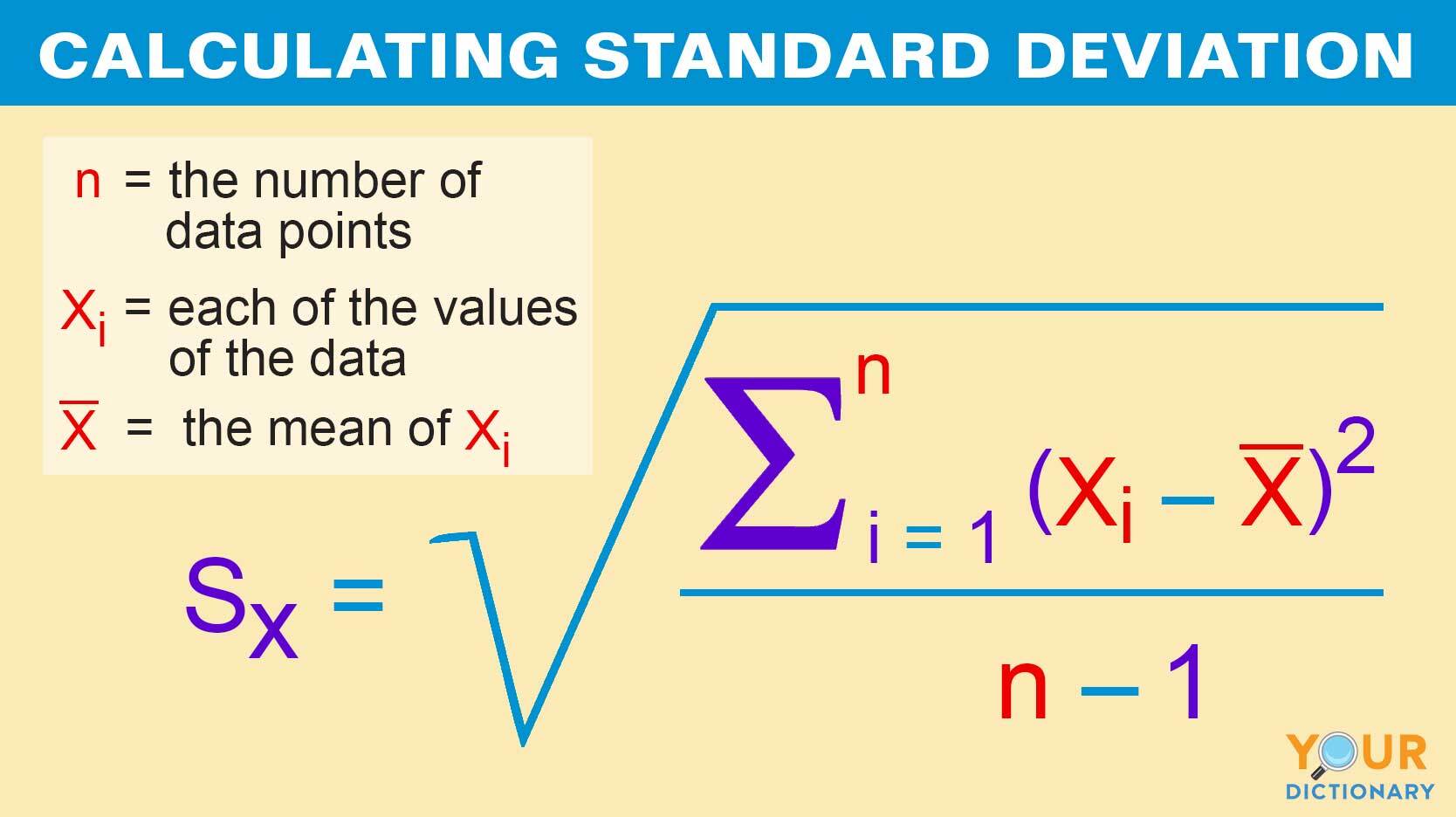
Standard Deviation Formula Np(1-P) . Σ = √ n*p*(1−p) where n is the sample size and p is the population proportion. The variance of the binomial distribution is σ 2 =npq, where n is the number of trials, p is the probability of success, and q i the probability of. X is the number of successes. A binomial distribution has the standard deviation $\sqrt{np(1−p)}$. The variance of a binomial distribution is given as: Let p = the probability the coin lands on heads. The larger the variance, the greater the fluctuation of a random variable from its mean. N is the number of trials. When you find the standard error of $\bar{x}$, you divide. To calculate the standard deviation for a given. For a binomial distribution, μ μ, the expected number of successes, σ2 σ 2, the variance, and σ σ, the standard deviation for the. P is the probability of a success.
from examples.yourdictionary.com
Let p = the probability the coin lands on heads. The variance of the binomial distribution is σ 2 =npq, where n is the number of trials, p is the probability of success, and q i the probability of. Σ = √ n*p*(1−p) where n is the sample size and p is the population proportion. P is the probability of a success. A binomial distribution has the standard deviation $\sqrt{np(1−p)}$. N is the number of trials. X is the number of successes. To calculate the standard deviation for a given. For a binomial distribution, μ μ, the expected number of successes, σ2 σ 2, the variance, and σ σ, the standard deviation for the. The variance of a binomial distribution is given as:
Examples of Standard Deviation and How It’s Used
Standard Deviation Formula Np(1-P) When you find the standard error of $\bar{x}$, you divide. P is the probability of a success. To calculate the standard deviation for a given. For a binomial distribution, μ μ, the expected number of successes, σ2 σ 2, the variance, and σ σ, the standard deviation for the. The variance of a binomial distribution is given as: N is the number of trials. A binomial distribution has the standard deviation $\sqrt{np(1−p)}$. When you find the standard error of $\bar{x}$, you divide. Σ = √ n*p*(1−p) where n is the sample size and p is the population proportion. Let p = the probability the coin lands on heads. The variance of the binomial distribution is σ 2 =npq, where n is the number of trials, p is the probability of success, and q i the probability of. X is the number of successes. The larger the variance, the greater the fluctuation of a random variable from its mean.
From cevxpnni.blob.core.windows.net
Calculate Standard Deviation In Statistics at Julie Cha blog Standard Deviation Formula Np(1-P) X is the number of successes. The larger the variance, the greater the fluctuation of a random variable from its mean. The variance of the binomial distribution is σ 2 =npq, where n is the number of trials, p is the probability of success, and q i the probability of. A binomial distribution has the standard deviation $\sqrt{np(1−p)}$. When you. Standard Deviation Formula Np(1-P).
From www.investopedia.com
Standard Deviation Formula and Uses vs. Variance Standard Deviation Formula Np(1-P) A binomial distribution has the standard deviation $\sqrt{np(1−p)}$. The variance of the binomial distribution is σ 2 =npq, where n is the number of trials, p is the probability of success, and q i the probability of. When you find the standard error of $\bar{x}$, you divide. The larger the variance, the greater the fluctuation of a random variable from. Standard Deviation Formula Np(1-P).
From www.youtube.com
Binomial Distribution Mean Variance Standard Deviation YouTube Standard Deviation Formula Np(1-P) To calculate the standard deviation for a given. X is the number of successes. For a binomial distribution, μ μ, the expected number of successes, σ2 σ 2, the variance, and σ σ, the standard deviation for the. Σ = √ n*p*(1−p) where n is the sample size and p is the population proportion. When you find the standard error. Standard Deviation Formula Np(1-P).
From examples.yourdictionary.com
Examples of Standard Deviation and How It’s Used Standard Deviation Formula Np(1-P) The larger the variance, the greater the fluctuation of a random variable from its mean. Σ = √ n*p*(1−p) where n is the sample size and p is the population proportion. When you find the standard error of $\bar{x}$, you divide. To calculate the standard deviation for a given. For a binomial distribution, μ μ, the expected number of successes,. Standard Deviation Formula Np(1-P).
From www.wikihow.com
How to Calculate Standard Deviation 12 Steps (with Pictures) Standard Deviation Formula Np(1-P) P is the probability of a success. To calculate the standard deviation for a given. The larger the variance, the greater the fluctuation of a random variable from its mean. The variance of the binomial distribution is σ 2 =npq, where n is the number of trials, p is the probability of success, and q i the probability of. For. Standard Deviation Formula Np(1-P).
From www.scribbr.co.uk
How to Calculate Standard Deviation (Guide) Calculator & Examples Standard Deviation Formula Np(1-P) The larger the variance, the greater the fluctuation of a random variable from its mean. To calculate the standard deviation for a given. Σ = √ n*p*(1−p) where n is the sample size and p is the population proportion. For a binomial distribution, μ μ, the expected number of successes, σ2 σ 2, the variance, and σ σ, the standard. Standard Deviation Formula Np(1-P).
From dxowvqajj.blob.core.windows.net
What Does Standard Deviation Mean Example at Nellie Koch blog Standard Deviation Formula Np(1-P) X is the number of successes. Σ = √ n*p*(1−p) where n is the sample size and p is the population proportion. N is the number of trials. When you find the standard error of $\bar{x}$, you divide. To calculate the standard deviation for a given. Let p = the probability the coin lands on heads. The variance of the. Standard Deviation Formula Np(1-P).
From www.slideserve.com
PPT Variance and Standard Deviation PowerPoint Presentation, free Standard Deviation Formula Np(1-P) To calculate the standard deviation for a given. The variance of a binomial distribution is given as: N is the number of trials. P is the probability of a success. X is the number of successes. The larger the variance, the greater the fluctuation of a random variable from its mean. Σ = √ n*p*(1−p) where n is the sample. Standard Deviation Formula Np(1-P).
From www.researchgate.net
Checking assumption, nP and n(1P) for calculated sample sizes Standard Deviation Formula Np(1-P) When you find the standard error of $\bar{x}$, you divide. The variance of the binomial distribution is σ 2 =npq, where n is the number of trials, p is the probability of success, and q i the probability of. N is the number of trials. P is the probability of a success. Let p = the probability the coin lands. Standard Deviation Formula Np(1-P).
From mungfali.com
Formula For Sample Standard Deviation Standard Deviation Formula Np(1-P) A binomial distribution has the standard deviation $\sqrt{np(1−p)}$. To calculate the standard deviation for a given. X is the number of successes. N is the number of trials. P is the probability of a success. Σ = √ n*p*(1−p) where n is the sample size and p is the population proportion. Let p = the probability the coin lands on. Standard Deviation Formula Np(1-P).
From discover.hubpages.com
How to Use Standard Deviation Formula For Equations (Statistics Help Standard Deviation Formula Np(1-P) To calculate the standard deviation for a given. The variance of the binomial distribution is σ 2 =npq, where n is the number of trials, p is the probability of success, and q i the probability of. When you find the standard error of $\bar{x}$, you divide. A binomial distribution has the standard deviation $\sqrt{np(1−p)}$. P is the probability of. Standard Deviation Formula Np(1-P).
From medium.com
Standard Deviation (Formula and Calculation Steps) ERP Information Standard Deviation Formula Np(1-P) P is the probability of a success. The larger the variance, the greater the fluctuation of a random variable from its mean. N is the number of trials. Let p = the probability the coin lands on heads. For a binomial distribution, μ μ, the expected number of successes, σ2 σ 2, the variance, and σ σ, the standard deviation. Standard Deviation Formula Np(1-P).
From curvebreakerstestprep.com
Standard Deviation Variation from the Mean Curvebreakers Standard Deviation Formula Np(1-P) A binomial distribution has the standard deviation $\sqrt{np(1−p)}$. For a binomial distribution, μ μ, the expected number of successes, σ2 σ 2, the variance, and σ σ, the standard deviation for the. Let p = the probability the coin lands on heads. The variance of the binomial distribution is σ 2 =npq, where n is the number of trials, p. Standard Deviation Formula Np(1-P).
From datascienceparichay.com
Calculate Standard Deviation in Python Data Science Parichay Standard Deviation Formula Np(1-P) When you find the standard error of $\bar{x}$, you divide. X is the number of successes. For a binomial distribution, μ μ, the expected number of successes, σ2 σ 2, the variance, and σ σ, the standard deviation for the. The variance of the binomial distribution is σ 2 =npq, where n is the number of trials, p is the. Standard Deviation Formula Np(1-P).
From www.cuemath.com
What Is Sample Standard Deviation Formula? Examples Standard Deviation Formula Np(1-P) Let p = the probability the coin lands on heads. Σ = √ n*p*(1−p) where n is the sample size and p is the population proportion. The variance of the binomial distribution is σ 2 =npq, where n is the number of trials, p is the probability of success, and q i the probability of. For a binomial distribution, μ. Standard Deviation Formula Np(1-P).
From www.youtube.com
How To Calculate The Standard Deviation Clearly Explained! YouTube Standard Deviation Formula Np(1-P) Σ = √ n*p*(1−p) where n is the sample size and p is the population proportion. N is the number of trials. P is the probability of a success. When you find the standard error of $\bar{x}$, you divide. X is the number of successes. To calculate the standard deviation for a given. The variance of a binomial distribution is. Standard Deviation Formula Np(1-P).
From haipernews.com
How To Calculate Standard Deviation Formula Haiper Standard Deviation Formula Np(1-P) N is the number of trials. The larger the variance, the greater the fluctuation of a random variable from its mean. Σ = √ n*p*(1−p) where n is the sample size and p is the population proportion. To calculate the standard deviation for a given. X is the number of successes. The variance of the binomial distribution is σ 2. Standard Deviation Formula Np(1-P).
From curvebreakerstestprep.com
Standard Deviation Variation from the Mean Curvebreakers Standard Deviation Formula Np(1-P) X is the number of successes. Σ = √ n*p*(1−p) where n is the sample size and p is the population proportion. For a binomial distribution, μ μ, the expected number of successes, σ2 σ 2, the variance, and σ σ, the standard deviation for the. N is the number of trials. Let p = the probability the coin lands. Standard Deviation Formula Np(1-P).
From articles.outlier.org
Sample Standard Deviation What is It & How to Calculate It Outlier Standard Deviation Formula Np(1-P) Let p = the probability the coin lands on heads. The variance of the binomial distribution is σ 2 =npq, where n is the number of trials, p is the probability of success, and q i the probability of. For a binomial distribution, μ μ, the expected number of successes, σ2 σ 2, the variance, and σ σ, the standard. Standard Deviation Formula Np(1-P).
From www.thoughtco.com
How to Calculate a Sample Standard Deviation Standard Deviation Formula Np(1-P) Let p = the probability the coin lands on heads. For a binomial distribution, μ μ, the expected number of successes, σ2 σ 2, the variance, and σ σ, the standard deviation for the. The variance of a binomial distribution is given as: To calculate the standard deviation for a given. P is the probability of a success. X is. Standard Deviation Formula Np(1-P).
From mungfali.com
Formula Of Standard Deviation Standard Deviation Formula Np(1-P) P is the probability of a success. Σ = √ n*p*(1−p) where n is the sample size and p is the population proportion. X is the number of successes. The variance of a binomial distribution is given as: The larger the variance, the greater the fluctuation of a random variable from its mean. When you find the standard error of. Standard Deviation Formula Np(1-P).
From cevxpnni.blob.core.windows.net
Calculate Standard Deviation In Statistics at Julie Cha blog Standard Deviation Formula Np(1-P) The larger the variance, the greater the fluctuation of a random variable from its mean. To calculate the standard deviation for a given. When you find the standard error of $\bar{x}$, you divide. For a binomial distribution, μ μ, the expected number of successes, σ2 σ 2, the variance, and σ σ, the standard deviation for the. Σ = √. Standard Deviation Formula Np(1-P).
From www.youtube.com
Standard Deviation divide by n or n1? YouTube Standard Deviation Formula Np(1-P) When you find the standard error of $\bar{x}$, you divide. N is the number of trials. For a binomial distribution, μ μ, the expected number of successes, σ2 σ 2, the variance, and σ σ, the standard deviation for the. The variance of the binomial distribution is σ 2 =npq, where n is the number of trials, p is the. Standard Deviation Formula Np(1-P).
From www.youtube.com
How to calculate Standard Deviation and Variance YouTube Standard Deviation Formula Np(1-P) N is the number of trials. A binomial distribution has the standard deviation $\sqrt{np(1−p)}$. The variance of the binomial distribution is σ 2 =npq, where n is the number of trials, p is the probability of success, and q i the probability of. Let p = the probability the coin lands on heads. To calculate the standard deviation for a. Standard Deviation Formula Np(1-P).
From www.teachoo.com
Example 10 Calculate mean, variance, standard deviation Standard Deviation Formula Np(1-P) For a binomial distribution, μ μ, the expected number of successes, σ2 σ 2, the variance, and σ σ, the standard deviation for the. To calculate the standard deviation for a given. The variance of the binomial distribution is σ 2 =npq, where n is the number of trials, p is the probability of success, and q i the probability. Standard Deviation Formula Np(1-P).
From www.chegg.com
Solved can you show how to get to the equation ( both the np Standard Deviation Formula Np(1-P) X is the number of successes. The variance of the binomial distribution is σ 2 =npq, where n is the number of trials, p is the probability of success, and q i the probability of. N is the number of trials. For a binomial distribution, μ μ, the expected number of successes, σ2 σ 2, the variance, and σ σ,. Standard Deviation Formula Np(1-P).
From slidetodoc.com
STANDARD DEVIATION Calculating and understanding standard deviation as Standard Deviation Formula Np(1-P) To calculate the standard deviation for a given. A binomial distribution has the standard deviation $\sqrt{np(1−p)}$. When you find the standard error of $\bar{x}$, you divide. The variance of a binomial distribution is given as: P is the probability of a success. Let p = the probability the coin lands on heads. The larger the variance, the greater the fluctuation. Standard Deviation Formula Np(1-P).
From www.youtube.com
How To Calculate The Standard Deviation YouTube Standard Deviation Formula Np(1-P) P is the probability of a success. Let p = the probability the coin lands on heads. A binomial distribution has the standard deviation $\sqrt{np(1−p)}$. Σ = √ n*p*(1−p) where n is the sample size and p is the population proportion. To calculate the standard deviation for a given. The larger the variance, the greater the fluctuation of a random. Standard Deviation Formula Np(1-P).
From qualityamerica.com
Np Chart Calculations Np Chart Formula Quality America Standard Deviation Formula Np(1-P) When you find the standard error of $\bar{x}$, you divide. N is the number of trials. The larger the variance, the greater the fluctuation of a random variable from its mean. Σ = √ n*p*(1−p) where n is the sample size and p is the population proportion. The variance of a binomial distribution is given as: The variance of the. Standard Deviation Formula Np(1-P).
From www.youtube.com
How to Calculate Standard Deviation by Hand YouTube Standard Deviation Formula Np(1-P) P is the probability of a success. N is the number of trials. The variance of the binomial distribution is σ 2 =npq, where n is the number of trials, p is the probability of success, and q i the probability of. When you find the standard error of $\bar{x}$, you divide. For a binomial distribution, μ μ, the expected. Standard Deviation Formula Np(1-P).
From dxoibzeta.blob.core.windows.net
Standard Deviation Definition Math Example at Angela Carr blog Standard Deviation Formula Np(1-P) X is the number of successes. Let p = the probability the coin lands on heads. N is the number of trials. For a binomial distribution, μ μ, the expected number of successes, σ2 σ 2, the variance, and σ σ, the standard deviation for the. When you find the standard error of $\bar{x}$, you divide. To calculate the standard. Standard Deviation Formula Np(1-P).
From www.sharpsightlabs.com
Numpy standard deviation explained Sharp Sight Standard Deviation Formula Np(1-P) Σ = √ n*p*(1−p) where n is the sample size and p is the population proportion. A binomial distribution has the standard deviation $\sqrt{np(1−p)}$. N is the number of trials. Let p = the probability the coin lands on heads. To calculate the standard deviation for a given. For a binomial distribution, μ μ, the expected number of successes, σ2. Standard Deviation Formula Np(1-P).
From blog.finxter.com
How to Calculate the Standard Deviation in NumPy? Be on the Right Standard Deviation Formula Np(1-P) N is the number of trials. Let p = the probability the coin lands on heads. Σ = √ n*p*(1−p) where n is the sample size and p is the population proportion. X is the number of successes. For a binomial distribution, μ μ, the expected number of successes, σ2 σ 2, the variance, and σ σ, the standard deviation. Standard Deviation Formula Np(1-P).
From www.kristakingmath.com
How to find Mean, variance, and standard deviation — Krista King Math Standard Deviation Formula Np(1-P) X is the number of successes. The variance of the binomial distribution is σ 2 =npq, where n is the number of trials, p is the probability of success, and q i the probability of. When you find the standard error of $\bar{x}$, you divide. The variance of a binomial distribution is given as: To calculate the standard deviation for. Standard Deviation Formula Np(1-P).
From www.erp-information.com
Standard Deviation (Formula, Example, and Calculation) Standard Deviation Formula Np(1-P) The larger the variance, the greater the fluctuation of a random variable from its mean. Σ = √ n*p*(1−p) where n is the sample size and p is the population proportion. The variance of the binomial distribution is σ 2 =npq, where n is the number of trials, p is the probability of success, and q i the probability of.. Standard Deviation Formula Np(1-P).