Logic Of Cross Product . — the cross product and its properties. in spite of these oddities, the cross product is extremely useful in physics. the cross product is defined as the unique vector b\times c\in \bbb r^3 such that a\cdot (b\times c) = \det (a,b,c),\quad \forall a\in\bbb r^3 this is an implicit. The definition may appear strange and lacking. Where →r is the position vector of the particle, relative to the point o. The dot product is a multiplication of two vectors that results. — this product, called the cross product, is only defined for vectors in \(\mathbb{r}^{3}\). The dot product represents the similarity between vectors as a single number: We will use it to define the angular momentum vector →l of a particle, relative to a point o, as follows: For example, we can say that north and east are. defining the cross product. →l = →r × →p = m→r × →v.
from studylib.net
The definition may appear strange and lacking. defining the cross product. the cross product is defined as the unique vector b\times c\in \bbb r^3 such that a\cdot (b\times c) = \det (a,b,c),\quad \forall a\in\bbb r^3 this is an implicit. — this product, called the cross product, is only defined for vectors in \(\mathbb{r}^{3}\). For example, we can say that north and east are. We will use it to define the angular momentum vector →l of a particle, relative to a point o, as follows: in spite of these oddities, the cross product is extremely useful in physics. →l = →r × →p = m→r × →v. Where →r is the position vector of the particle, relative to the point o. The dot product represents the similarity between vectors as a single number:
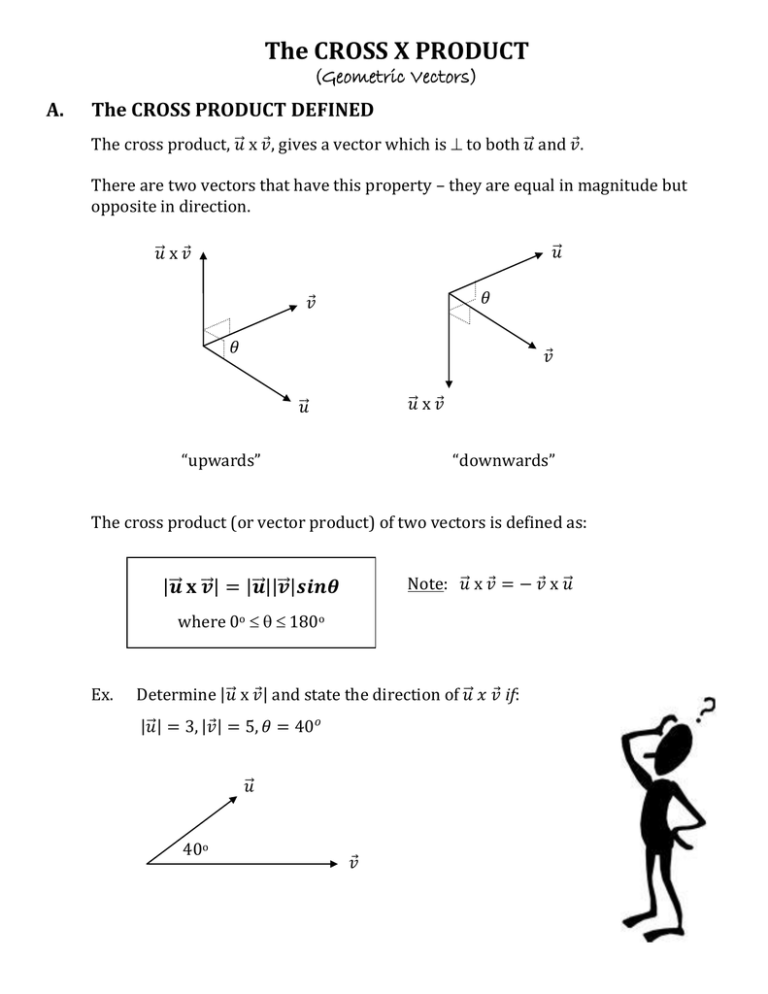
The CROSS X PRODUCT (Geometric Vectors) A. The CROSS PRODUCT DEFINED
Logic Of Cross Product For example, we can say that north and east are. defining the cross product. the cross product is defined as the unique vector b\times c\in \bbb r^3 such that a\cdot (b\times c) = \det (a,b,c),\quad \forall a\in\bbb r^3 this is an implicit. →l = →r × →p = m→r × →v. in spite of these oddities, the cross product is extremely useful in physics. The definition may appear strange and lacking. The dot product represents the similarity between vectors as a single number: The dot product is a multiplication of two vectors that results. — the cross product and its properties. We will use it to define the angular momentum vector →l of a particle, relative to a point o, as follows: For example, we can say that north and east are. Where →r is the position vector of the particle, relative to the point o. — this product, called the cross product, is only defined for vectors in \(\mathbb{r}^{3}\).
From www.slideserve.com
PPT Cross Product PowerPoint Presentation, free download ID9402769 Logic Of Cross Product We will use it to define the angular momentum vector →l of a particle, relative to a point o, as follows: →l = →r × →p = m→r × →v. the cross product is defined as the unique vector b\times c\in \bbb r^3 such that a\cdot (b\times c) = \det (a,b,c),\quad \forall a\in\bbb r^3 this is an implicit. . Logic Of Cross Product.
From www.showme.com
Cross Product and its Properties Math, Calculus, Cross products ShowMe Logic Of Cross Product For example, we can say that north and east are. We will use it to define the angular momentum vector →l of a particle, relative to a point o, as follows: — the cross product and its properties. Where →r is the position vector of the particle, relative to the point o. The definition may appear strange and lacking.. Logic Of Cross Product.
From www.youtube.com
Cross product of vectors Determinant method vs the direct calculation Logic Of Cross Product — the cross product and its properties. defining the cross product. For example, we can say that north and east are. — this product, called the cross product, is only defined for vectors in \(\mathbb{r}^{3}\). Where →r is the position vector of the particle, relative to the point o. the cross product is defined as the. Logic Of Cross Product.
From www.slideserve.com
PPT The Cross Product PowerPoint Presentation, free download ID3195487 Logic Of Cross Product the cross product is defined as the unique vector b\times c\in \bbb r^3 such that a\cdot (b\times c) = \det (a,b,c),\quad \forall a\in\bbb r^3 this is an implicit. Where →r is the position vector of the particle, relative to the point o. — this product, called the cross product, is only defined for vectors in \(\mathbb{r}^{3}\). —. Logic Of Cross Product.
From studylib.net
Lecture 3 Cross Products, Equations of Planes Logic Of Cross Product The definition may appear strange and lacking. The dot product represents the similarity between vectors as a single number: →l = →r × →p = m→r × →v. We will use it to define the angular momentum vector →l of a particle, relative to a point o, as follows: For example, we can say that north and east are. . Logic Of Cross Product.
From www.onenewspage.com
Properties of the Cross Product Vector Triple One News Page VIDEO Logic Of Cross Product The dot product is a multiplication of two vectors that results. in spite of these oddities, the cross product is extremely useful in physics. The definition may appear strange and lacking. the cross product is defined as the unique vector b\times c\in \bbb r^3 such that a\cdot (b\times c) = \det (a,b,c),\quad \forall a\in\bbb r^3 this is an. Logic Of Cross Product.
From www.slideserve.com
PPT The Cross Product of 2 Vectors 11.3 PowerPoint Presentation, free Logic Of Cross Product the cross product is defined as the unique vector b\times c\in \bbb r^3 such that a\cdot (b\times c) = \det (a,b,c),\quad \forall a\in\bbb r^3 this is an implicit. →l = →r × →p = m→r × →v. — this product, called the cross product, is only defined for vectors in \(\mathbb{r}^{3}\). Where →r is the position vector of. Logic Of Cross Product.
From en.neurochispas.com
Cross Product of Vectors Examples and Practice Neurochispas Logic Of Cross Product — the cross product and its properties. — this product, called the cross product, is only defined for vectors in \(\mathbb{r}^{3}\). The dot product is a multiplication of two vectors that results. For example, we can say that north and east are. in spite of these oddities, the cross product is extremely useful in physics. Where →r. Logic Of Cross Product.
From www.youtube.com
cross product exercise YouTube Logic Of Cross Product Where →r is the position vector of the particle, relative to the point o. the cross product is defined as the unique vector b\times c\in \bbb r^3 such that a\cdot (b\times c) = \det (a,b,c),\quad \forall a\in\bbb r^3 this is an implicit. — the cross product and its properties. defining the cross product. We will use it. Logic Of Cross Product.
From www.slideserve.com
PPT Cross Product PowerPoint Presentation, free download ID9402769 Logic Of Cross Product the cross product is defined as the unique vector b\times c\in \bbb r^3 such that a\cdot (b\times c) = \det (a,b,c),\quad \forall a\in\bbb r^3 this is an implicit. defining the cross product. — this product, called the cross product, is only defined for vectors in \(\mathbb{r}^{3}\). Where →r is the position vector of the particle, relative to. Logic Of Cross Product.
From www.youtube.com
Cross products in the light of linear transformations Chapter 11 Logic Of Cross Product the cross product is defined as the unique vector b\times c\in \bbb r^3 such that a\cdot (b\times c) = \det (a,b,c),\quad \forall a\in\bbb r^3 this is an implicit. →l = →r × →p = m→r × →v. in spite of these oddities, the cross product is extremely useful in physics. — the cross product and its properties.. Logic Of Cross Product.
From www.slideserve.com
PPT Cross Product PowerPoint Presentation, free download ID2849156 Logic Of Cross Product — the cross product and its properties. the cross product is defined as the unique vector b\times c\in \bbb r^3 such that a\cdot (b\times c) = \det (a,b,c),\quad \forall a\in\bbb r^3 this is an implicit. The dot product represents the similarity between vectors as a single number: The definition may appear strange and lacking. Where →r is the. Logic Of Cross Product.
From www.numerade.com
SOLVEDProve the specified property of cross products (Theorem 11 Logic Of Cross Product defining the cross product. We will use it to define the angular momentum vector →l of a particle, relative to a point o, as follows: in spite of these oddities, the cross product is extremely useful in physics. — the cross product and its properties. The definition may appear strange and lacking. →l = →r × →p. Logic Of Cross Product.
From studylib.net
The CROSS X PRODUCT (Geometric Vectors) A. The CROSS PRODUCT DEFINED Logic Of Cross Product in spite of these oddities, the cross product is extremely useful in physics. Where →r is the position vector of the particle, relative to the point o. — this product, called the cross product, is only defined for vectors in \(\mathbb{r}^{3}\). defining the cross product. The dot product represents the similarity between vectors as a single number:. Logic Of Cross Product.
From www.slideserve.com
PPT The Cross Product PowerPoint Presentation, free download ID3195487 Logic Of Cross Product We will use it to define the angular momentum vector →l of a particle, relative to a point o, as follows: The definition may appear strange and lacking. — this product, called the cross product, is only defined for vectors in \(\mathbb{r}^{3}\). →l = →r × →p = m→r × →v. in spite of these oddities, the cross. Logic Of Cross Product.
From www.pearson.com
Cross product, determinant method Pearson+ Channels Logic Of Cross Product the cross product is defined as the unique vector b\times c\in \bbb r^3 such that a\cdot (b\times c) = \det (a,b,c),\quad \forall a\in\bbb r^3 this is an implicit. defining the cross product. — this product, called the cross product, is only defined for vectors in \(\mathbb{r}^{3}\). The definition may appear strange and lacking. Where →r is the. Logic Of Cross Product.
From study.com
Cross Product Method Definition, Rules & Properties Lesson Logic Of Cross Product We will use it to define the angular momentum vector →l of a particle, relative to a point o, as follows: — the cross product and its properties. The dot product is a multiplication of two vectors that results. The dot product represents the similarity between vectors as a single number: the cross product is defined as the. Logic Of Cross Product.
From www.slideserve.com
PPT The Cross Product PowerPoint Presentation, free download ID3195487 Logic Of Cross Product the cross product is defined as the unique vector b\times c\in \bbb r^3 such that a\cdot (b\times c) = \det (a,b,c),\quad \forall a\in\bbb r^3 this is an implicit. — the cross product and its properties. The definition may appear strange and lacking. Where →r is the position vector of the particle, relative to the point o. in. Logic Of Cross Product.
From www.youtube.com
ProblemExpression of Cross Product in Terms of Components, Math Logic Of Cross Product Where →r is the position vector of the particle, relative to the point o. — the cross product and its properties. The dot product is a multiplication of two vectors that results. We will use it to define the angular momentum vector →l of a particle, relative to a point o, as follows: defining the cross product. . Logic Of Cross Product.
From calcworkshop.com
Cross Product for Calculus Everything You Need to Know Logic Of Cross Product the cross product is defined as the unique vector b\times c\in \bbb r^3 such that a\cdot (b\times c) = \det (a,b,c),\quad \forall a\in\bbb r^3 this is an implicit. For example, we can say that north and east are. The dot product is a multiplication of two vectors that results. We will use it to define the angular momentum vector. Logic Of Cross Product.
From www.youtube.com
The Cross Product Definition and Derivation YouTube Logic Of Cross Product — the cross product and its properties. The definition may appear strange and lacking. →l = →r × →p = m→r × →v. For example, we can say that north and east are. the cross product is defined as the unique vector b\times c\in \bbb r^3 such that a\cdot (b\times c) = \det (a,b,c),\quad \forall a\in\bbb r^3 this. Logic Of Cross Product.
From www.youtube.com
Properties of the Cross Product YouTube Logic Of Cross Product Where →r is the position vector of the particle, relative to the point o. We will use it to define the angular momentum vector →l of a particle, relative to a point o, as follows: in spite of these oddities, the cross product is extremely useful in physics. — this product, called the cross product, is only defined. Logic Of Cross Product.
From www.youtube.com
What is the CROSS PRODUCT and how to find the cross product of two Logic Of Cross Product — the cross product and its properties. The dot product represents the similarity between vectors as a single number: — this product, called the cross product, is only defined for vectors in \(\mathbb{r}^{3}\). defining the cross product. The dot product is a multiplication of two vectors that results. We will use it to define the angular momentum. Logic Of Cross Product.
From www.slideserve.com
PPT Consider the 2x2 matrix PowerPoint Presentation, free download Logic Of Cross Product in spite of these oddities, the cross product is extremely useful in physics. The dot product represents the similarity between vectors as a single number: the cross product is defined as the unique vector b\times c\in \bbb r^3 such that a\cdot (b\times c) = \det (a,b,c),\quad \forall a\in\bbb r^3 this is an implicit. We will use it to. Logic Of Cross Product.
From www.slideserve.com
PPT Cross Product PowerPoint Presentation, free download ID395792 Logic Of Cross Product For example, we can say that north and east are. Where →r is the position vector of the particle, relative to the point o. The definition may appear strange and lacking. — the cross product and its properties. defining the cross product. →l = →r × →p = m→r × →v. — this product, called the cross. Logic Of Cross Product.
From www.youtube.com
Introduction to the Cross Product, Part 2 of 3 Deriving the Formula Logic Of Cross Product We will use it to define the angular momentum vector →l of a particle, relative to a point o, as follows: The dot product is a multiplication of two vectors that results. For example, we can say that north and east are. in spite of these oddities, the cross product is extremely useful in physics. defining the cross. Logic Of Cross Product.
From socratic.org
What is the cross product of (4 i + 4 j + 2 k) and (5i + 12j + 2 k Logic Of Cross Product For example, we can say that north and east are. — the cross product and its properties. The definition may appear strange and lacking. We will use it to define the angular momentum vector →l of a particle, relative to a point o, as follows: in spite of these oddities, the cross product is extremely useful in physics.. Logic Of Cross Product.
From www.studocu.com
Explanation of how the cross product works Concordia University Logic Of Cross Product →l = →r × →p = m→r × →v. The dot product represents the similarity between vectors as a single number: — this product, called the cross product, is only defined for vectors in \(\mathbb{r}^{3}\). the cross product is defined as the unique vector b\times c\in \bbb r^3 such that a\cdot (b\times c) = \det (a,b,c),\quad \forall a\in\bbb. Logic Of Cross Product.
From www.cuemath.com
Cross Product Cuemath Logic Of Cross Product — the cross product and its properties. Where →r is the position vector of the particle, relative to the point o. The dot product is a multiplication of two vectors that results. in spite of these oddities, the cross product is extremely useful in physics. — this product, called the cross product, is only defined for vectors. Logic Of Cross Product.
From www.slideshare.net
Lesson 3 The Cross Product Logic Of Cross Product — this product, called the cross product, is only defined for vectors in \(\mathbb{r}^{3}\). defining the cross product. The dot product represents the similarity between vectors as a single number: The definition may appear strange and lacking. the cross product is defined as the unique vector b\times c\in \bbb r^3 such that a\cdot (b\times c) = \det. Logic Of Cross Product.
From www.youtube.com
How To Calculate Cross Product Matrix YouTube Logic Of Cross Product We will use it to define the angular momentum vector →l of a particle, relative to a point o, as follows: — the cross product and its properties. Where →r is the position vector of the particle, relative to the point o. →l = →r × →p = m→r × →v. The dot product represents the similarity between vectors. Logic Of Cross Product.
From www.slideserve.com
PPT Coordinate Systems PowerPoint Presentation, free download ID Logic Of Cross Product The dot product is a multiplication of two vectors that results. The definition may appear strange and lacking. — the cross product and its properties. →l = →r × →p = m→r × →v. For example, we can say that north and east are. — this product, called the cross product, is only defined for vectors in \(\mathbb{r}^{3}\).. Logic Of Cross Product.
From youtube.com
Very easy way to calculate the cross product Linear Algebra YouTube Logic Of Cross Product — this product, called the cross product, is only defined for vectors in \(\mathbb{r}^{3}\). We will use it to define the angular momentum vector →l of a particle, relative to a point o, as follows: — the cross product and its properties. The dot product is a multiplication of two vectors that results. the cross product is. Logic Of Cross Product.
From www.youtube.com
Cross Product of Two 3 by 3 Vectors (Linear Algebra) YouTube Logic Of Cross Product We will use it to define the angular momentum vector →l of a particle, relative to a point o, as follows: Where →r is the position vector of the particle, relative to the point o. →l = →r × →p = m→r × →v. The dot product is a multiplication of two vectors that results. the cross product is. Logic Of Cross Product.
From www.slideserve.com
PPT Cross Product PowerPoint Presentation, free download ID2849156 Logic Of Cross Product in spite of these oddities, the cross product is extremely useful in physics. The dot product represents the similarity between vectors as a single number: The dot product is a multiplication of two vectors that results. Where →r is the position vector of the particle, relative to the point o. The definition may appear strange and lacking. the. Logic Of Cross Product.