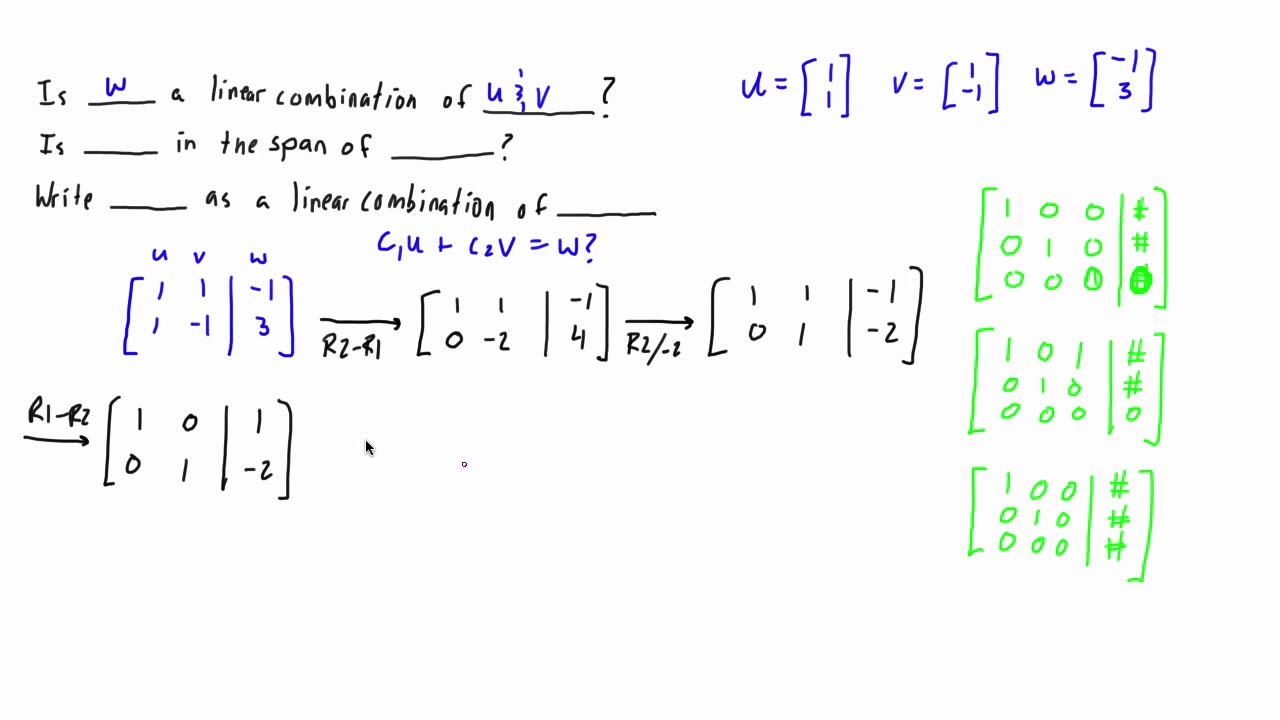Linear Combination Definition Finite . It is important to keep in mind that linear combinations are always finite, even if itds generating set is not. Set s s is infinitely linearly. Let \ (\vect {v}_1, \ldots, \vect {v}_n\) be vectors in \ (\mathbb {r}^m\). We could imagine a different definition: I understand that, for a vector space $v$ with scalar field $k$, the linear span of a family of vectors $s\subseteq v$ is usually. To illustrate this point, consider the vector space 𝕣[ x ] = span(1, x , x. If \(\mathbf{b}\) is in fact a linear combination of the two other vectors, then it can be written as \(x_1. Why do we restrict our attention to finite linear combinations? Any expression of the form \ [ x_1 \vect {v}_1+\cdots+x_n \vect {v}_n,\nonumber\] where \ (x_1,. We can use the definition of a linear combination to solve this problem. A subset of a vector space is linearly independent if none of its elements is a linear combination of the others.
from www.youtube.com
To illustrate this point, consider the vector space 𝕣[ x ] = span(1, x , x. Set s s is infinitely linearly. I understand that, for a vector space $v$ with scalar field $k$, the linear span of a family of vectors $s\subseteq v$ is usually. If \(\mathbf{b}\) is in fact a linear combination of the two other vectors, then it can be written as \(x_1. We could imagine a different definition: We can use the definition of a linear combination to solve this problem. It is important to keep in mind that linear combinations are always finite, even if itds generating set is not. Why do we restrict our attention to finite linear combinations? Any expression of the form \ [ x_1 \vect {v}_1+\cdots+x_n \vect {v}_n,\nonumber\] where \ (x_1,. Let \ (\vect {v}_1, \ldots, \vect {v}_n\) be vectors in \ (\mathbb {r}^m\).
How to determine if one vector is a linear combination of a set of
Linear Combination Definition Finite A subset of a vector space is linearly independent if none of its elements is a linear combination of the others. Let \ (\vect {v}_1, \ldots, \vect {v}_n\) be vectors in \ (\mathbb {r}^m\). To illustrate this point, consider the vector space 𝕣[ x ] = span(1, x , x. Set s s is infinitely linearly. We could imagine a different definition: I understand that, for a vector space $v$ with scalar field $k$, the linear span of a family of vectors $s\subseteq v$ is usually. It is important to keep in mind that linear combinations are always finite, even if itds generating set is not. A subset of a vector space is linearly independent if none of its elements is a linear combination of the others. Why do we restrict our attention to finite linear combinations? We can use the definition of a linear combination to solve this problem. Any expression of the form \ [ x_1 \vect {v}_1+\cdots+x_n \vect {v}_n,\nonumber\] where \ (x_1,. If \(\mathbf{b}\) is in fact a linear combination of the two other vectors, then it can be written as \(x_1.
From www.studypool.com
SOLUTION Lecture 18 linear combinations linear algebra Studypool Linear Combination Definition Finite We could imagine a different definition: Any expression of the form \ [ x_1 \vect {v}_1+\cdots+x_n \vect {v}_n,\nonumber\] where \ (x_1,. We can use the definition of a linear combination to solve this problem. Let \ (\vect {v}_1, \ldots, \vect {v}_n\) be vectors in \ (\mathbb {r}^m\). A subset of a vector space is linearly independent if none of its. Linear Combination Definition Finite.
From hxefydxia.blob.core.windows.net
Linear Combination Definition In Algebra at Timothy Lowery blog Linear Combination Definition Finite It is important to keep in mind that linear combinations are always finite, even if itds generating set is not. We could imagine a different definition: Any expression of the form \ [ x_1 \vect {v}_1+\cdots+x_n \vect {v}_n,\nonumber\] where \ (x_1,. We can use the definition of a linear combination to solve this problem. Let \ (\vect {v}_1, \ldots, \vect. Linear Combination Definition Finite.
From heung-bae-lee.github.io
Linear combination, vector equation, Four views of matrix Linear Combination Definition Finite Set s s is infinitely linearly. Why do we restrict our attention to finite linear combinations? To illustrate this point, consider the vector space 𝕣[ x ] = span(1, x , x. Let \ (\vect {v}_1, \ldots, \vect {v}_n\) be vectors in \ (\mathbb {r}^m\). We could imagine a different definition: If \(\mathbf{b}\) is in fact a linear combination of. Linear Combination Definition Finite.
From www.slideserve.com
PPT Lesson 58 Combinations PowerPoint Presentation, free download Linear Combination Definition Finite A subset of a vector space is linearly independent if none of its elements is a linear combination of the others. It is important to keep in mind that linear combinations are always finite, even if itds generating set is not. We could imagine a different definition: Set s s is infinitely linearly. Why do we restrict our attention to. Linear Combination Definition Finite.
From www.youtube.com
Linear Combination of vectors using i and j YouTube Linear Combination Definition Finite I understand that, for a vector space $v$ with scalar field $k$, the linear span of a family of vectors $s\subseteq v$ is usually. It is important to keep in mind that linear combinations are always finite, even if itds generating set is not. Set s s is infinitely linearly. If \(\mathbf{b}\) is in fact a linear combination of the. Linear Combination Definition Finite.
From www.youtube.com
Finite Element Method Example Complete Linear Analysis in Linear Combination Definition Finite We can use the definition of a linear combination to solve this problem. If \(\mathbf{b}\) is in fact a linear combination of the two other vectors, then it can be written as \(x_1. We could imagine a different definition: Why do we restrict our attention to finite linear combinations? Any expression of the form \ [ x_1 \vect {v}_1+\cdots+x_n \vect. Linear Combination Definition Finite.
From www.youtube.com
Linear AlgebraLinear CombinationDefinition and Examples YouTube Linear Combination Definition Finite To illustrate this point, consider the vector space 𝕣[ x ] = span(1, x , x. Why do we restrict our attention to finite linear combinations? Set s s is infinitely linearly. Let \ (\vect {v}_1, \ldots, \vect {v}_n\) be vectors in \ (\mathbb {r}^m\). We can use the definition of a linear combination to solve this problem. We could. Linear Combination Definition Finite.
From www.studocu.com
Linear Combinations and Spans Linear Combinations and Spans Linear Linear Combination Definition Finite To illustrate this point, consider the vector space 𝕣[ x ] = span(1, x , x. Let \ (\vect {v}_1, \ldots, \vect {v}_n\) be vectors in \ (\mathbb {r}^m\). Why do we restrict our attention to finite linear combinations? We can use the definition of a linear combination to solve this problem. It is important to keep in mind that. Linear Combination Definition Finite.
From ameiselive.com
Linear Algebra Linear Combination Worksheet Ameise Live Linear Combination Definition Finite I understand that, for a vector space $v$ with scalar field $k$, the linear span of a family of vectors $s\subseteq v$ is usually. A subset of a vector space is linearly independent if none of its elements is a linear combination of the others. Let \ (\vect {v}_1, \ldots, \vect {v}_n\) be vectors in \ (\mathbb {r}^m\). We can. Linear Combination Definition Finite.
From www.studocu.com
INTRODUCTION TO LINEAR ALGEBRA Linear Combination Definition 1 Given Linear Combination Definition Finite If \(\mathbf{b}\) is in fact a linear combination of the two other vectors, then it can be written as \(x_1. We can use the definition of a linear combination to solve this problem. Let \ (\vect {v}_1, \ldots, \vect {v}_n\) be vectors in \ (\mathbb {r}^m\). Set s s is infinitely linearly. I understand that, for a vector space $v$. Linear Combination Definition Finite.
From www.slideserve.com
PPT Linear Constantcoefficient Difference Equations PowerPoint Linear Combination Definition Finite Why do we restrict our attention to finite linear combinations? I understand that, for a vector space $v$ with scalar field $k$, the linear span of a family of vectors $s\subseteq v$ is usually. If \(\mathbf{b}\) is in fact a linear combination of the two other vectors, then it can be written as \(x_1. Any expression of the form \. Linear Combination Definition Finite.
From www.chegg.com
Solved The boundaryvalue problem y" = 4(yx), 0x1. Linear Combination Definition Finite Set s s is infinitely linearly. If \(\mathbf{b}\) is in fact a linear combination of the two other vectors, then it can be written as \(x_1. It is important to keep in mind that linear combinations are always finite, even if itds generating set is not. Let \ (\vect {v}_1, \ldots, \vect {v}_n\) be vectors in \ (\mathbb {r}^m\). To. Linear Combination Definition Finite.
From www.youtube.com
Definition of Linear Combination and How to Show a Vector is a Linear Linear Combination Definition Finite We can use the definition of a linear combination to solve this problem. To illustrate this point, consider the vector space 𝕣[ x ] = span(1, x , x. Let \ (\vect {v}_1, \ldots, \vect {v}_n\) be vectors in \ (\mathbb {r}^m\). We could imagine a different definition: I understand that, for a vector space $v$ with scalar field $k$,. Linear Combination Definition Finite.
From www.youtube.com
Linear Combination Definition Examples Revision Lecture 3 YouTube Linear Combination Definition Finite Any expression of the form \ [ x_1 \vect {v}_1+\cdots+x_n \vect {v}_n,\nonumber\] where \ (x_1,. Let \ (\vect {v}_1, \ldots, \vect {v}_n\) be vectors in \ (\mathbb {r}^m\). To illustrate this point, consider the vector space 𝕣[ x ] = span(1, x , x. We could imagine a different definition: I understand that, for a vector space $v$ with scalar. Linear Combination Definition Finite.
From www.youtube.com
Linear Combinations and Span YouTube Linear Combination Definition Finite Let \ (\vect {v}_1, \ldots, \vect {v}_n\) be vectors in \ (\mathbb {r}^m\). It is important to keep in mind that linear combinations are always finite, even if itds generating set is not. Any expression of the form \ [ x_1 \vect {v}_1+\cdots+x_n \vect {v}_n,\nonumber\] where \ (x_1,. If \(\mathbf{b}\) is in fact a linear combination of the two other. Linear Combination Definition Finite.
From www.youtube.com
Determine if b is a linear combination of vectors formed from the Linear Combination Definition Finite Any expression of the form \ [ x_1 \vect {v}_1+\cdots+x_n \vect {v}_n,\nonumber\] where \ (x_1,. Let \ (\vect {v}_1, \ldots, \vect {v}_n\) be vectors in \ (\mathbb {r}^m\). We can use the definition of a linear combination to solve this problem. Why do we restrict our attention to finite linear combinations? We could imagine a different definition: It is important. Linear Combination Definition Finite.
From studylib.net
Linear Transformation Linear Combination Definition Finite A subset of a vector space is linearly independent if none of its elements is a linear combination of the others. Set s s is infinitely linearly. Why do we restrict our attention to finite linear combinations? It is important to keep in mind that linear combinations are always finite, even if itds generating set is not. I understand that,. Linear Combination Definition Finite.
From www.studypool.com
SOLUTION Lecture 18 linear combinations linear algebra Studypool Linear Combination Definition Finite Why do we restrict our attention to finite linear combinations? Set s s is infinitely linearly. We can use the definition of a linear combination to solve this problem. Let \ (\vect {v}_1, \ldots, \vect {v}_n\) be vectors in \ (\mathbb {r}^m\). We could imagine a different definition: I understand that, for a vector space $v$ with scalar field $k$,. Linear Combination Definition Finite.
From www.slideserve.com
PPT Sampling Theory PowerPoint Presentation, free download ID9665820 Linear Combination Definition Finite We can use the definition of a linear combination to solve this problem. A subset of a vector space is linearly independent if none of its elements is a linear combination of the others. Let \ (\vect {v}_1, \ldots, \vect {v}_n\) be vectors in \ (\mathbb {r}^m\). It is important to keep in mind that linear combinations are always finite,. Linear Combination Definition Finite.
From www.chegg.com
Solved LINEAR COMBINATIONS OF VECTORS IN A VECTOR SPACE Linear Combination Definition Finite If \(\mathbf{b}\) is in fact a linear combination of the two other vectors, then it can be written as \(x_1. Let \ (\vect {v}_1, \ldots, \vect {v}_n\) be vectors in \ (\mathbb {r}^m\). I understand that, for a vector space $v$ with scalar field $k$, the linear span of a family of vectors $s\subseteq v$ is usually. Any expression of. Linear Combination Definition Finite.
From calcworkshop.com
Linear Combination of Random Variables (w/ 9 Examples!) Linear Combination Definition Finite It is important to keep in mind that linear combinations are always finite, even if itds generating set is not. We can use the definition of a linear combination to solve this problem. Set s s is infinitely linearly. A subset of a vector space is linearly independent if none of its elements is a linear combination of the others.. Linear Combination Definition Finite.
From www.youtube.com
Solving Systems Using Linear Combination (Simplifying Math) YouTube Linear Combination Definition Finite Set s s is infinitely linearly. We could imagine a different definition: I understand that, for a vector space $v$ with scalar field $k$, the linear span of a family of vectors $s\subseteq v$ is usually. If \(\mathbf{b}\) is in fact a linear combination of the two other vectors, then it can be written as \(x_1. We can use the. Linear Combination Definition Finite.
From www.youtube.com
Intro to Linear Combinations YouTube Linear Combination Definition Finite If \(\mathbf{b}\) is in fact a linear combination of the two other vectors, then it can be written as \(x_1. A subset of a vector space is linearly independent if none of its elements is a linear combination of the others. I understand that, for a vector space $v$ with scalar field $k$, the linear span of a family of. Linear Combination Definition Finite.
From www.youtube.com
Linear Algebra linear combination, matrix YouTube Linear Combination Definition Finite If \(\mathbf{b}\) is in fact a linear combination of the two other vectors, then it can be written as \(x_1. Set s s is infinitely linearly. Why do we restrict our attention to finite linear combinations? A subset of a vector space is linearly independent if none of its elements is a linear combination of the others. To illustrate this. Linear Combination Definition Finite.
From www.studocu.com
Depend 3. Linear Dependence and Span P. Danziger 1 Linear Combination Linear Combination Definition Finite Why do we restrict our attention to finite linear combinations? Set s s is infinitely linearly. I understand that, for a vector space $v$ with scalar field $k$, the linear span of a family of vectors $s\subseteq v$ is usually. We can use the definition of a linear combination to solve this problem. A subset of a vector space is. Linear Combination Definition Finite.
From www.slideserve.com
PPT Linear Constantcoefficient Difference Equations PowerPoint Linear Combination Definition Finite To illustrate this point, consider the vector space 𝕣[ x ] = span(1, x , x. Why do we restrict our attention to finite linear combinations? Let \ (\vect {v}_1, \ldots, \vect {v}_n\) be vectors in \ (\mathbb {r}^m\). We could imagine a different definition: We can use the definition of a linear combination to solve this problem. It is. Linear Combination Definition Finite.
From www.youtube.com
How to determine if one vector is a linear combination of a set of Linear Combination Definition Finite To illustrate this point, consider the vector space 𝕣[ x ] = span(1, x , x. A subset of a vector space is linearly independent if none of its elements is a linear combination of the others. Any expression of the form \ [ x_1 \vect {v}_1+\cdots+x_n \vect {v}_n,\nonumber\] where \ (x_1,. Set s s is infinitely linearly. We can. Linear Combination Definition Finite.
From www.slideserve.com
PPT ENGG2013 Unit 5 Linear Combination & Linear Independence Linear Combination Definition Finite Set s s is infinitely linearly. Let \ (\vect {v}_1, \ldots, \vect {v}_n\) be vectors in \ (\mathbb {r}^m\). It is important to keep in mind that linear combinations are always finite, even if itds generating set is not. To illustrate this point, consider the vector space 𝕣[ x ] = span(1, x , x. A subset of a vector. Linear Combination Definition Finite.
From www.slideserve.com
PPT Chapter 4 Chapter Content Real Vector Spaces Subspaces Linear Linear Combination Definition Finite Set s s is infinitely linearly. We can use the definition of a linear combination to solve this problem. To illustrate this point, consider the vector space 𝕣[ x ] = span(1, x , x. Why do we restrict our attention to finite linear combinations? We could imagine a different definition: I understand that, for a vector space $v$ with. Linear Combination Definition Finite.
From calcworkshop.com
Sigma Notation and Rules for Finite Sums (9 Surefire Examples) Linear Combination Definition Finite Set s s is infinitely linearly. Why do we restrict our attention to finite linear combinations? We could imagine a different definition: Any expression of the form \ [ x_1 \vect {v}_1+\cdots+x_n \vect {v}_n,\nonumber\] where \ (x_1,. It is important to keep in mind that linear combinations are always finite, even if itds generating set is not. I understand that,. Linear Combination Definition Finite.
From www.studocu.com
Linear Combinations and Span Linear Combinations and Span Definition Linear Combination Definition Finite If \(\mathbf{b}\) is in fact a linear combination of the two other vectors, then it can be written as \(x_1. We can use the definition of a linear combination to solve this problem. A subset of a vector space is linearly independent if none of its elements is a linear combination of the others. To illustrate this point, consider the. Linear Combination Definition Finite.
From www.youtube.com
Linear Combination YouTube Linear Combination Definition Finite It is important to keep in mind that linear combinations are always finite, even if itds generating set is not. A subset of a vector space is linearly independent if none of its elements is a linear combination of the others. We could imagine a different definition: If \(\mathbf{b}\) is in fact a linear combination of the two other vectors,. Linear Combination Definition Finite.
From datahacker.rs
Linear Algebra Linear combination of Vectors Master Data Science Linear Combination Definition Finite It is important to keep in mind that linear combinations are always finite, even if itds generating set is not. A subset of a vector space is linearly independent if none of its elements is a linear combination of the others. To illustrate this point, consider the vector space 𝕣[ x ] = span(1, x , x. Set s s. Linear Combination Definition Finite.
From people.eecs.ku.edu
Affine Transformations Linear Combination Definition Finite Let \ (\vect {v}_1, \ldots, \vect {v}_n\) be vectors in \ (\mathbb {r}^m\). We can use the definition of a linear combination to solve this problem. Why do we restrict our attention to finite linear combinations? We could imagine a different definition: To illustrate this point, consider the vector space 𝕣[ x ] = span(1, x , x. I understand. Linear Combination Definition Finite.
From faculty.washington.edu
Linear Finite Elements Linear Combination Definition Finite Why do we restrict our attention to finite linear combinations? It is important to keep in mind that linear combinations are always finite, even if itds generating set is not. Let \ (\vect {v}_1, \ldots, \vect {v}_n\) be vectors in \ (\mathbb {r}^m\). We could imagine a different definition: I understand that, for a vector space $v$ with scalar field. Linear Combination Definition Finite.