What Does Basis Vectors Mean In Linear Algebra . Any vector in the space can be expressed as a linear combination of these basis vectors. The two conditions such a set must satisfy in. In a vector space with basis the representation of with respect to is the column vector of the coefficients used to express as a. The basis theorem is an abstract version of the preceding statement, that applies to any subspace. In linear algebra, a basis vector refers to a vector that forms part of a basis for a vector space. A basis is a set of linearly. No vector can be represented as a linear combination of the other vectors. We know from the previous example 2.7.1 that r2 has dimension 2, so any basis of r2 has two vectors in it. A basis of a vector space is a set of vectors in that space that can be used as coordinates for it. Basis vectors in linear algebra, a set of vectors is considered a basis for a vector space if:
from medium.com
Basis vectors in linear algebra, a set of vectors is considered a basis for a vector space if: The basis theorem is an abstract version of the preceding statement, that applies to any subspace. Any vector in the space can be expressed as a linear combination of these basis vectors. A basis of a vector space is a set of vectors in that space that can be used as coordinates for it. In linear algebra, a basis vector refers to a vector that forms part of a basis for a vector space. In a vector space with basis the representation of with respect to is the column vector of the coefficients used to express as a. A basis is a set of linearly. The two conditions such a set must satisfy in. We know from the previous example 2.7.1 that r2 has dimension 2, so any basis of r2 has two vectors in it. No vector can be represented as a linear combination of the other vectors.
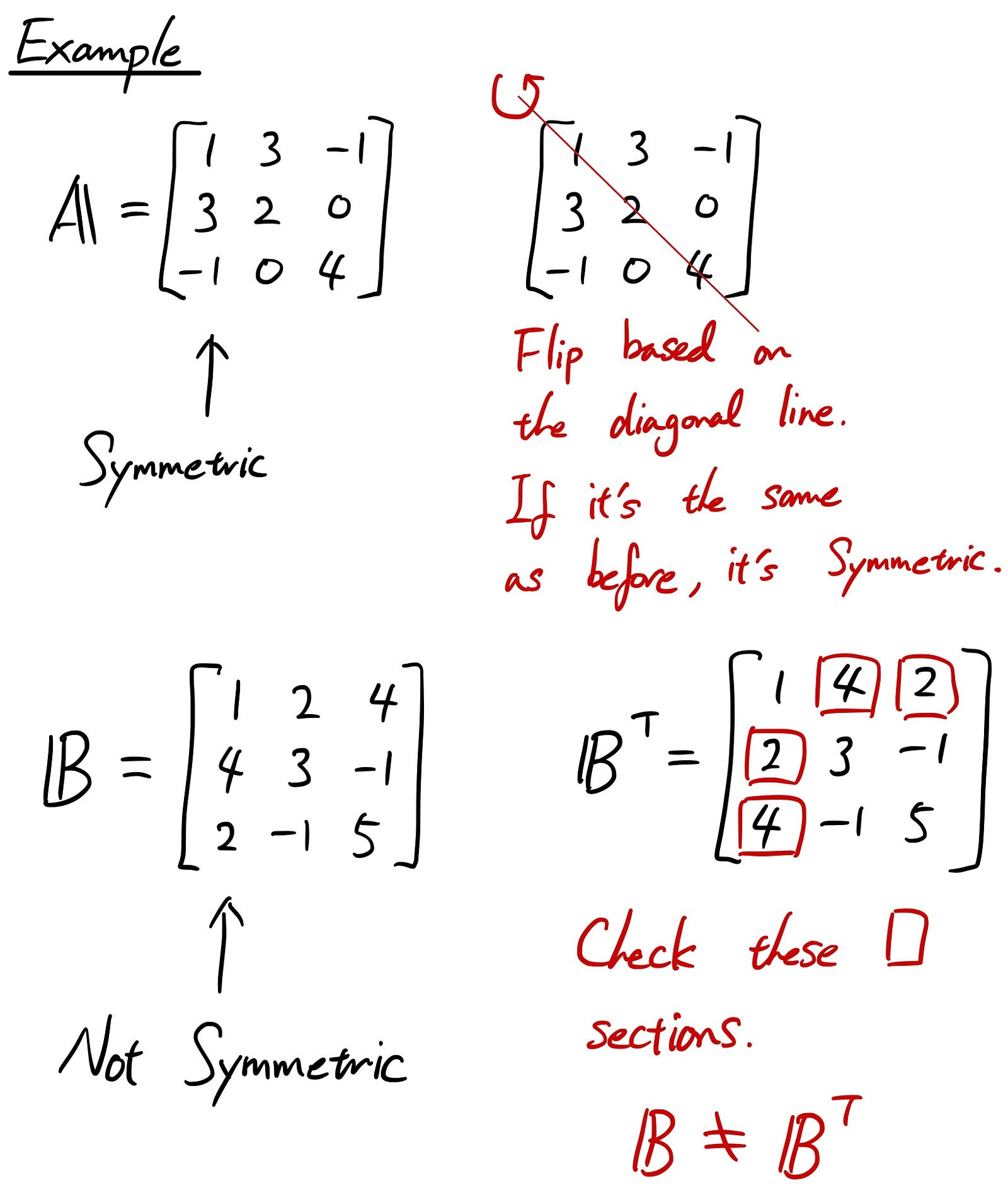
Linear Algebra 101 — Part 7 when symmetric
What Does Basis Vectors Mean In Linear Algebra A basis is a set of linearly. In a vector space with basis the representation of with respect to is the column vector of the coefficients used to express as a. A basis of a vector space is a set of vectors in that space that can be used as coordinates for it. A basis is a set of linearly. The basis theorem is an abstract version of the preceding statement, that applies to any subspace. No vector can be represented as a linear combination of the other vectors. Any vector in the space can be expressed as a linear combination of these basis vectors. The two conditions such a set must satisfy in. Basis vectors in linear algebra, a set of vectors is considered a basis for a vector space if: In linear algebra, a basis vector refers to a vector that forms part of a basis for a vector space. We know from the previous example 2.7.1 that r2 has dimension 2, so any basis of r2 has two vectors in it.
From www.youtube.com
Linear Algebra Finding a basis for a line in R^2 YouTube What Does Basis Vectors Mean In Linear Algebra In linear algebra, a basis vector refers to a vector that forms part of a basis for a vector space. Basis vectors in linear algebra, a set of vectors is considered a basis for a vector space if: A basis is a set of linearly. The two conditions such a set must satisfy in. We know from the previous example. What Does Basis Vectors Mean In Linear Algebra.
From www.math.ucdavis.edu
How to Use MATLAB to Find a Basis for col(A) Consisting of Column Vectors What Does Basis Vectors Mean In Linear Algebra We know from the previous example 2.7.1 that r2 has dimension 2, so any basis of r2 has two vectors in it. Any vector in the space can be expressed as a linear combination of these basis vectors. The two conditions such a set must satisfy in. In a vector space with basis the representation of with respect to is. What Does Basis Vectors Mean In Linear Algebra.
From www.youtube.com
Linear combinations, span, and basis vectors Chapter 2, Essence of What Does Basis Vectors Mean In Linear Algebra No vector can be represented as a linear combination of the other vectors. The basis theorem is an abstract version of the preceding statement, that applies to any subspace. A basis is a set of linearly. Basis vectors in linear algebra, a set of vectors is considered a basis for a vector space if: In a vector space with basis. What Does Basis Vectors Mean In Linear Algebra.
From calcworkshop.com
3D Vectors (Fully Explained w/ StepbyStep Examples!) What Does Basis Vectors Mean In Linear Algebra Basis vectors in linear algebra, a set of vectors is considered a basis for a vector space if: In a vector space with basis the representation of with respect to is the column vector of the coefficients used to express as a. We know from the previous example 2.7.1 that r2 has dimension 2, so any basis of r2 has. What Does Basis Vectors Mean In Linear Algebra.
From www.youtube.com
Linear Algebra Check if a set is a basis of R^3 YouTube What Does Basis Vectors Mean In Linear Algebra In linear algebra, a basis vector refers to a vector that forms part of a basis for a vector space. A basis of a vector space is a set of vectors in that space that can be used as coordinates for it. In a vector space with basis the representation of with respect to is the column vector of the. What Does Basis Vectors Mean In Linear Algebra.
From www.youtube.com
Linear Algebra 3 Vector Algebra YouTube What Does Basis Vectors Mean In Linear Algebra The two conditions such a set must satisfy in. The basis theorem is an abstract version of the preceding statement, that applies to any subspace. In a vector space with basis the representation of with respect to is the column vector of the coefficients used to express as a. We know from the previous example 2.7.1 that r2 has dimension. What Does Basis Vectors Mean In Linear Algebra.
From slidesharetrick.blogspot.com
Change Of Basis Linear Algebra slidesharetrick What Does Basis Vectors Mean In Linear Algebra We know from the previous example 2.7.1 that r2 has dimension 2, so any basis of r2 has two vectors in it. Basis vectors in linear algebra, a set of vectors is considered a basis for a vector space if: A basis is a set of linearly. The two conditions such a set must satisfy in. Any vector in the. What Does Basis Vectors Mean In Linear Algebra.
From www.youtube.com
Basis of a Vector Space Linear Algebra Sec. 4.5 Part 1 YouTube What Does Basis Vectors Mean In Linear Algebra We know from the previous example 2.7.1 that r2 has dimension 2, so any basis of r2 has two vectors in it. In a vector space with basis the representation of with respect to is the column vector of the coefficients used to express as a. A basis of a vector space is a set of vectors in that space. What Does Basis Vectors Mean In Linear Algebra.
From www.youtube.com
Standard Basis Vectors i, j, k YouTube What Does Basis Vectors Mean In Linear Algebra The basis theorem is an abstract version of the preceding statement, that applies to any subspace. A basis of a vector space is a set of vectors in that space that can be used as coordinates for it. In linear algebra, a basis vector refers to a vector that forms part of a basis for a vector space. A basis. What Does Basis Vectors Mean In Linear Algebra.
From codanics.com
Vectors in Linear Algebra A Comprehensive Guide Codanics What Does Basis Vectors Mean In Linear Algebra A basis is a set of linearly. The two conditions such a set must satisfy in. The basis theorem is an abstract version of the preceding statement, that applies to any subspace. A basis of a vector space is a set of vectors in that space that can be used as coordinates for it. No vector can be represented as. What Does Basis Vectors Mean In Linear Algebra.
From www.youtube.com
Linear Algebra Example Problems Vector Space Basis Example 2 YouTube What Does Basis Vectors Mean In Linear Algebra The two conditions such a set must satisfy in. The basis theorem is an abstract version of the preceding statement, that applies to any subspace. Any vector in the space can be expressed as a linear combination of these basis vectors. Basis vectors in linear algebra, a set of vectors is considered a basis for a vector space if: We. What Does Basis Vectors Mean In Linear Algebra.
From www.youtube.com
Orthogonal and Orthonormal Vectors Linear Algebra YouTube What Does Basis Vectors Mean In Linear Algebra In a vector space with basis the representation of with respect to is the column vector of the coefficients used to express as a. The basis theorem is an abstract version of the preceding statement, that applies to any subspace. No vector can be represented as a linear combination of the other vectors. We know from the previous example 2.7.1. What Does Basis Vectors Mean In Linear Algebra.
From datahacker.rs
007 Linear Algebra Change of basis Master Data Science What Does Basis Vectors Mean In Linear Algebra A basis is a set of linearly. No vector can be represented as a linear combination of the other vectors. Basis vectors in linear algebra, a set of vectors is considered a basis for a vector space if: In linear algebra, a basis vector refers to a vector that forms part of a basis for a vector space. In a. What Does Basis Vectors Mean In Linear Algebra.
From www.youtube.com
Linear Algebra Example Problems Linearly Independent Vectors 1 YouTube What Does Basis Vectors Mean In Linear Algebra Basis vectors in linear algebra, a set of vectors is considered a basis for a vector space if: No vector can be represented as a linear combination of the other vectors. A basis is a set of linearly. The two conditions such a set must satisfy in. In linear algebra, a basis vector refers to a vector that forms part. What Does Basis Vectors Mean In Linear Algebra.
From www.youtube.com
Find a basis for the span of a set of vectors (either a subspace or a What Does Basis Vectors Mean In Linear Algebra A basis of a vector space is a set of vectors in that space that can be used as coordinates for it. In linear algebra, a basis vector refers to a vector that forms part of a basis for a vector space. No vector can be represented as a linear combination of the other vectors. The two conditions such a. What Does Basis Vectors Mean In Linear Algebra.
From www.slideserve.com
PPT Numerical Linear Algebra PowerPoint Presentation, free download What Does Basis Vectors Mean In Linear Algebra The two conditions such a set must satisfy in. A basis of a vector space is a set of vectors in that space that can be used as coordinates for it. Basis vectors in linear algebra, a set of vectors is considered a basis for a vector space if: The basis theorem is an abstract version of the preceding statement,. What Does Basis Vectors Mean In Linear Algebra.
From www.chegg.com
Solved [Linear Algebra] 1. Let e1, e2 and e3 be the What Does Basis Vectors Mean In Linear Algebra The two conditions such a set must satisfy in. A basis of a vector space is a set of vectors in that space that can be used as coordinates for it. In a vector space with basis the representation of with respect to is the column vector of the coefficients used to express as a. We know from the previous. What Does Basis Vectors Mean In Linear Algebra.
From www2.seas.gwu.edu
Linear Algebra What Does Basis Vectors Mean In Linear Algebra In a vector space with basis the representation of with respect to is the column vector of the coefficients used to express as a. No vector can be represented as a linear combination of the other vectors. The basis theorem is an abstract version of the preceding statement, that applies to any subspace. We know from the previous example 2.7.1. What Does Basis Vectors Mean In Linear Algebra.
From www.youtube.com
Basis Examples for Vector Spaces R^3 and Pn (Linear Independence and What Does Basis Vectors Mean In Linear Algebra Any vector in the space can be expressed as a linear combination of these basis vectors. In a vector space with basis the representation of with respect to is the column vector of the coefficients used to express as a. Basis vectors in linear algebra, a set of vectors is considered a basis for a vector space if: No vector. What Does Basis Vectors Mean In Linear Algebra.
From www.youtube.com
Intro to Linear Algebra Basis for Column Space YouTube What Does Basis Vectors Mean In Linear Algebra The basis theorem is an abstract version of the preceding statement, that applies to any subspace. No vector can be represented as a linear combination of the other vectors. A basis is a set of linearly. We know from the previous example 2.7.1 that r2 has dimension 2, so any basis of r2 has two vectors in it. Basis vectors. What Does Basis Vectors Mean In Linear Algebra.
From math.stackexchange.com
linear algebra Why use Transpose notation in standart basis vectors What Does Basis Vectors Mean In Linear Algebra Any vector in the space can be expressed as a linear combination of these basis vectors. A basis is a set of linearly. Basis vectors in linear algebra, a set of vectors is considered a basis for a vector space if: No vector can be represented as a linear combination of the other vectors. The two conditions such a set. What Does Basis Vectors Mean In Linear Algebra.
From www.youtube.com
How to Easily Find the Basis of the Span of Vectors Linear Algebra What Does Basis Vectors Mean In Linear Algebra A basis is a set of linearly. No vector can be represented as a linear combination of the other vectors. The two conditions such a set must satisfy in. In a vector space with basis the representation of with respect to is the column vector of the coefficients used to express as a. In linear algebra, a basis vector refers. What Does Basis Vectors Mean In Linear Algebra.
From www.youtube.com
Linear Algebra Example Problems Spanning Vectors 1 YouTube What Does Basis Vectors Mean In Linear Algebra The basis theorem is an abstract version of the preceding statement, that applies to any subspace. No vector can be represented as a linear combination of the other vectors. In a vector space with basis the representation of with respect to is the column vector of the coefficients used to express as a. A basis of a vector space is. What Does Basis Vectors Mean In Linear Algebra.
From medium.com
Linear Algebra 101 — Part 7 when symmetric What Does Basis Vectors Mean In Linear Algebra Basis vectors in linear algebra, a set of vectors is considered a basis for a vector space if: A basis of a vector space is a set of vectors in that space that can be used as coordinates for it. In linear algebra, a basis vector refers to a vector that forms part of a basis for a vector space.. What Does Basis Vectors Mean In Linear Algebra.
From www.youtube.com
Linear Algebra Example Problems Matrix Null Space Basis and Dimension What Does Basis Vectors Mean In Linear Algebra A basis is a set of linearly. Basis vectors in linear algebra, a set of vectors is considered a basis for a vector space if: No vector can be represented as a linear combination of the other vectors. The two conditions such a set must satisfy in. The basis theorem is an abstract version of the preceding statement, that applies. What Does Basis Vectors Mean In Linear Algebra.
From www.3blue1brown.com
3Blue1Brown What Does Basis Vectors Mean In Linear Algebra The two conditions such a set must satisfy in. In a vector space with basis the representation of with respect to is the column vector of the coefficients used to express as a. A basis is a set of linearly. Any vector in the space can be expressed as a linear combination of these basis vectors. No vector can be. What Does Basis Vectors Mean In Linear Algebra.
From www.youtube.com
Linear Algebra finding a basis for the space spanned by given vectors What Does Basis Vectors Mean In Linear Algebra In linear algebra, a basis vector refers to a vector that forms part of a basis for a vector space. Basis vectors in linear algebra, a set of vectors is considered a basis for a vector space if: We know from the previous example 2.7.1 that r2 has dimension 2, so any basis of r2 has two vectors in it.. What Does Basis Vectors Mean In Linear Algebra.
From www.youtube.com
Linear Algebra Example Problems Linearly Independent Vectors 2 YouTube What Does Basis Vectors Mean In Linear Algebra A basis of a vector space is a set of vectors in that space that can be used as coordinates for it. The two conditions such a set must satisfy in. Basis vectors in linear algebra, a set of vectors is considered a basis for a vector space if: No vector can be represented as a linear combination of the. What Does Basis Vectors Mean In Linear Algebra.
From www.youtube.com
Linear Algebra 145, Basis and Dimension YouTube What Does Basis Vectors Mean In Linear Algebra Any vector in the space can be expressed as a linear combination of these basis vectors. The two conditions such a set must satisfy in. The basis theorem is an abstract version of the preceding statement, that applies to any subspace. A basis of a vector space is a set of vectors in that space that can be used as. What Does Basis Vectors Mean In Linear Algebra.
From vectorified.com
Basis Vector at Collection of Basis Vector free for What Does Basis Vectors Mean In Linear Algebra The basis theorem is an abstract version of the preceding statement, that applies to any subspace. A basis is a set of linearly. In a vector space with basis the representation of with respect to is the column vector of the coefficients used to express as a. In linear algebra, a basis vector refers to a vector that forms part. What Does Basis Vectors Mean In Linear Algebra.
From www.geeksforgeeks.org
Basis Vectors in Linear Algebra ML What Does Basis Vectors Mean In Linear Algebra Any vector in the space can be expressed as a linear combination of these basis vectors. Basis vectors in linear algebra, a set of vectors is considered a basis for a vector space if: A basis of a vector space is a set of vectors in that space that can be used as coordinates for it. The two conditions such. What Does Basis Vectors Mean In Linear Algebra.
From sciencethedata.com
Linear Algebra How to Transform a Vector in a Changed Basis Science What Does Basis Vectors Mean In Linear Algebra The two conditions such a set must satisfy in. In a vector space with basis the representation of with respect to is the column vector of the coefficients used to express as a. A basis of a vector space is a set of vectors in that space that can be used as coordinates for it. We know from the previous. What Does Basis Vectors Mean In Linear Algebra.
From www.youtube.com
GramSchmidt example with 3 basis vectors Linear Algebra Khan What Does Basis Vectors Mean In Linear Algebra The basis theorem is an abstract version of the preceding statement, that applies to any subspace. Any vector in the space can be expressed as a linear combination of these basis vectors. A basis of a vector space is a set of vectors in that space that can be used as coordinates for it. In linear algebra, a basis vector. What Does Basis Vectors Mean In Linear Algebra.
From www.youtube.com
Proving a Set of Vectors is a Basis Linear Algebra YouTube What Does Basis Vectors Mean In Linear Algebra A basis is a set of linearly. Any vector in the space can be expressed as a linear combination of these basis vectors. Basis vectors in linear algebra, a set of vectors is considered a basis for a vector space if: A basis of a vector space is a set of vectors in that space that can be used as. What Does Basis Vectors Mean In Linear Algebra.
From study.com
Basis of a Vector Space Definition & Examples Lesson What Does Basis Vectors Mean In Linear Algebra Any vector in the space can be expressed as a linear combination of these basis vectors. No vector can be represented as a linear combination of the other vectors. A basis of a vector space is a set of vectors in that space that can be used as coordinates for it. A basis is a set of linearly. In linear. What Does Basis Vectors Mean In Linear Algebra.