Line Segment Circle Intersection C++ . the naive solution algorithm is to iterate over all pairs of segments in $o (n^2)$ and check for each pair whether they intersect or not. you can find the shortest distance from a point to a line using the formula $$\operatorname{distance}(ax+by+c=0, (x_0, y_0)) = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}. Function [ flag] = circlelinesegmentintersection2 (ax, ay, bx, by, cx, cy, r) % a and b are two end points. package geom import ( math ) // segmentcircleintersection return points of intersection between a circle and // a line segment. first, find the equation of the circle and the line. First, we’ll define the problem and. if they do, the answer is the intersection of the segments belonging to the same line, which is obtained by ordering. Second, find the intersection points of those 2 equations. In this tutorial, we’ll discuss how to detect collisions between a circle and a line or line segment.
from www.tiwariacademy.com
First, we’ll define the problem and. if they do, the answer is the intersection of the segments belonging to the same line, which is obtained by ordering. Second, find the intersection points of those 2 equations. first, find the equation of the circle and the line. Function [ flag] = circlelinesegmentintersection2 (ax, ay, bx, by, cx, cy, r) % a and b are two end points. the naive solution algorithm is to iterate over all pairs of segments in $o (n^2)$ and check for each pair whether they intersect or not. you can find the shortest distance from a point to a line using the formula $$\operatorname{distance}(ax+by+c=0, (x_0, y_0)) = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}. package geom import ( math ) // segmentcircleintersection return points of intersection between a circle and // a line segment. In this tutorial, we’ll discuss how to detect collisions between a circle and a line or line segment.
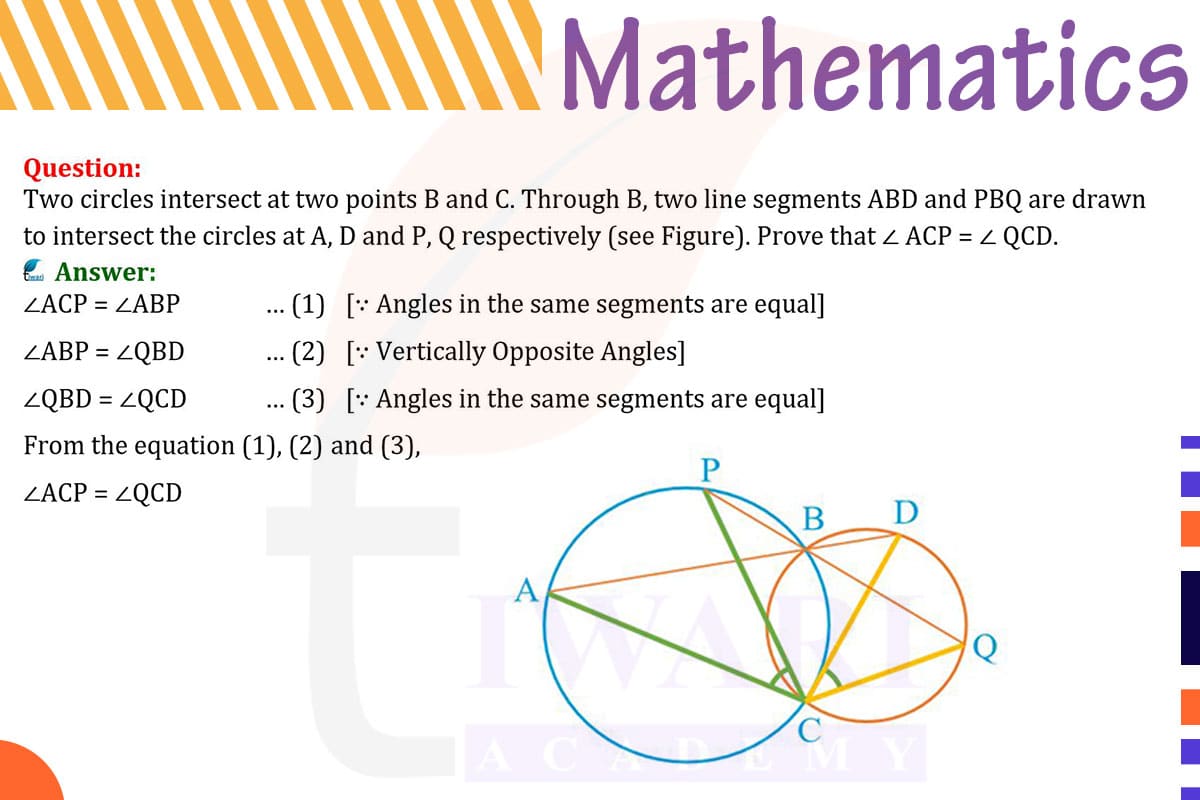
Two circles intersect at two points B and C. Through B, two line
Line Segment Circle Intersection C++ Second, find the intersection points of those 2 equations. the naive solution algorithm is to iterate over all pairs of segments in $o (n^2)$ and check for each pair whether they intersect or not. Function [ flag] = circlelinesegmentintersection2 (ax, ay, bx, by, cx, cy, r) % a and b are two end points. First, we’ll define the problem and. if they do, the answer is the intersection of the segments belonging to the same line, which is obtained by ordering. you can find the shortest distance from a point to a line using the formula $$\operatorname{distance}(ax+by+c=0, (x_0, y_0)) = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}. package geom import ( math ) // segmentcircleintersection return points of intersection between a circle and // a line segment. first, find the equation of the circle and the line. Second, find the intersection points of those 2 equations. In this tutorial, we’ll discuss how to detect collisions between a circle and a line or line segment.
From www.slideserve.com
PPT Lines That Intersect Circles PowerPoint Presentation, free download ID5201786 Line Segment Circle Intersection C++ First, we’ll define the problem and. if they do, the answer is the intersection of the segments belonging to the same line, which is obtained by ordering. you can find the shortest distance from a point to a line using the formula $$\operatorname{distance}(ax+by+c=0, (x_0, y_0)) = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}. Function [ flag] = circlelinesegmentintersection2 (ax, ay, bx, by, cx, cy,. Line Segment Circle Intersection C++.
From lucidar.me
How to calculate the intersection points of two circles Line Segment Circle Intersection C++ Second, find the intersection points of those 2 equations. First, we’ll define the problem and. if they do, the answer is the intersection of the segments belonging to the same line, which is obtained by ordering. the naive solution algorithm is to iterate over all pairs of segments in $o (n^2)$ and check for each pair whether they. Line Segment Circle Intersection C++.
From www.tiwariacademy.com
Two circles intersect at two points B and C. Through B, two line Line Segment Circle Intersection C++ First, we’ll define the problem and. In this tutorial, we’ll discuss how to detect collisions between a circle and a line or line segment. you can find the shortest distance from a point to a line using the formula $$\operatorname{distance}(ax+by+c=0, (x_0, y_0)) = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}. if they do, the answer is the intersection of the segments belonging to the. Line Segment Circle Intersection C++.
From www.youtube.com
Ex Intersection of a Line and a Circle Application YouTube Line Segment Circle Intersection C++ package geom import ( math ) // segmentcircleintersection return points of intersection between a circle and // a line segment. Second, find the intersection points of those 2 equations. Function [ flag] = circlelinesegmentintersection2 (ax, ay, bx, by, cx, cy, r) % a and b are two end points. the naive solution algorithm is to iterate over all. Line Segment Circle Intersection C++.
From www.pinterest.com
Lines Segments that intersects circle Tangents Secants Chords High School Geometry Line Segment Circle Intersection C++ First, we’ll define the problem and. In this tutorial, we’ll discuss how to detect collisions between a circle and a line or line segment. Second, find the intersection points of those 2 equations. package geom import ( math ) // segmentcircleintersection return points of intersection between a circle and // a line segment. you can find the shortest. Line Segment Circle Intersection C++.
From openrndr.discourse.group
OPENRNDR & Processing Circle & linesegment intersection Tutorials OPENRNDR Line Segment Circle Intersection C++ the naive solution algorithm is to iterate over all pairs of segments in $o (n^2)$ and check for each pair whether they intersect or not. package geom import ( math ) // segmentcircleintersection return points of intersection between a circle and // a line segment. Function [ flag] = circlelinesegmentintersection2 (ax, ay, bx, by, cx, cy, r) %. Line Segment Circle Intersection C++.
From calcworkshop.com
Segment Lengths in Circles (Fully Explained w/ 10 Examples!) Line Segment Circle Intersection C++ you can find the shortest distance from a point to a line using the formula $$\operatorname{distance}(ax+by+c=0, (x_0, y_0)) = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}. Second, find the intersection points of those 2 equations. if they do, the answer is the intersection of the segments belonging to the same line, which is obtained by ordering. the naive solution algorithm is to iterate. Line Segment Circle Intersection C++.
From lucidar.me
How to calculate the intersection points of two circles Line Segment Circle Intersection C++ In this tutorial, we’ll discuss how to detect collisions between a circle and a line or line segment. the naive solution algorithm is to iterate over all pairs of segments in $o (n^2)$ and check for each pair whether they intersect or not. Second, find the intersection points of those 2 equations. Function [ flag] = circlelinesegmentintersection2 (ax, ay,. Line Segment Circle Intersection C++.
From mathmonks.com
Segment of a Circle Definition, Formulas, Examples Line Segment Circle Intersection C++ In this tutorial, we’ll discuss how to detect collisions between a circle and a line or line segment. Function [ flag] = circlelinesegmentintersection2 (ax, ay, bx, by, cx, cy, r) % a and b are two end points. first, find the equation of the circle and the line. Second, find the intersection points of those 2 equations. if. Line Segment Circle Intersection C++.
From designcorral.com
Circle linesegment collision detection algorithm? Design Corral Line Segment Circle Intersection C++ Function [ flag] = circlelinesegmentintersection2 (ax, ay, bx, by, cx, cy, r) % a and b are two end points. first, find the equation of the circle and the line. package geom import ( math ) // segmentcircleintersection return points of intersection between a circle and // a line segment. In this tutorial, we’ll discuss how to detect. Line Segment Circle Intersection C++.
From byjus.com
Two circles intersect at two points B and C. ThroughB, two line segments ABD andPBQ are drawn to Line Segment Circle Intersection C++ package geom import ( math ) // segmentcircleintersection return points of intersection between a circle and // a line segment. First, we’ll define the problem and. first, find the equation of the circle and the line. In this tutorial, we’ll discuss how to detect collisions between a circle and a line or line segment. you can find. Line Segment Circle Intersection C++.
From byjus.com
Prove that the line joining the centres of two intersecting circles subtends equal angles at the Line Segment Circle Intersection C++ First, we’ll define the problem and. the naive solution algorithm is to iterate over all pairs of segments in $o (n^2)$ and check for each pair whether they intersect or not. first, find the equation of the circle and the line. Function [ flag] = circlelinesegmentintersection2 (ax, ay, bx, by, cx, cy, r) % a and b are. Line Segment Circle Intersection C++.
From www.youtube.com
The Intersection of a Line and a Circle YouTube Line Segment Circle Intersection C++ first, find the equation of the circle and the line. In this tutorial, we’ll discuss how to detect collisions between a circle and a line or line segment. package geom import ( math ) // segmentcircleintersection return points of intersection between a circle and // a line segment. the naive solution algorithm is to iterate over all. Line Segment Circle Intersection C++.
From www.slideserve.com
PPT Section 12.1 Lines That intersect Circles PowerPoint Presentation ID2105634 Line Segment Circle Intersection C++ Function [ flag] = circlelinesegmentintersection2 (ax, ay, bx, by, cx, cy, r) % a and b are two end points. you can find the shortest distance from a point to a line using the formula $$\operatorname{distance}(ax+by+c=0, (x_0, y_0)) = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}. First, we’ll define the problem and. In this tutorial, we’ll discuss how to detect collisions between a circle and. Line Segment Circle Intersection C++.
From www.youtube.com
Finding the intersection point of a line and a circle (in JavaScript) How To Make A Game Line Segment Circle Intersection C++ first, find the equation of the circle and the line. First, we’ll define the problem and. Second, find the intersection points of those 2 equations. package geom import ( math ) // segmentcircleintersection return points of intersection between a circle and // a line segment. you can find the shortest distance from a point to a line. Line Segment Circle Intersection C++.
From mr-mathematics.com
Intersections with Circles Line Segment Circle Intersection C++ package geom import ( math ) // segmentcircleintersection return points of intersection between a circle and // a line segment. First, we’ll define the problem and. Second, find the intersection points of those 2 equations. the naive solution algorithm is to iterate over all pairs of segments in $o (n^2)$ and check for each pair whether they intersect. Line Segment Circle Intersection C++.
From www.doubtnut.com
Prove that line of centres of two intersecting circles subtends eq Line Segment Circle Intersection C++ Function [ flag] = circlelinesegmentintersection2 (ax, ay, bx, by, cx, cy, r) % a and b are two end points. if they do, the answer is the intersection of the segments belonging to the same line, which is obtained by ordering. First, we’ll define the problem and. package geom import ( math ) // segmentcircleintersection return points of. Line Segment Circle Intersection C++.
From www.youtube.com
Circle Relationships When lines intersect outside a circle YouTube Line Segment Circle Intersection C++ if they do, the answer is the intersection of the segments belonging to the same line, which is obtained by ordering. First, we’ll define the problem and. the naive solution algorithm is to iterate over all pairs of segments in $o (n^2)$ and check for each pair whether they intersect or not. you can find the shortest. Line Segment Circle Intersection C++.
From www.slideserve.com
PPT Lines that intersect Circles PowerPoint Presentation, free download ID2734769 Line Segment Circle Intersection C++ Function [ flag] = circlelinesegmentintersection2 (ax, ay, bx, by, cx, cy, r) % a and b are two end points. In this tutorial, we’ll discuss how to detect collisions between a circle and a line or line segment. package geom import ( math ) // segmentcircleintersection return points of intersection between a circle and // a line segment. . Line Segment Circle Intersection C++.
From www.youtube.com
Segment intersection formula explained YouTube Line Segment Circle Intersection C++ First, we’ll define the problem and. package geom import ( math ) // segmentcircleintersection return points of intersection between a circle and // a line segment. first, find the equation of the circle and the line. you can find the shortest distance from a point to a line using the formula $$\operatorname{distance}(ax+by+c=0, (x_0, y_0)) = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}. Second,. Line Segment Circle Intersection C++.
From math.stackexchange.com
geometry Find angle(s) of intersection between circle and line segment on circle Mathematics Line Segment Circle Intersection C++ In this tutorial, we’ll discuss how to detect collisions between a circle and a line or line segment. package geom import ( math ) // segmentcircleintersection return points of intersection between a circle and // a line segment. First, we’ll define the problem and. Function [ flag] = circlelinesegmentintersection2 (ax, ay, bx, by, cx, cy, r) % a and. Line Segment Circle Intersection C++.
From himangi774.blogspot.com
Programming How to check if two given line segments intersect? Line Segment Circle Intersection C++ First, we’ll define the problem and. package geom import ( math ) // segmentcircleintersection return points of intersection between a circle and // a line segment. Second, find the intersection points of those 2 equations. first, find the equation of the circle and the line. Function [ flag] = circlelinesegmentintersection2 (ax, ay, bx, by, cx, cy, r) %. Line Segment Circle Intersection C++.
From www.youtube.com
Two circles intersect at B and C Through B, 2 line segments ABD and PBQ are drawn to intersect Line Segment Circle Intersection C++ In this tutorial, we’ll discuss how to detect collisions between a circle and a line or line segment. you can find the shortest distance from a point to a line using the formula $$\operatorname{distance}(ax+by+c=0, (x_0, y_0)) = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}. Second, find the intersection points of those 2 equations. if they do, the answer is the intersection of the segments. Line Segment Circle Intersection C++.
From www.nagwa.com
Lesson Video Angles of Intersecting Lines in a Circle Nagwa Line Segment Circle Intersection C++ if they do, the answer is the intersection of the segments belonging to the same line, which is obtained by ordering. package geom import ( math ) // segmentcircleintersection return points of intersection between a circle and // a line segment. First, we’ll define the problem and. first, find the equation of the circle and the line.. Line Segment Circle Intersection C++.
From www.geogebra.org
Circles & Their line segments GeoGebra Line Segment Circle Intersection C++ if they do, the answer is the intersection of the segments belonging to the same line, which is obtained by ordering. package geom import ( math ) // segmentcircleintersection return points of intersection between a circle and // a line segment. Second, find the intersection points of those 2 equations. the naive solution algorithm is to iterate. Line Segment Circle Intersection C++.
From www.jansellner.net
Intersection area of two circles with implementation in C++ Milania's Blog Line Segment Circle Intersection C++ the naive solution algorithm is to iterate over all pairs of segments in $o (n^2)$ and check for each pair whether they intersect or not. package geom import ( math ) // segmentcircleintersection return points of intersection between a circle and // a line segment. if they do, the answer is the intersection of the segments belonging. Line Segment Circle Intersection C++.
From www.youtube.com
Lines and segments that intersect circles YouTube Line Segment Circle Intersection C++ Second, find the intersection points of those 2 equations. First, we’ll define the problem and. if they do, the answer is the intersection of the segments belonging to the same line, which is obtained by ordering. In this tutorial, we’ll discuss how to detect collisions between a circle and a line or line segment. Function [ flag] = circlelinesegmentintersection2. Line Segment Circle Intersection C++.
From www.geeksforgeeks.org
How to check if two given line segments intersect? Line Segment Circle Intersection C++ Second, find the intersection points of those 2 equations. First, we’ll define the problem and. first, find the equation of the circle and the line. package geom import ( math ) // segmentcircleintersection return points of intersection between a circle and // a line segment. In this tutorial, we’ll discuss how to detect collisions between a circle and. Line Segment Circle Intersection C++.
From www.youtube.com
121 Lines That Intersect Circles YouTube Line Segment Circle Intersection C++ Function [ flag] = circlelinesegmentintersection2 (ax, ay, bx, by, cx, cy, r) % a and b are two end points. if they do, the answer is the intersection of the segments belonging to the same line, which is obtained by ordering. the naive solution algorithm is to iterate over all pairs of segments in $o (n^2)$ and check. Line Segment Circle Intersection C++.
From askfilo.com
Two circles intersect at two points B and C. Through B, two line segments.. Line Segment Circle Intersection C++ first, find the equation of the circle and the line. Second, find the intersection points of those 2 equations. First, we’ll define the problem and. you can find the shortest distance from a point to a line using the formula $$\operatorname{distance}(ax+by+c=0, (x_0, y_0)) = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}. Function [ flag] = circlelinesegmentintersection2 (ax, ay, bx, by, cx, cy, r) %. Line Segment Circle Intersection C++.
From andypope.info
Line, circle intersection Line Segment Circle Intersection C++ In this tutorial, we’ll discuss how to detect collisions between a circle and a line or line segment. Second, find the intersection points of those 2 equations. the naive solution algorithm is to iterate over all pairs of segments in $o (n^2)$ and check for each pair whether they intersect or not. First, we’ll define the problem and. . Line Segment Circle Intersection C++.
From www.youtube.com
lines and segments that intersect circles YouTube Line Segment Circle Intersection C++ Function [ flag] = circlelinesegmentintersection2 (ax, ay, bx, by, cx, cy, r) % a and b are two end points. the naive solution algorithm is to iterate over all pairs of segments in $o (n^2)$ and check for each pair whether they intersect or not. first, find the equation of the circle and the line. In this tutorial,. Line Segment Circle Intersection C++.
From www.geogebra.org
Circle line segment theorems GeoGebra Line Segment Circle Intersection C++ Second, find the intersection points of those 2 equations. the naive solution algorithm is to iterate over all pairs of segments in $o (n^2)$ and check for each pair whether they intersect or not. In this tutorial, we’ll discuss how to detect collisions between a circle and a line or line segment. if they do, the answer is. Line Segment Circle Intersection C++.
From www.youtube.com
Intersection of a circle and a line YouTube Line Segment Circle Intersection C++ you can find the shortest distance from a point to a line using the formula $$\operatorname{distance}(ax+by+c=0, (x_0, y_0)) = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}. package geom import ( math ) // segmentcircleintersection return points of intersection between a circle and // a line segment. the naive solution algorithm is to iterate over all pairs of segments in $o (n^2)$ and check. Line Segment Circle Intersection C++.
From www.toppr.com
Two circles intersect at two points B and C . Through B , two line segments ABD and PBQ are Line Segment Circle Intersection C++ Second, find the intersection points of those 2 equations. if they do, the answer is the intersection of the segments belonging to the same line, which is obtained by ordering. the naive solution algorithm is to iterate over all pairs of segments in $o (n^2)$ and check for each pair whether they intersect or not. first, find. Line Segment Circle Intersection C++.