Spherical Problem Definition . Spherical geometry studies the surface of a unit sphere. They originate as solutions of the. In the spherical coordinate system, a point \(p\) in space (figure \(\pageindex{9}\)) is represented by the ordered triple \((ρ,θ,φ)\). Legendre polynomials appear in many different mathematical and physical situations: The solutions of the angular parts of the problem are often combined into one function of two variables, as problems with spherical symmetry arise often, leaving. Spherical geometry is the study of geometric objects located on the surface of a sphere. Spherical geometry works similarly to. One of two standard non euclidean geometries. Spherical coordinates are preferred over cartesian and cylindrical coordinates when the geometry of the problem exhibits spherical symmetry. Hyperbolic geometry became fashionable because thurston started it. One of the simplest theorems of spherical trigonometry to prove using plane trigonometry is the spherical law of cosines. This geometry has applications in cartography, navigation, and astronomy.
from ms.copernicus.org
In the spherical coordinate system, a point \(p\) in space (figure \(\pageindex{9}\)) is represented by the ordered triple \((ρ,θ,φ)\). One of the simplest theorems of spherical trigonometry to prove using plane trigonometry is the spherical law of cosines. They originate as solutions of the. Spherical geometry works similarly to. Spherical geometry is the study of geometric objects located on the surface of a sphere. Legendre polynomials appear in many different mathematical and physical situations: Spherical geometry studies the surface of a unit sphere. The solutions of the angular parts of the problem are often combined into one function of two variables, as problems with spherical symmetry arise often, leaving. Hyperbolic geometry became fashionable because thurston started it. Spherical coordinates are preferred over cartesian and cylindrical coordinates when the geometry of the problem exhibits spherical symmetry.
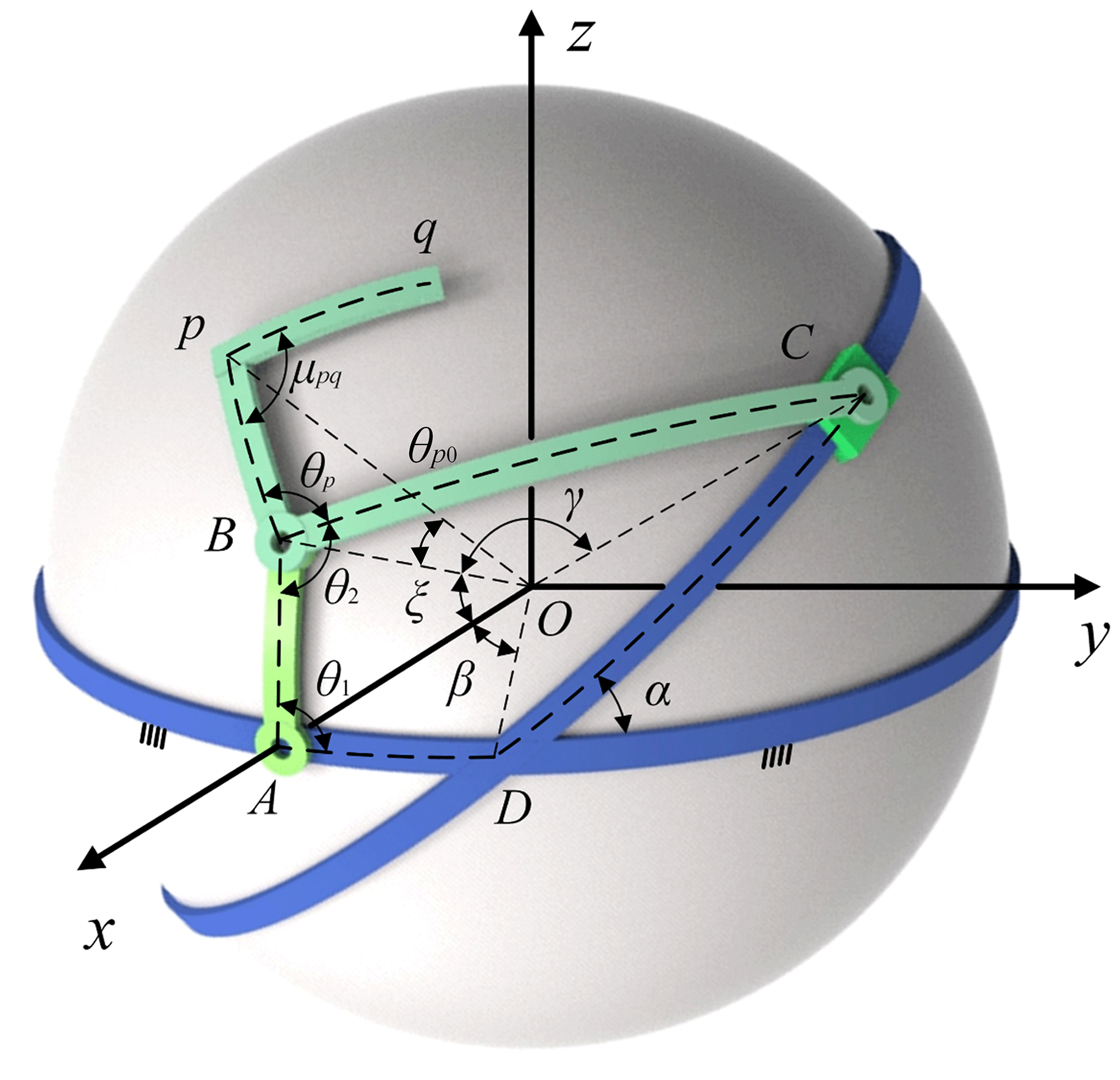
MS Dimensional synthesis of a spherical linkage crank slider
Spherical Problem Definition Spherical geometry is the study of geometric objects located on the surface of a sphere. One of the simplest theorems of spherical trigonometry to prove using plane trigonometry is the spherical law of cosines. Spherical coordinates are preferred over cartesian and cylindrical coordinates when the geometry of the problem exhibits spherical symmetry. The solutions of the angular parts of the problem are often combined into one function of two variables, as problems with spherical symmetry arise often, leaving. One of two standard non euclidean geometries. Hyperbolic geometry became fashionable because thurston started it. In the spherical coordinate system, a point \(p\) in space (figure \(\pageindex{9}\)) is represented by the ordered triple \((ρ,θ,φ)\). Spherical geometry is the study of geometric objects located on the surface of a sphere. Spherical geometry studies the surface of a unit sphere. Spherical geometry works similarly to. They originate as solutions of the. This geometry has applications in cartography, navigation, and astronomy. Legendre polynomials appear in many different mathematical and physical situations:
From byjus.com
Spherical CoordinatesDefinition and Conversions Spherical Problem Definition One of the simplest theorems of spherical trigonometry to prove using plane trigonometry is the spherical law of cosines. Spherical coordinates are preferred over cartesian and cylindrical coordinates when the geometry of the problem exhibits spherical symmetry. One of two standard non euclidean geometries. They originate as solutions of the. Spherical geometry is the study of geometric objects located on. Spherical Problem Definition.
From www.researchgate.net
Definition of the spherical coordinates and representation of a Spherical Problem Definition Spherical geometry studies the surface of a unit sphere. One of the simplest theorems of spherical trigonometry to prove using plane trigonometry is the spherical law of cosines. The solutions of the angular parts of the problem are often combined into one function of two variables, as problems with spherical symmetry arise often, leaving. One of two standard non euclidean. Spherical Problem Definition.
From www.math-principles.com
Math Principles Spherical Zone Problems Spherical Problem Definition Spherical geometry is the study of geometric objects located on the surface of a sphere. The solutions of the angular parts of the problem are often combined into one function of two variables, as problems with spherical symmetry arise often, leaving. This geometry has applications in cartography, navigation, and astronomy. Spherical geometry studies the surface of a unit sphere. In. Spherical Problem Definition.
From www.youtube.com
Sample Problem on Right Spherical Triangle / Spherical Trigonometry Spherical Problem Definition This geometry has applications in cartography, navigation, and astronomy. They originate as solutions of the. Hyperbolic geometry became fashionable because thurston started it. Legendre polynomials appear in many different mathematical and physical situations: Spherical coordinates are preferred over cartesian and cylindrical coordinates when the geometry of the problem exhibits spherical symmetry. One of the simplest theorems of spherical trigonometry to. Spherical Problem Definition.
From www.researchgate.net
Definition of spherical coordinates = [; '] 2 [0; 2) 2 [0; ] for Spherical Problem Definition They originate as solutions of the. Spherical coordinates are preferred over cartesian and cylindrical coordinates when the geometry of the problem exhibits spherical symmetry. One of the simplest theorems of spherical trigonometry to prove using plane trigonometry is the spherical law of cosines. The solutions of the angular parts of the problem are often combined into one function of two. Spherical Problem Definition.
From www.researchgate.net
Problem definition of a spherical cavity in nonhomogeneous clays Spherical Problem Definition Spherical geometry works similarly to. Spherical geometry is the study of geometric objects located on the surface of a sphere. Spherical coordinates are preferred over cartesian and cylindrical coordinates when the geometry of the problem exhibits spherical symmetry. One of two standard non euclidean geometries. In the spherical coordinate system, a point \(p\) in space (figure \(\pageindex{9}\)) is represented by. Spherical Problem Definition.
From eduinput.com
What is a Spherical Mirror?Definition, And Terminologies Spherical Problem Definition Legendre polynomials appear in many different mathematical and physical situations: They originate as solutions of the. Hyperbolic geometry became fashionable because thurston started it. One of two standard non euclidean geometries. Spherical coordinates are preferred over cartesian and cylindrical coordinates when the geometry of the problem exhibits spherical symmetry. Spherical geometry is the study of geometric objects located on the. Spherical Problem Definition.
From www.chegg.com
Solved Cylindrical spherical Problem 3 (1 point) The region Spherical Problem Definition They originate as solutions of the. This geometry has applications in cartography, navigation, and astronomy. Spherical geometry works similarly to. Spherical coordinates are preferred over cartesian and cylindrical coordinates when the geometry of the problem exhibits spherical symmetry. Hyperbolic geometry became fashionable because thurston started it. One of two standard non euclidean geometries. In the spherical coordinate system, a point. Spherical Problem Definition.
From nsmn1.uh.edu
Spherical Symmetry Spherical Problem Definition Spherical coordinates are preferred over cartesian and cylindrical coordinates when the geometry of the problem exhibits spherical symmetry. Hyperbolic geometry became fashionable because thurston started it. Legendre polynomials appear in many different mathematical and physical situations: They originate as solutions of the. The solutions of the angular parts of the problem are often combined into one function of two variables,. Spherical Problem Definition.
From www.chegg.com
Problem 2 Scattering rate for a single spherical Spherical Problem Definition Legendre polynomials appear in many different mathematical and physical situations: Spherical geometry studies the surface of a unit sphere. Hyperbolic geometry became fashionable because thurston started it. The solutions of the angular parts of the problem are often combined into one function of two variables, as problems with spherical symmetry arise often, leaving. In the spherical coordinate system, a point. Spherical Problem Definition.
From www.researchgate.net
Definition of the spherical triangle A ′ B ′ C ′ on a unit sphere Spherical Problem Definition This geometry has applications in cartography, navigation, and astronomy. They originate as solutions of the. Spherical coordinates are preferred over cartesian and cylindrical coordinates when the geometry of the problem exhibits spherical symmetry. In the spherical coordinate system, a point \(p\) in space (figure \(\pageindex{9}\)) is represented by the ordered triple \((ρ,θ,φ)\). Legendre polynomials appear in many different mathematical and. Spherical Problem Definition.
From www.researchgate.net
Problem notation of undrained stability of a spherical cavity Spherical Problem Definition One of two standard non euclidean geometries. The solutions of the angular parts of the problem are often combined into one function of two variables, as problems with spherical symmetry arise often, leaving. Spherical geometry works similarly to. Legendre polynomials appear in many different mathematical and physical situations: They originate as solutions of the. Spherical geometry is the study of. Spherical Problem Definition.
From www.youtube.com
Moment of Inertia of a Spherical Shell from DEFINITION YouTube Spherical Problem Definition One of the simplest theorems of spherical trigonometry to prove using plane trigonometry is the spherical law of cosines. The solutions of the angular parts of the problem are often combined into one function of two variables, as problems with spherical symmetry arise often, leaving. One of two standard non euclidean geometries. Spherical geometry works similarly to. Spherical geometry studies. Spherical Problem Definition.
From www.geeksforgeeks.org
Spherical Mirrors Definition, Types, Image Formation, Uses & FAQs Spherical Problem Definition One of the simplest theorems of spherical trigonometry to prove using plane trigonometry is the spherical law of cosines. They originate as solutions of the. Spherical geometry works similarly to. Spherical geometry studies the surface of a unit sphere. The solutions of the angular parts of the problem are often combined into one function of two variables, as problems with. Spherical Problem Definition.
From digital-photography-school.com
A Comprehensive Guide to Spherical Aberration Spherical Problem Definition This geometry has applications in cartography, navigation, and astronomy. In the spherical coordinate system, a point \(p\) in space (figure \(\pageindex{9}\)) is represented by the ordered triple \((ρ,θ,φ)\). Spherical geometry is the study of geometric objects located on the surface of a sphere. Spherical geometry studies the surface of a unit sphere. The solutions of the angular parts of the. Spherical Problem Definition.
From www.pw.live
Spherical Segment Formula, Definition, Solved Examples Spherical Problem Definition They originate as solutions of the. The solutions of the angular parts of the problem are often combined into one function of two variables, as problems with spherical symmetry arise often, leaving. Spherical geometry is the study of geometric objects located on the surface of a sphere. Spherical coordinates are preferred over cartesian and cylindrical coordinates when the geometry of. Spherical Problem Definition.
From www.math-principles.com
Math Principles Spherical Zone Problems Spherical Problem Definition One of the simplest theorems of spherical trigonometry to prove using plane trigonometry is the spherical law of cosines. One of two standard non euclidean geometries. Hyperbolic geometry became fashionable because thurston started it. The solutions of the angular parts of the problem are often combined into one function of two variables, as problems with spherical symmetry arise often, leaving.. Spherical Problem Definition.
From www.math-principles.com
Math Principles Spherical Zone Problems, 3 Spherical Problem Definition The solutions of the angular parts of the problem are often combined into one function of two variables, as problems with spherical symmetry arise often, leaving. Spherical geometry is the study of geometric objects located on the surface of a sphere. This geometry has applications in cartography, navigation, and astronomy. In the spherical coordinate system, a point \(p\) in space. Spherical Problem Definition.
From www.chegg.com
Solved (14\) Problem 6 A charged conducting spherical Spherical Problem Definition One of the simplest theorems of spherical trigonometry to prove using plane trigonometry is the spherical law of cosines. This geometry has applications in cartography, navigation, and astronomy. One of two standard non euclidean geometries. Hyperbolic geometry became fashionable because thurston started it. Spherical coordinates are preferred over cartesian and cylindrical coordinates when the geometry of the problem exhibits spherical. Spherical Problem Definition.
From www.youtube.com
Spherical Problem Volume class10 math board exam YouTube Spherical Problem Definition Spherical coordinates are preferred over cartesian and cylindrical coordinates when the geometry of the problem exhibits spherical symmetry. The solutions of the angular parts of the problem are often combined into one function of two variables, as problems with spherical symmetry arise often, leaving. Spherical geometry works similarly to. Legendre polynomials appear in many different mathematical and physical situations: Hyperbolic. Spherical Problem Definition.
From www.youtube.com
Worded Problem in Spherical Trigonometry YouTube Spherical Problem Definition One of the simplest theorems of spherical trigonometry to prove using plane trigonometry is the spherical law of cosines. In the spherical coordinate system, a point \(p\) in space (figure \(\pageindex{9}\)) is represented by the ordered triple \((ρ,θ,φ)\). Spherical coordinates are preferred over cartesian and cylindrical coordinates when the geometry of the problem exhibits spherical symmetry. Spherical geometry is the. Spherical Problem Definition.
From www.studocu.com
Spherical Aberration And Astigmatism Spherical Aberration And Spherical Problem Definition One of the simplest theorems of spherical trigonometry to prove using plane trigonometry is the spherical law of cosines. Spherical coordinates are preferred over cartesian and cylindrical coordinates when the geometry of the problem exhibits spherical symmetry. One of two standard non euclidean geometries. In the spherical coordinate system, a point \(p\) in space (figure \(\pageindex{9}\)) is represented by the. Spherical Problem Definition.
From www.slideserve.com
PPT Spherical Mirrors PowerPoint Presentation, free download ID3198821 Spherical Problem Definition Legendre polynomials appear in many different mathematical and physical situations: They originate as solutions of the. In the spherical coordinate system, a point \(p\) in space (figure \(\pageindex{9}\)) is represented by the ordered triple \((ρ,θ,φ)\). One of the simplest theorems of spherical trigonometry to prove using plane trigonometry is the spherical law of cosines. Spherical coordinates are preferred over cartesian. Spherical Problem Definition.
From www.researchgate.net
The spherical geometry problem Download Scientific Diagram Spherical Problem Definition One of two standard non euclidean geometries. Legendre polynomials appear in many different mathematical and physical situations: One of the simplest theorems of spherical trigonometry to prove using plane trigonometry is the spherical law of cosines. They originate as solutions of the. In the spherical coordinate system, a point \(p\) in space (figure \(\pageindex{9}\)) is represented by the ordered triple. Spherical Problem Definition.
From mathinsight.org
Spherical coordinates Math Insight Spherical Problem Definition Hyperbolic geometry became fashionable because thurston started it. Legendre polynomials appear in many different mathematical and physical situations: The solutions of the angular parts of the problem are often combined into one function of two variables, as problems with spherical symmetry arise often, leaving. This geometry has applications in cartography, navigation, and astronomy. They originate as solutions of the. Spherical. Spherical Problem Definition.
From www.researchgate.net
Schematic of the spherical geometry of the problem Download Spherical Problem Definition Spherical geometry works similarly to. Legendre polynomials appear in many different mathematical and physical situations: In the spherical coordinate system, a point \(p\) in space (figure \(\pageindex{9}\)) is represented by the ordered triple \((ρ,θ,φ)\). They originate as solutions of the. Spherical coordinates are preferred over cartesian and cylindrical coordinates when the geometry of the problem exhibits spherical symmetry. The solutions. Spherical Problem Definition.
From www.math-principles.com
Math Principles Spherical Zone Problems, 2 Spherical Problem Definition Spherical geometry works similarly to. Spherical geometry is the study of geometric objects located on the surface of a sphere. Spherical geometry studies the surface of a unit sphere. The solutions of the angular parts of the problem are often combined into one function of two variables, as problems with spherical symmetry arise often, leaving. Legendre polynomials appear in many. Spherical Problem Definition.
From www.researchgate.net
Definition of spherical coordinates θ (co‐latitude) and ϕ (azimuth) in Spherical Problem Definition The solutions of the angular parts of the problem are often combined into one function of two variables, as problems with spherical symmetry arise often, leaving. Hyperbolic geometry became fashionable because thurston started it. Spherical geometry is the study of geometric objects located on the surface of a sphere. Spherical geometry studies the surface of a unit sphere. One of. Spherical Problem Definition.
From www.geeksforgeeks.org
Spherical Mirrors Definition, Types, Image Formation, Uses & FAQs Spherical Problem Definition They originate as solutions of the. Legendre polynomials appear in many different mathematical and physical situations: Hyperbolic geometry became fashionable because thurston started it. The solutions of the angular parts of the problem are often combined into one function of two variables, as problems with spherical symmetry arise often, leaving. One of the simplest theorems of spherical trigonometry to prove. Spherical Problem Definition.
From www.researchgate.net
Problem definition of a spherical cavity in nonhomogeneous clays Spherical Problem Definition This geometry has applications in cartography, navigation, and astronomy. One of two standard non euclidean geometries. One of the simplest theorems of spherical trigonometry to prove using plane trigonometry is the spherical law of cosines. Spherical geometry studies the surface of a unit sphere. Spherical coordinates are preferred over cartesian and cylindrical coordinates when the geometry of the problem exhibits. Spherical Problem Definition.
From mathsathome.com
How to Calculate the Volume of a Spherical Cap Spherical Problem Definition Spherical geometry is the study of geometric objects located on the surface of a sphere. This geometry has applications in cartography, navigation, and astronomy. The solutions of the angular parts of the problem are often combined into one function of two variables, as problems with spherical symmetry arise often, leaving. Hyperbolic geometry became fashionable because thurston started it. They originate. Spherical Problem Definition.
From www.myopiaprofile.com
Understanding spherical aberration Myopia Profile Spherical Problem Definition Spherical geometry studies the surface of a unit sphere. Legendre polynomials appear in many different mathematical and physical situations: Spherical geometry works similarly to. They originate as solutions of the. One of the simplest theorems of spherical trigonometry to prove using plane trigonometry is the spherical law of cosines. Spherical geometry is the study of geometric objects located on the. Spherical Problem Definition.
From www.researchgate.net
Infinite medium with spherical hole in uniaxial tension (a) Problem Spherical Problem Definition This geometry has applications in cartography, navigation, and astronomy. Hyperbolic geometry became fashionable because thurston started it. One of the simplest theorems of spherical trigonometry to prove using plane trigonometry is the spherical law of cosines. The solutions of the angular parts of the problem are often combined into one function of two variables, as problems with spherical symmetry arise. Spherical Problem Definition.
From gioitkdio.blob.core.windows.net
Spherical View Definition at David Lamar blog Spherical Problem Definition Spherical geometry is the study of geometric objects located on the surface of a sphere. The solutions of the angular parts of the problem are often combined into one function of two variables, as problems with spherical symmetry arise often, leaving. Spherical geometry works similarly to. Hyperbolic geometry became fashionable because thurston started it. Legendre polynomials appear in many different. Spherical Problem Definition.
From ms.copernicus.org
MS Dimensional synthesis of a spherical linkage crank slider Spherical Problem Definition Spherical geometry works similarly to. The solutions of the angular parts of the problem are often combined into one function of two variables, as problems with spherical symmetry arise often, leaving. Spherical coordinates are preferred over cartesian and cylindrical coordinates when the geometry of the problem exhibits spherical symmetry. Spherical geometry studies the surface of a unit sphere. This geometry. Spherical Problem Definition.