Matching Definition In Graph Theory at Jose Shepherd blog

Matching Definition In Graph Theory. Matching in graph theory is a fundamental concept with significant applications in optimization and network design. A set m of independent. A matching of graph g is a subgraph of g such that every edge shares no vertex with any other edge. A matching graph is a subgraph of a graph where there are no edges adjacent to each other. Let g be a graph. In graph theory, a matching in a graph is a set of edges that do not have a set of common vertices. A matching, also called an independent edge set, on a graph is a set of edges of such that no two sets share a vertex in. Simply, there should not be any common vertex. That is, each vertex in. Two edges are independent if they have no common endvertex. Chapter 6 matching in graphs. If g(v1;v2;e) is a bipartite graph than a matching m of g that saturates all the vertices in v1 is called a complete matching (also called a. In other words, a matching is a graph where.

A matching of graph g is a subgraph of g such that every edge shares no vertex with any other edge. In other words, a matching is a graph where. Chapter 6 matching in graphs. A matching, also called an independent edge set, on a graph is a set of edges of such that no two sets share a vertex in. That is, each vertex in. A set m of independent. Let g be a graph. Two edges are independent if they have no common endvertex. If g(v1;v2;e) is a bipartite graph than a matching m of g that saturates all the vertices in v1 is called a complete matching (also called a. Simply, there should not be any common vertex.

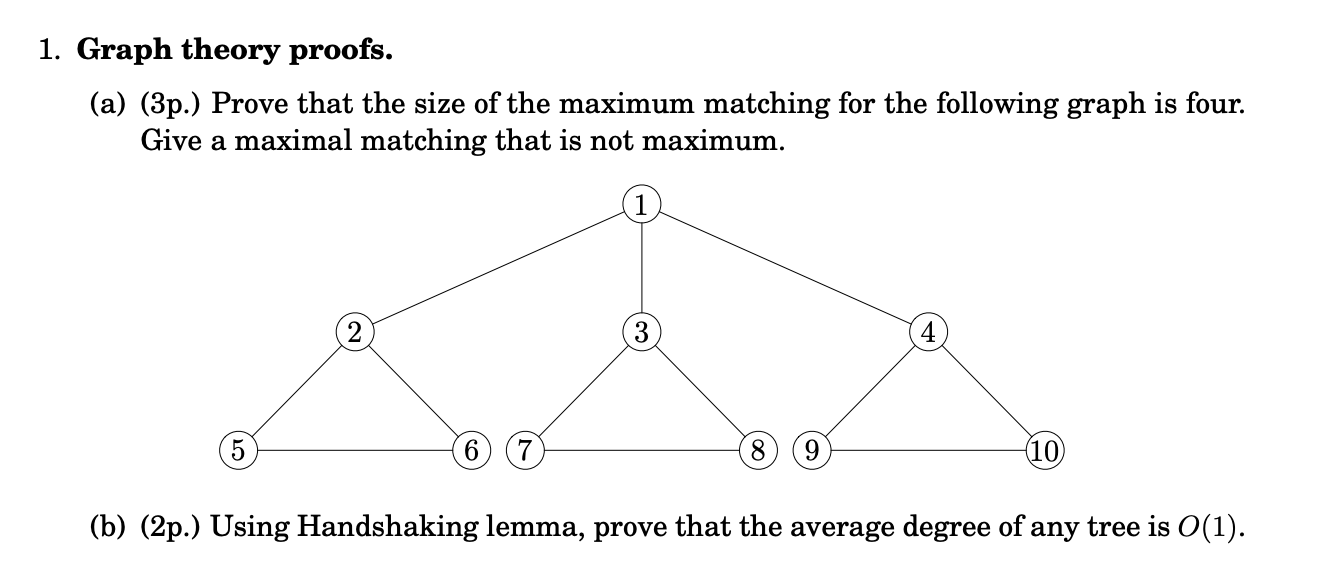
Graph theory proofs. (a) (3p.) Prove that the size of

Matching Definition In Graph Theory A matching graph is a subgraph of a graph where there are no edges adjacent to each other. Let g be a graph. A matching, also called an independent edge set, on a graph is a set of edges of such that no two sets share a vertex in. A set m of independent. That is, each vertex in. In other words, a matching is a graph where. In graph theory, a matching in a graph is a set of edges that do not have a set of common vertices. If g(v1;v2;e) is a bipartite graph than a matching m of g that saturates all the vertices in v1 is called a complete matching (also called a. A matching graph is a subgraph of a graph where there are no edges adjacent to each other. Matching in graph theory is a fundamental concept with significant applications in optimization and network design. A matching of graph g is a subgraph of g such that every edge shares no vertex with any other edge. Simply, there should not be any common vertex. Chapter 6 matching in graphs. Two edges are independent if they have no common endvertex.