What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0) . (2) express the distance in terms of x and y. Langrange multipliers let you find the maximum and/or minimum of a function given a function as a constraint on your input. Take a point $(x, y)$ on the curve, calculate its distance from $(2, 0)$. The fact that the point is on the curve allows you to express that. In this video we use calculus to find the minimum distance between a curve and point (in this. (1) let d denote the distance from a point (x, y) on the graph to the on given point (0, 2). To find the minimum distance from the curve y = (x − 2) 3 to the point (1, 0), we need to find the shortest distance bet.
from www.youtube.com
Take a point $(x, y)$ on the curve, calculate its distance from $(2, 0)$. In this video we use calculus to find the minimum distance between a curve and point (in this. (2) express the distance in terms of x and y. To find the minimum distance from the curve y = (x − 2) 3 to the point (1, 0), we need to find the shortest distance bet. Langrange multipliers let you find the maximum and/or minimum of a function given a function as a constraint on your input. The fact that the point is on the curve allows you to express that. (1) let d denote the distance from a point (x, y) on the graph to the on given point (0, 2).
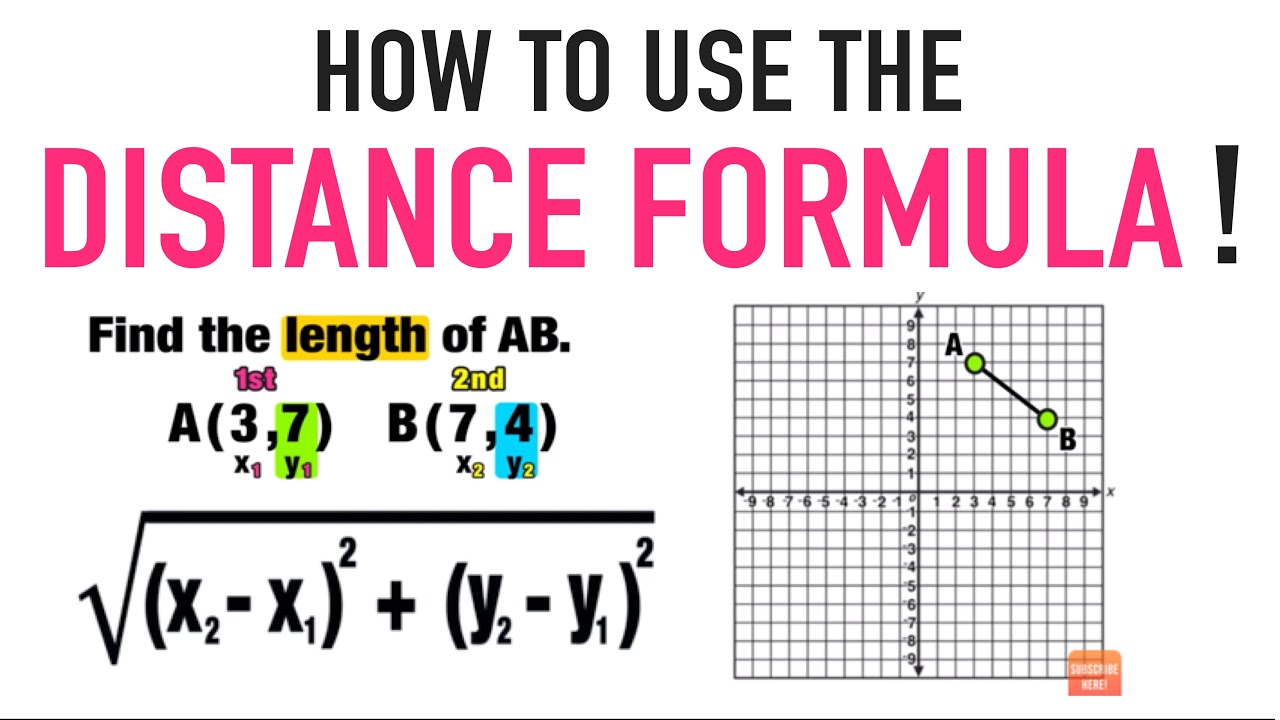
Using Distance Formula to Find Distance Between Two Points! YouTube
What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0) The fact that the point is on the curve allows you to express that. (2) express the distance in terms of x and y. To find the minimum distance from the curve y = (x − 2) 3 to the point (1, 0), we need to find the shortest distance bet. Langrange multipliers let you find the maximum and/or minimum of a function given a function as a constraint on your input. The fact that the point is on the curve allows you to express that. (1) let d denote the distance from a point (x, y) on the graph to the on given point (0, 2). Take a point $(x, y)$ on the curve, calculate its distance from $(2, 0)$. In this video we use calculus to find the minimum distance between a curve and point (in this.
From www.youtube.com
How to Find the Distance Between Two Points How to Use the Distance Formula YouTube What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0) Take a point $(x, y)$ on the curve, calculate its distance from $(2, 0)$. (2) express the distance in terms of x and y. Langrange multipliers let you find the maximum and/or minimum of a function given a function as a constraint on your input. (1) let d denote the distance from a point (x, y) on the graph to. What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0).
From www.youtube.com
Optimization Find The Minimum Distance Between Two Graphs YouTube What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0) Take a point $(x, y)$ on the curve, calculate its distance from $(2, 0)$. Langrange multipliers let you find the maximum and/or minimum of a function given a function as a constraint on your input. (2) express the distance in terms of x and y. (1) let d denote the distance from a point (x, y) on the graph to. What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0).
From www.chegg.com
Solved Find the absolute maximum and minimum values of the What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0) Langrange multipliers let you find the maximum and/or minimum of a function given a function as a constraint on your input. To find the minimum distance from the curve y = (x − 2) 3 to the point (1, 0), we need to find the shortest distance bet. The fact that the point is on the curve allows you to. What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0).
From www.toppr.com
"The minimum distance of any point on the ellipse ( x^{2}+3 y^{2}+4 x y= ) 4 from its centre isn What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0) Langrange multipliers let you find the maximum and/or minimum of a function given a function as a constraint on your input. (1) let d denote the distance from a point (x, y) on the graph to the on given point (0, 2). (2) express the distance in terms of x and y. The fact that the point is on the. What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0).
From www.doubtnut.com
The normal at the point (1,1) on the curve 2y+x^2=3is (A) x + y = 0 What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0) In this video we use calculus to find the minimum distance between a curve and point (in this. Take a point $(x, y)$ on the curve, calculate its distance from $(2, 0)$. (2) express the distance in terms of x and y. Langrange multipliers let you find the maximum and/or minimum of a function given a function as a constraint. What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0).
From www.nagwa.com
Question Video Finding the Coordinates of the Intersection Point between a Straight Line and a What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0) The fact that the point is on the curve allows you to express that. Take a point $(x, y)$ on the curve, calculate its distance from $(2, 0)$. Langrange multipliers let you find the maximum and/or minimum of a function given a function as a constraint on your input. To find the minimum distance from the curve y = (x. What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0).
From www.chegg.com
Solved In this project you will find the minimum distance What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0) (1) let d denote the distance from a point (x, y) on the graph to the on given point (0, 2). To find the minimum distance from the curve y = (x − 2) 3 to the point (1, 0), we need to find the shortest distance bet. Take a point $(x, y)$ on the curve, calculate its distance from. What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0).
From www.youtube.com
§3.6 Optimization Minimum Distance from a Point to a Curve YouTube What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0) To find the minimum distance from the curve y = (x − 2) 3 to the point (1, 0), we need to find the shortest distance bet. (2) express the distance in terms of x and y. Take a point $(x, y)$ on the curve, calculate its distance from $(2, 0)$. (1) let d denote the distance from a point. What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0).
From www.youtube.com
FIND THE EQUATIONS OF LINES PASSING THROUGH ONE POINT AND TWO POINTS YouTube What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0) Take a point $(x, y)$ on the curve, calculate its distance from $(2, 0)$. (1) let d denote the distance from a point (x, y) on the graph to the on given point (0, 2). The fact that the point is on the curve allows you to express that. (2) express the distance in terms of x and y. Langrange. What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0).
From courses.lumenlearning.com
Graphing Linear Equations Beginning Algebra What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0) (1) let d denote the distance from a point (x, y) on the graph to the on given point (0, 2). Langrange multipliers let you find the maximum and/or minimum of a function given a function as a constraint on your input. In this video we use calculus to find the minimum distance between a curve and point (in this.. What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0).
From www.chegg.com
Solved Find the minimum distance from the point (3,0,8) to What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0) Langrange multipliers let you find the maximum and/or minimum of a function given a function as a constraint on your input. In this video we use calculus to find the minimum distance between a curve and point (in this. The fact that the point is on the curve allows you to express that. (1) let d denote the distance from. What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0).
From mathsathome.com
How to Find the Vector Between Two Points What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0) To find the minimum distance from the curve y = (x − 2) 3 to the point (1, 0), we need to find the shortest distance bet. The fact that the point is on the curve allows you to express that. In this video we use calculus to find the minimum distance between a curve and point (in this. (2). What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0).
From www.reddit.com
[Mechanics] finding the minimum horizontal distance. r/PhysicsStudents What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0) The fact that the point is on the curve allows you to express that. (2) express the distance in terms of x and y. To find the minimum distance from the curve y = (x − 2) 3 to the point (1, 0), we need to find the shortest distance bet. Take a point $(x, y)$ on the curve, calculate. What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0).
From www.youtube.com
DISTANCE FORMULA STD 10th (GEOMETRY) CHAPTER 5 COORDINATE GEOMETRY YouTube What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0) Take a point $(x, y)$ on the curve, calculate its distance from $(2, 0)$. The fact that the point is on the curve allows you to express that. To find the minimum distance from the curve y = (x − 2) 3 to the point (1, 0), we need to find the shortest distance bet. (2) express the distance in. What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0).
From www.chegg.com
Solved EXAMPLE 5 Find the shortest distance from the point What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0) (1) let d denote the distance from a point (x, y) on the graph to the on given point (0, 2). To find the minimum distance from the curve y = (x − 2) 3 to the point (1, 0), we need to find the shortest distance bet. Langrange multipliers let you find the maximum and/or minimum of a function. What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0).
From www.youtube.com
How to find Minimum Distance from a point to the Curve Application Derivatives MCV Calculus What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0) Take a point $(x, y)$ on the curve, calculate its distance from $(2, 0)$. In this video we use calculus to find the minimum distance between a curve and point (in this. Langrange multipliers let you find the maximum and/or minimum of a function given a function as a constraint on your input. (1) let d denote the distance from. What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0).
From www.tessshebaylo.com
Equation Of Parabola Between Two Points Tessshebaylo What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0) In this video we use calculus to find the minimum distance between a curve and point (in this. Langrange multipliers let you find the maximum and/or minimum of a function given a function as a constraint on your input. (2) express the distance in terms of x and y. Take a point $(x, y)$ on the curve, calculate its distance. What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0).
From www.youtube.com
Find the Point closest to 0, 3 on curve x^2 = 2y IIT JEE GATE Calculus YouTube What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0) The fact that the point is on the curve allows you to express that. To find the minimum distance from the curve y = (x − 2) 3 to the point (1, 0), we need to find the shortest distance bet. Take a point $(x, y)$ on the curve, calculate its distance from $(2, 0)$. (2) express the distance in. What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0).
From www.youtube.com
Using Distance Formula to Find Distance Between Two Points! YouTube What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0) In this video we use calculus to find the minimum distance between a curve and point (in this. To find the minimum distance from the curve y = (x − 2) 3 to the point (1, 0), we need to find the shortest distance bet. The fact that the point is on the curve allows you to express that. (2). What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0).
From www.chegg.com
Solved EXAMPLE 5 Find the shortest distance from the point What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0) To find the minimum distance from the curve y = (x − 2) 3 to the point (1, 0), we need to find the shortest distance bet. Langrange multipliers let you find the maximum and/or minimum of a function given a function as a constraint on your input. In this video we use calculus to find the minimum distance between. What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0).
From www.chegg.com
Solved Find the minimum distance from the point (3,0,8) to What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0) The fact that the point is on the curve allows you to express that. In this video we use calculus to find the minimum distance between a curve and point (in this. (2) express the distance in terms of x and y. To find the minimum distance from the curve y = (x − 2) 3 to the point (1,. What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0).
From www.youtube.com
Optimization Find the minimum distance from a point to a function YouTube What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0) (2) express the distance in terms of x and y. Take a point $(x, y)$ on the curve, calculate its distance from $(2, 0)$. The fact that the point is on the curve allows you to express that. (1) let d denote the distance from a point (x, y) on the graph to the on given point (0, 2). In. What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0).
From www.chegg.com
Solved (1 point) Find the minimum distance from the cone What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0) The fact that the point is on the curve allows you to express that. (1) let d denote the distance from a point (x, y) on the graph to the on given point (0, 2). To find the minimum distance from the curve y = (x − 2) 3 to the point (1, 0), we need to find the shortest. What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0).
From www.youtube.com
minimum distance between the point and the plane (KristaKingMath) YouTube What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0) Langrange multipliers let you find the maximum and/or minimum of a function given a function as a constraint on your input. To find the minimum distance from the curve y = (x − 2) 3 to the point (1, 0), we need to find the shortest distance bet. In this video we use calculus to find the minimum distance between. What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0).
From www.youtube.com
The Distance Formula Finding the Distance Between Two Points YouTube What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0) (1) let d denote the distance from a point (x, y) on the graph to the on given point (0, 2). The fact that the point is on the curve allows you to express that. Langrange multipliers let you find the maximum and/or minimum of a function given a function as a constraint on your input. (2) express the distance. What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0).
From science.howstuffworks.com
Distance Formula Finding the Distance Between Two Points HowStuffWorks What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0) (2) express the distance in terms of x and y. To find the minimum distance from the curve y = (x − 2) 3 to the point (1, 0), we need to find the shortest distance bet. Take a point $(x, y)$ on the curve, calculate its distance from $(2, 0)$. (1) let d denote the distance from a point. What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0).
From youtube.com
Plotting Points on the Coordinate Plane YouTube What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0) Langrange multipliers let you find the maximum and/or minimum of a function given a function as a constraint on your input. Take a point $(x, y)$ on the curve, calculate its distance from $(2, 0)$. The fact that the point is on the curve allows you to express that. In this video we use calculus to find the minimum distance. What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0).
From saylordotorg.github.io
Quadratic Functions and Their Graphs What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0) Take a point $(x, y)$ on the curve, calculate its distance from $(2, 0)$. In this video we use calculus to find the minimum distance between a curve and point (in this. (1) let d denote the distance from a point (x, y) on the graph to the on given point (0, 2). Langrange multipliers let you find the maximum. What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0).
From haipernews.com
How To Calculate Distance From X And Y Coordinates Haiper What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0) To find the minimum distance from the curve y = (x − 2) 3 to the point (1, 0), we need to find the shortest distance bet. (1) let d denote the distance from a point (x, y) on the graph to the on given point (0, 2). Take a point $(x, y)$ on the curve, calculate its distance from. What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0).
From www.numerade.com
SOLVED Find the geodesic the shortest distance between two points on the surface of a sphere What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0) (1) let d denote the distance from a point (x, y) on the graph to the on given point (0, 2). To find the minimum distance from the curve y = (x − 2) 3 to the point (1, 0), we need to find the shortest distance bet. The fact that the point is on the curve allows you to. What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0).
From www.chegg.com
Solved Find the minimum distance from the parabola x y^2 What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0) To find the minimum distance from the curve y = (x − 2) 3 to the point (1, 0), we need to find the shortest distance bet. In this video we use calculus to find the minimum distance between a curve and point (in this. The fact that the point is on the curve allows you to express that. Take. What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0).
From www.ck12.org
Circles in the Coordinate Plane ( Read ) Geometry CK12 Foundation What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0) To find the minimum distance from the curve y = (x − 2) 3 to the point (1, 0), we need to find the shortest distance bet. (2) express the distance in terms of x and y. The fact that the point is on the curve allows you to express that. Take a point $(x, y)$ on the curve, calculate. What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0).
From www.youtube.com
The Distance Formula Examples YouTube What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0) (1) let d denote the distance from a point (x, y) on the graph to the on given point (0, 2). In this video we use calculus to find the minimum distance between a curve and point (in this. To find the minimum distance from the curve y = (x − 2) 3 to the point (1, 0), we need. What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0).
From thirdspacelearning.com
Distance Formula GCSE Maths Steps, Examples & Worksheet What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0) To find the minimum distance from the curve y = (x − 2) 3 to the point (1, 0), we need to find the shortest distance bet. Langrange multipliers let you find the maximum and/or minimum of a function given a function as a constraint on your input. Take a point $(x, y)$ on the curve, calculate its distance from. What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0).
From www.wikihow.com
How to Find the Distance Between Two Points 6 Steps What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0) (2) express the distance in terms of x and y. The fact that the point is on the curve allows you to express that. Take a point $(x, y)$ on the curve, calculate its distance from $(2, 0)$. (1) let d denote the distance from a point (x, y) on the graph to the on given point (0, 2). Langrange. What Is The Minimum Distance From Y=(X-2)^3 To The Point (1 0).