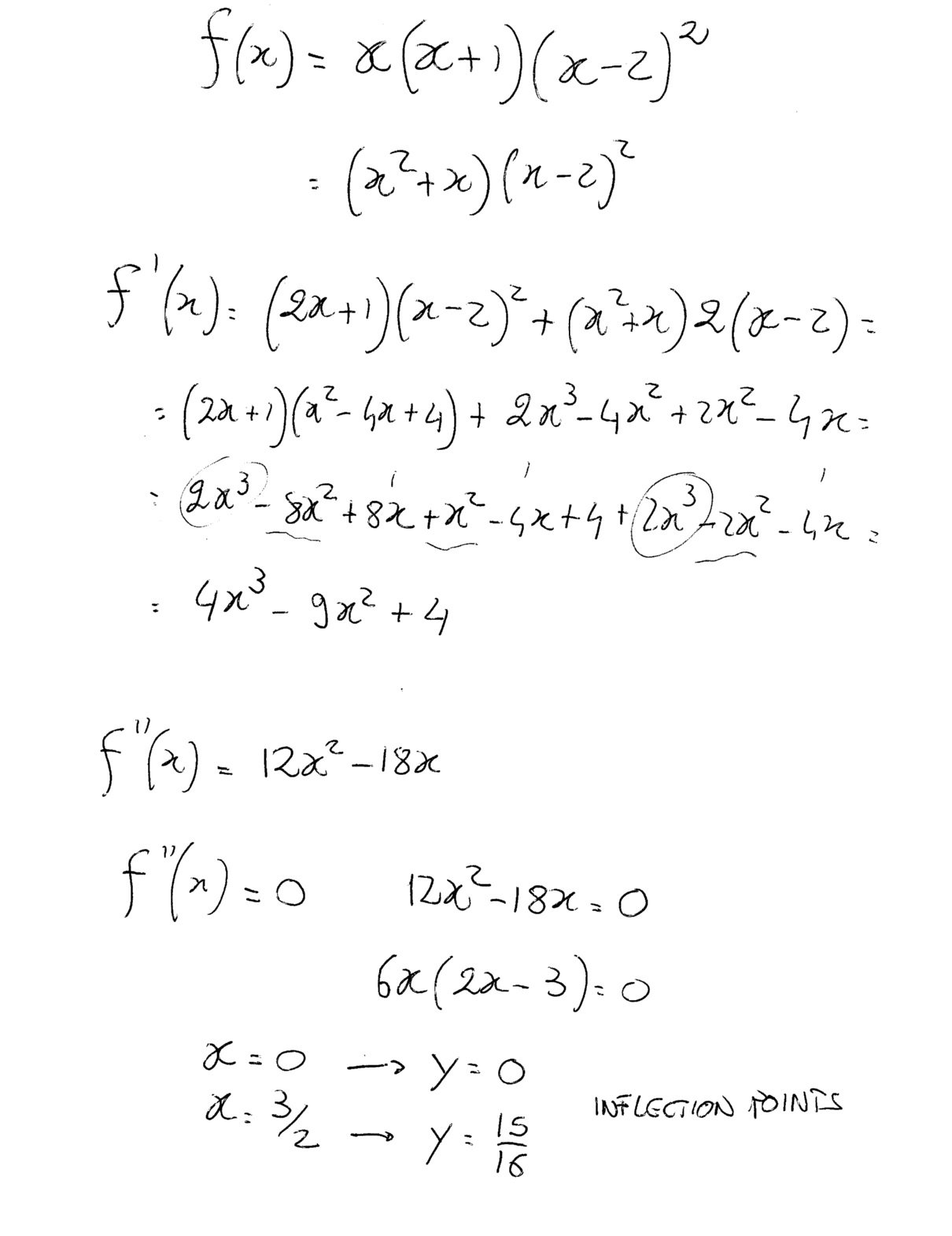Point Of Inflection 1/X . When the second derivative is negative, the function is concave downward. The point of inflection or inflection point is a point in which the concavity of the function changes. It means that the function changes from. This means that a point of inflection is a point where the second derivative changes. A point of inflection is any point at which a curve changes from being convex to being concave. And the inflection point is where it goes from concave upward to concave downward (or vice versa). For a function \ (f (x),\) its concavity can be measured by its second order derivative \ (f'' (x).\) when \. An inflection point occurs when the sign of the second derivative of a function, f (x), changes from positive to negative (or vice versa) at a point where f (x) = 0 or undefined. A curve's inflection point is the point at which the curve's concavity changes.
from socratic.org
When the second derivative is negative, the function is concave downward. It means that the function changes from. A curve's inflection point is the point at which the curve's concavity changes. The point of inflection or inflection point is a point in which the concavity of the function changes. And the inflection point is where it goes from concave upward to concave downward (or vice versa). For a function \ (f (x),\) its concavity can be measured by its second order derivative \ (f'' (x).\) when \. An inflection point occurs when the sign of the second derivative of a function, f (x), changes from positive to negative (or vice versa) at a point where f (x) = 0 or undefined. A point of inflection is any point at which a curve changes from being convex to being concave. This means that a point of inflection is a point where the second derivative changes.
If f " (x) = x(x+1)(x2)^2, what are the xcoordinates of the points of
Point Of Inflection 1/X And the inflection point is where it goes from concave upward to concave downward (or vice versa). It means that the function changes from. A point of inflection is any point at which a curve changes from being convex to being concave. The point of inflection or inflection point is a point in which the concavity of the function changes. For a function \ (f (x),\) its concavity can be measured by its second order derivative \ (f'' (x).\) when \. An inflection point occurs when the sign of the second derivative of a function, f (x), changes from positive to negative (or vice versa) at a point where f (x) = 0 or undefined. And the inflection point is where it goes from concave upward to concave downward (or vice versa). This means that a point of inflection is a point where the second derivative changes. A curve's inflection point is the point at which the curve's concavity changes. When the second derivative is negative, the function is concave downward.
From socratic.org
If f " (x) = x(x+1)(x2)^2, what are the xcoordinates of the points of Point Of Inflection 1/X When the second derivative is negative, the function is concave downward. An inflection point occurs when the sign of the second derivative of a function, f (x), changes from positive to negative (or vice versa) at a point where f (x) = 0 or undefined. And the inflection point is where it goes from concave upward to concave downward (or. Point Of Inflection 1/X.
From www.easysevens.com
Derivatives Local Maximum, Minimum and Point of Inflection Point Of Inflection 1/X The point of inflection or inflection point is a point in which the concavity of the function changes. And the inflection point is where it goes from concave upward to concave downward (or vice versa). An inflection point occurs when the sign of the second derivative of a function, f (x), changes from positive to negative (or vice versa) at. Point Of Inflection 1/X.
From studylib.net
Point of inflection Point Of Inflection 1/X An inflection point occurs when the sign of the second derivative of a function, f (x), changes from positive to negative (or vice versa) at a point where f (x) = 0 or undefined. For a function \ (f (x),\) its concavity can be measured by its second order derivative \ (f'' (x).\) when \. And the inflection point is. Point Of Inflection 1/X.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Point Of Inflection 1/X For a function \ (f (x),\) its concavity can be measured by its second order derivative \ (f'' (x).\) when \. The point of inflection or inflection point is a point in which the concavity of the function changes. And the inflection point is where it goes from concave upward to concave downward (or vice versa). It means that the. Point Of Inflection 1/X.
From www.numerade.com
SOLVEDShow that a cubic function (a thirddegree polynomial) always Point Of Inflection 1/X When the second derivative is negative, the function is concave downward. For a function \ (f (x),\) its concavity can be measured by its second order derivative \ (f'' (x).\) when \. A curve's inflection point is the point at which the curve's concavity changes. This means that a point of inflection is a point where the second derivative changes.. Point Of Inflection 1/X.
From www.numerade.com
SOLVED On the graph of the function below, identify all extrema (local Point Of Inflection 1/X When the second derivative is negative, the function is concave downward. It means that the function changes from. For a function \ (f (x),\) its concavity can be measured by its second order derivative \ (f'' (x).\) when \. A point of inflection is any point at which a curve changes from being convex to being concave. An inflection point. Point Of Inflection 1/X.
From www.chegg.com
Solved (1 point) Use a graph below of f(x) = 3e9x2 to Point Of Inflection 1/X An inflection point occurs when the sign of the second derivative of a function, f (x), changes from positive to negative (or vice versa) at a point where f (x) = 0 or undefined. When the second derivative is negative, the function is concave downward. A curve's inflection point is the point at which the curve's concavity changes. For a. Point Of Inflection 1/X.
From www.youtube.com
Number of points of inflection of curve `y = (x2)^6(x3)^5` is YouTube Point Of Inflection 1/X An inflection point occurs when the sign of the second derivative of a function, f (x), changes from positive to negative (or vice versa) at a point where f (x) = 0 or undefined. A curve's inflection point is the point at which the curve's concavity changes. For a function \ (f (x),\) its concavity can be measured by its. Point Of Inflection 1/X.
From www.chegg.com
Solved State the xcoordinates of the inflection points of Point Of Inflection 1/X An inflection point occurs when the sign of the second derivative of a function, f (x), changes from positive to negative (or vice versa) at a point where f (x) = 0 or undefined. It means that the function changes from. And the inflection point is where it goes from concave upward to concave downward (or vice versa). For a. Point Of Inflection 1/X.
From math.stackexchange.com
real analysis Reconstructing a function from its critical points and Point Of Inflection 1/X A curve's inflection point is the point at which the curve's concavity changes. When the second derivative is negative, the function is concave downward. It means that the function changes from. A point of inflection is any point at which a curve changes from being convex to being concave. The point of inflection or inflection point is a point in. Point Of Inflection 1/X.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Point Of Inflection 1/X A curve's inflection point is the point at which the curve's concavity changes. When the second derivative is negative, the function is concave downward. It means that the function changes from. A point of inflection is any point at which a curve changes from being convex to being concave. This means that a point of inflection is a point where. Point Of Inflection 1/X.
From www.mashupmath.com
How to Graph a Function in 3 Easy Steps — Mashup Math Point Of Inflection 1/X When the second derivative is negative, the function is concave downward. A curve's inflection point is the point at which the curve's concavity changes. It means that the function changes from. For a function \ (f (x),\) its concavity can be measured by its second order derivative \ (f'' (x).\) when \. A point of inflection is any point at. Point Of Inflection 1/X.
From www.radfordmathematics.com
Point of Inflection Calculus Point Of Inflection 1/X This means that a point of inflection is a point where the second derivative changes. It means that the function changes from. The point of inflection or inflection point is a point in which the concavity of the function changes. And the inflection point is where it goes from concave upward to concave downward (or vice versa). When the second. Point Of Inflection 1/X.
From www.chegg.com
Solved Based on the above graph of the second derivative of Point Of Inflection 1/X An inflection point occurs when the sign of the second derivative of a function, f (x), changes from positive to negative (or vice versa) at a point where f (x) = 0 or undefined. When the second derivative is negative, the function is concave downward. A point of inflection is any point at which a curve changes from being convex. Point Of Inflection 1/X.
From www.youtube.com
Find intervals of concavity, inflection points, increasing decreasing Point Of Inflection 1/X This means that a point of inflection is a point where the second derivative changes. It means that the function changes from. And the inflection point is where it goes from concave upward to concave downward (or vice versa). An inflection point occurs when the sign of the second derivative of a function, f (x), changes from positive to negative. Point Of Inflection 1/X.
From www.chegg.com
Solved Find the points of inflection forf(x)=x4+8x36(0,6) Point Of Inflection 1/X It means that the function changes from. And the inflection point is where it goes from concave upward to concave downward (or vice versa). An inflection point occurs when the sign of the second derivative of a function, f (x), changes from positive to negative (or vice versa) at a point where f (x) = 0 or undefined. The point. Point Of Inflection 1/X.
From www.researchgate.net
Pictorial representation of inflection1 approach considering one Point Of Inflection 1/X The point of inflection or inflection point is a point in which the concavity of the function changes. An inflection point occurs when the sign of the second derivative of a function, f (x), changes from positive to negative (or vice versa) at a point where f (x) = 0 or undefined. For a function \ (f (x),\) its concavity. Point Of Inflection 1/X.
From socratic.org
How do you find all points of inflection for f(x) = (1/12)x^4 2x^2 Point Of Inflection 1/X An inflection point occurs when the sign of the second derivative of a function, f (x), changes from positive to negative (or vice versa) at a point where f (x) = 0 or undefined. It means that the function changes from. When the second derivative is negative, the function is concave downward. A point of inflection is any point at. Point Of Inflection 1/X.
From www.coursehero.com
[Solved] State the xcoordinates of the inflection points of the curve Point Of Inflection 1/X When the second derivative is negative, the function is concave downward. And the inflection point is where it goes from concave upward to concave downward (or vice versa). It means that the function changes from. A point of inflection is any point at which a curve changes from being convex to being concave. For a function \ (f (x),\) its. Point Of Inflection 1/X.
From socratic.org
What are the inflection points for (x^2)/(x^2+1)? Socratic Point Of Inflection 1/X A point of inflection is any point at which a curve changes from being convex to being concave. This means that a point of inflection is a point where the second derivative changes. And the inflection point is where it goes from concave upward to concave downward (or vice versa). The point of inflection or inflection point is a point. Point Of Inflection 1/X.
From londonstatus.co.uk
What Is The Non Stationary Point Of Inflection? London Status Point Of Inflection 1/X For a function \ (f (x),\) its concavity can be measured by its second order derivative \ (f'' (x).\) when \. It means that the function changes from. When the second derivative is negative, the function is concave downward. A curve's inflection point is the point at which the curve's concavity changes. And the inflection point is where it goes. Point Of Inflection 1/X.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Point Of Inflection 1/X The point of inflection or inflection point is a point in which the concavity of the function changes. For a function \ (f (x),\) its concavity can be measured by its second order derivative \ (f'' (x).\) when \. A curve's inflection point is the point at which the curve's concavity changes. This means that a point of inflection is. Point Of Inflection 1/X.
From www.numerade.com
SOLVEDAnalyze and sketch the graph of the function. Identify any Point Of Inflection 1/X For a function \ (f (x),\) its concavity can be measured by its second order derivative \ (f'' (x).\) when \. An inflection point occurs when the sign of the second derivative of a function, f (x), changes from positive to negative (or vice versa) at a point where f (x) = 0 or undefined. When the second derivative is. Point Of Inflection 1/X.
From www.mathsbook.de
Point d'inflexion Convexité Cours terminale ES Point Of Inflection 1/X The point of inflection or inflection point is a point in which the concavity of the function changes. This means that a point of inflection is a point where the second derivative changes. A point of inflection is any point at which a curve changes from being convex to being concave. And the inflection point is where it goes from. Point Of Inflection 1/X.
From www.nagwa.com
Question Video Finding the Inflection Points of a Function from the Point Of Inflection 1/X And the inflection point is where it goes from concave upward to concave downward (or vice versa). For a function \ (f (x),\) its concavity can be measured by its second order derivative \ (f'' (x).\) when \. A curve's inflection point is the point at which the curve's concavity changes. An inflection point occurs when the sign of the. Point Of Inflection 1/X.
From www.youtube.com
Point of Inflection Point of Inflexion f''(x)=0 Definition How Point Of Inflection 1/X This means that a point of inflection is a point where the second derivative changes. The point of inflection or inflection point is a point in which the concavity of the function changes. And the inflection point is where it goes from concave upward to concave downward (or vice versa). For a function \ (f (x),\) its concavity can be. Point Of Inflection 1/X.
From dawoum.tistory.com
(번역) Inflection point Point Of Inflection 1/X A point of inflection is any point at which a curve changes from being convex to being concave. This means that a point of inflection is a point where the second derivative changes. The point of inflection or inflection point is a point in which the concavity of the function changes. A curve's inflection point is the point at which. Point Of Inflection 1/X.
From www.youtube.com
Stationary point of inflection (Part 1) YouTube Point Of Inflection 1/X An inflection point occurs when the sign of the second derivative of a function, f (x), changes from positive to negative (or vice versa) at a point where f (x) = 0 or undefined. A curve's inflection point is the point at which the curve's concavity changes. And the inflection point is where it goes from concave upward to concave. Point Of Inflection 1/X.
From www.chegg.com
Solved State the xcoordinates of the inflection points of Point Of Inflection 1/X For a function \ (f (x),\) its concavity can be measured by its second order derivative \ (f'' (x).\) when \. And the inflection point is where it goes from concave upward to concave downward (or vice versa). This means that a point of inflection is a point where the second derivative changes. When the second derivative is negative, the. Point Of Inflection 1/X.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Point Of Inflection 1/X For a function \ (f (x),\) its concavity can be measured by its second order derivative \ (f'' (x).\) when \. A point of inflection is any point at which a curve changes from being convex to being concave. When the second derivative is negative, the function is concave downward. This means that a point of inflection is a point. Point Of Inflection 1/X.
From www.radfordmathematics.com
Point of Inflection Calculus Point Of Inflection 1/X This means that a point of inflection is a point where the second derivative changes. It means that the function changes from. The point of inflection or inflection point is a point in which the concavity of the function changes. When the second derivative is negative, the function is concave downward. For a function \ (f (x),\) its concavity can. Point Of Inflection 1/X.
From www.numerade.com
SOLVEDpoint) Determine the intervals on which the function f(x) = 3x2 Point Of Inflection 1/X For a function \ (f (x),\) its concavity can be measured by its second order derivative \ (f'' (x).\) when \. The point of inflection or inflection point is a point in which the concavity of the function changes. When the second derivative is negative, the function is concave downward. And the inflection point is where it goes from concave. Point Of Inflection 1/X.
From www.youtube.com
Points of Inflection from f(x)=cos(2x) YouTube Point Of Inflection 1/X An inflection point occurs when the sign of the second derivative of a function, f (x), changes from positive to negative (or vice versa) at a point where f (x) = 0 or undefined. This means that a point of inflection is a point where the second derivative changes. The point of inflection or inflection point is a point in. Point Of Inflection 1/X.
From www.youtube.com
Define inflection point l what is inflection point with example l Point Of Inflection 1/X It means that the function changes from. A curve's inflection point is the point at which the curve's concavity changes. An inflection point occurs when the sign of the second derivative of a function, f (x), changes from positive to negative (or vice versa) at a point where f (x) = 0 or undefined. When the second derivative is negative,. Point Of Inflection 1/X.
From www.chegg.com
Solved Consider the following graph of f(x). Use the slider Point Of Inflection 1/X An inflection point occurs when the sign of the second derivative of a function, f (x), changes from positive to negative (or vice versa) at a point where f (x) = 0 or undefined. A point of inflection is any point at which a curve changes from being convex to being concave. The point of inflection or inflection point is. Point Of Inflection 1/X.