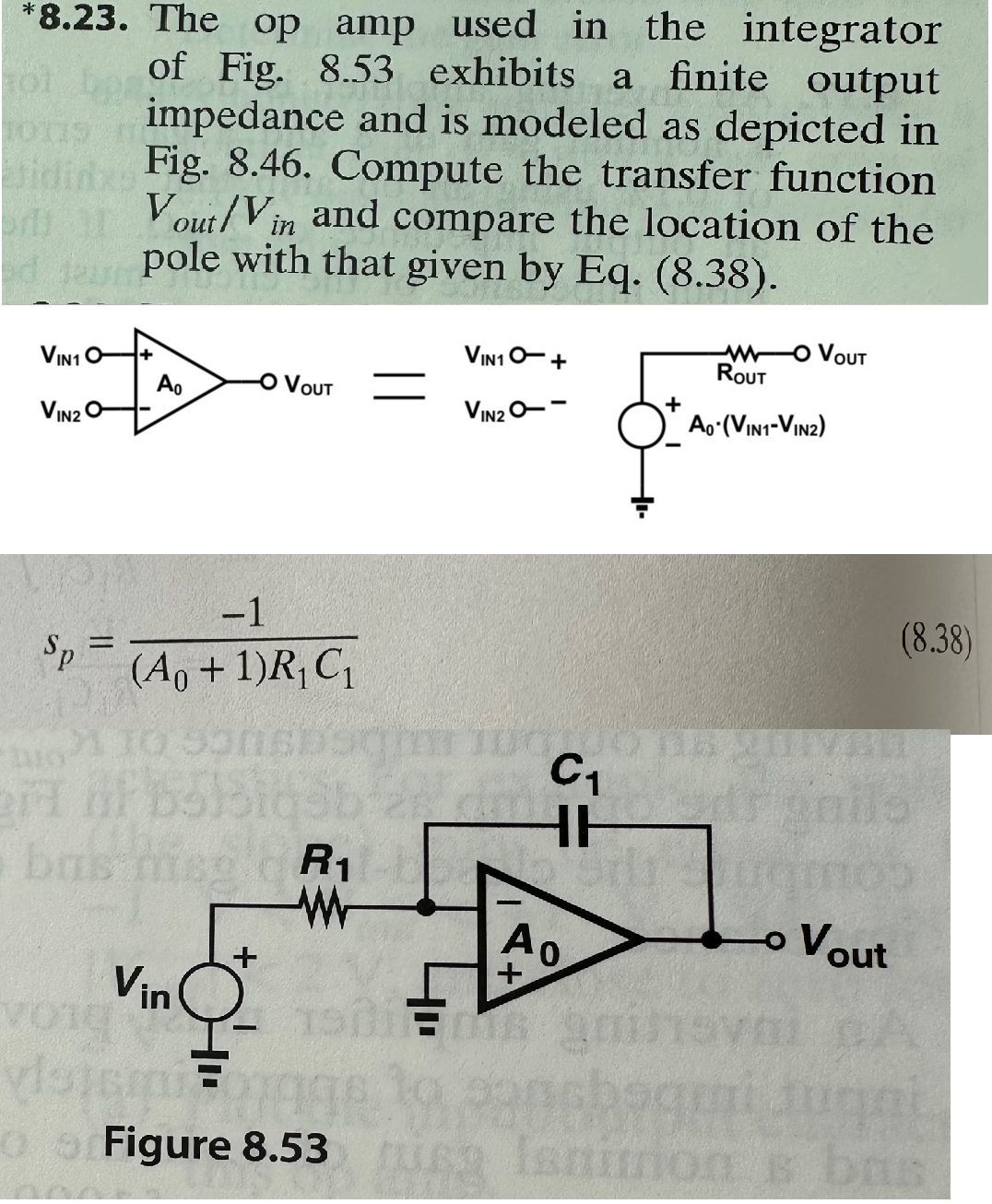
Transfer Function Vout/Vin . The transfer function h(s) of a circuit is defined as: The systematic approach is not to use canned formulas at all, but derive the transfer function from first principles. Transfer function of second order low pass filter. In a simple circuit like the following: In general, the transfer function \ ( h (s) \) of the cascaded circuit. The laplace domain transfer function, if properly derived, is vout/vin where vout and vin are the laplace transforms of. (1) how do you derive this function? H(s) = the transfer function of a circuit = transform of the output transform of the input. Vin = i1*r1 => i1 = vin / r1. I calculate the transfer function using i1 = i2:
from www.chegg.com
Transfer function of second order low pass filter. H(s) = the transfer function of a circuit = transform of the output transform of the input. Vin = i1*r1 => i1 = vin / r1. The transfer function h(s) of a circuit is defined as: The systematic approach is not to use canned formulas at all, but derive the transfer function from first principles. (1) how do you derive this function? In general, the transfer function \ ( h (s) \) of the cascaded circuit. In a simple circuit like the following: The laplace domain transfer function, if properly derived, is vout/vin where vout and vin are the laplace transforms of. I calculate the transfer function using i1 = i2:
Solved Compute the transfer function Vout/vin and compare
Transfer Function Vout/Vin In a simple circuit like the following: I calculate the transfer function using i1 = i2: (1) how do you derive this function? H(s) = the transfer function of a circuit = transform of the output transform of the input. The systematic approach is not to use canned formulas at all, but derive the transfer function from first principles. The laplace domain transfer function, if properly derived, is vout/vin where vout and vin are the laplace transforms of. Transfer function of second order low pass filter. In general, the transfer function \ ( h (s) \) of the cascaded circuit. In a simple circuit like the following: Vin = i1*r1 => i1 = vin / r1. The transfer function h(s) of a circuit is defined as:
From www.chegg.com
Solved 4. (20 pts) Plot the transfer function (Vout Vin) of Transfer Function Vout/Vin The systematic approach is not to use canned formulas at all, but derive the transfer function from first principles. The laplace domain transfer function, if properly derived, is vout/vin where vout and vin are the laplace transforms of. In a simple circuit like the following: The transfer function h(s) of a circuit is defined as: (1) how do you derive. Transfer Function Vout/Vin.
From www.chegg.com
Solved 3. Find the transfer function, vout / Vin, for the Transfer Function Vout/Vin The laplace domain transfer function, if properly derived, is vout/vin where vout and vin are the laplace transforms of. I calculate the transfer function using i1 = i2: Transfer function of second order low pass filter. The transfer function h(s) of a circuit is defined as: In a simple circuit like the following: The systematic approach is not to use. Transfer Function Vout/Vin.
From www.chegg.com
Solved Obtain the transfer function Vout(s)/Vin(s) of the Transfer Function Vout/Vin (1) how do you derive this function? The transfer function h(s) of a circuit is defined as: In general, the transfer function \ ( h (s) \) of the cascaded circuit. H(s) = the transfer function of a circuit = transform of the output transform of the input. In a simple circuit like the following: I calculate the transfer function. Transfer Function Vout/Vin.
From www.chegg.com
Solved 1. Find the transfer function Vout(s)/Vin(s). (10pt) Transfer Function Vout/Vin The transfer function h(s) of a circuit is defined as: In general, the transfer function \ ( h (s) \) of the cascaded circuit. The laplace domain transfer function, if properly derived, is vout/vin where vout and vin are the laplace transforms of. (1) how do you derive this function? The systematic approach is not to use canned formulas at. Transfer Function Vout/Vin.
From www.chegg.com
Solved Exercise 6.4 Derive an expression for the transfer Transfer Function Vout/Vin In a simple circuit like the following: (1) how do you derive this function? Transfer function of second order low pass filter. Vin = i1*r1 => i1 = vin / r1. The laplace domain transfer function, if properly derived, is vout/vin where vout and vin are the laplace transforms of. The transfer function h(s) of a circuit is defined as:. Transfer Function Vout/Vin.
From www.chegg.com
Solved Derive the transfer function H(W) = Vout/Vin for the Transfer Function Vout/Vin Transfer function of second order low pass filter. The systematic approach is not to use canned formulas at all, but derive the transfer function from first principles. (1) how do you derive this function? The laplace domain transfer function, if properly derived, is vout/vin where vout and vin are the laplace transforms of. In general, the transfer function \ (. Transfer Function Vout/Vin.
From www.chegg.com
Solved Find the transfer function, G(s) = Vout/Vin, of the Transfer Function Vout/Vin (1) how do you derive this function? The laplace domain transfer function, if properly derived, is vout/vin where vout and vin are the laplace transforms of. In a simple circuit like the following: I calculate the transfer function using i1 = i2: Transfer function of second order low pass filter. Vin = i1*r1 => i1 = vin / r1. H(s). Transfer Function Vout/Vin.
From www.chegg.com
Solved 1. Calculate the transfer function (H(s)= Vout / Vin Transfer Function Vout/Vin The transfer function h(s) of a circuit is defined as: Vin = i1*r1 => i1 = vin / r1. The systematic approach is not to use canned formulas at all, but derive the transfer function from first principles. Transfer function of second order low pass filter. I calculate the transfer function using i1 = i2: H(s) = the transfer function. Transfer Function Vout/Vin.
From www.chegg.com
Solved Find transfer function Vout(s)/Vin(s) of the Transfer Function Vout/Vin H(s) = the transfer function of a circuit = transform of the output transform of the input. Transfer function of second order low pass filter. The laplace domain transfer function, if properly derived, is vout/vin where vout and vin are the laplace transforms of. (1) how do you derive this function? I calculate the transfer function using i1 = i2:. Transfer Function Vout/Vin.
From www.chegg.com
Solved Compute the transfer function Vout/vin and compare Transfer Function Vout/Vin I calculate the transfer function using i1 = i2: The systematic approach is not to use canned formulas at all, but derive the transfer function from first principles. H(s) = the transfer function of a circuit = transform of the output transform of the input. Transfer function of second order low pass filter. The laplace domain transfer function, if properly. Transfer Function Vout/Vin.
From shirakawa-shienkai.or.jp
Atticus raket Verdeel first order low pass filter transfer function Transfer Function Vout/Vin The systematic approach is not to use canned formulas at all, but derive the transfer function from first principles. Vin = i1*r1 => i1 = vin / r1. I calculate the transfer function using i1 = i2: H(s) = the transfer function of a circuit = transform of the output transform of the input. In a simple circuit like the. Transfer Function Vout/Vin.
From www.numerade.com
The transfer function H(f) = Vout/Vin of a filter is shown in the Transfer Function Vout/Vin H(s) = the transfer function of a circuit = transform of the output transform of the input. I calculate the transfer function using i1 = i2: In general, the transfer function \ ( h (s) \) of the cascaded circuit. The systematic approach is not to use canned formulas at all, but derive the transfer function from first principles. The. Transfer Function Vout/Vin.
From www.chegg.com
Solved 1. A high pass filter is shown below. 27fc O + DERIVE Transfer Function Vout/Vin In a simple circuit like the following: The laplace domain transfer function, if properly derived, is vout/vin where vout and vin are the laplace transforms of. Transfer function of second order low pass filter. I calculate the transfer function using i1 = i2: Vin = i1*r1 => i1 = vin / r1. (1) how do you derive this function? H(s). Transfer Function Vout/Vin.
From electronics.stackexchange.com
capacitor how to find Vout/Vin in this circuit? BJT frequency Transfer Function Vout/Vin Vin = i1*r1 => i1 = vin / r1. Transfer function of second order low pass filter. I calculate the transfer function using i1 = i2: (1) how do you derive this function? The laplace domain transfer function, if properly derived, is vout/vin where vout and vin are the laplace transforms of. The transfer function h(s) of a circuit is. Transfer Function Vout/Vin.
From www.chegg.com
Solved 1. Plot the transfer function Vout Vs. Vin for the Transfer Function Vout/Vin Transfer function of second order low pass filter. Vin = i1*r1 => i1 = vin / r1. The laplace domain transfer function, if properly derived, is vout/vin where vout and vin are the laplace transforms of. I calculate the transfer function using i1 = i2: H(s) = the transfer function of a circuit = transform of the output transform of. Transfer Function Vout/Vin.
From www.chegg.com
Solved Obtain the transfer function Vout(s)/Vin(s) of the Transfer Function Vout/Vin In a simple circuit like the following: The laplace domain transfer function, if properly derived, is vout/vin where vout and vin are the laplace transforms of. H(s) = the transfer function of a circuit = transform of the output transform of the input. The systematic approach is not to use canned formulas at all, but derive the transfer function from. Transfer Function Vout/Vin.
From www.chegg.com
Solved 1. Plot the transfer function Vout vs. Vin for the Transfer Function Vout/Vin The transfer function h(s) of a circuit is defined as: In general, the transfer function \ ( h (s) \) of the cascaded circuit. (1) how do you derive this function? In a simple circuit like the following: I calculate the transfer function using i1 = i2: Vin = i1*r1 => i1 = vin / r1. H(s) = the transfer. Transfer Function Vout/Vin.
From www.chegg.com
Solved To be completed 1. Find the transfer function Transfer Function Vout/Vin (1) how do you derive this function? The transfer function h(s) of a circuit is defined as: The laplace domain transfer function, if properly derived, is vout/vin where vout and vin are the laplace transforms of. The systematic approach is not to use canned formulas at all, but derive the transfer function from first principles. I calculate the transfer function. Transfer Function Vout/Vin.
From www.chegg.com
Solved 3. Find the transfer function (Vout/Vin) of the Transfer Function Vout/Vin (1) how do you derive this function? In general, the transfer function \ ( h (s) \) of the cascaded circuit. The systematic approach is not to use canned formulas at all, but derive the transfer function from first principles. The laplace domain transfer function, if properly derived, is vout/vin where vout and vin are the laplace transforms of. H(s). Transfer Function Vout/Vin.
From www.numerade.com
SOLVED Question 01 Derive the transfer function (Vout/Vin) of the Transfer Function Vout/Vin I calculate the transfer function using i1 = i2: The systematic approach is not to use canned formulas at all, but derive the transfer function from first principles. The laplace domain transfer function, if properly derived, is vout/vin where vout and vin are the laplace transforms of. Transfer function of second order low pass filter. The transfer function h(s) of. Transfer Function Vout/Vin.
From www.coursehero.com
[Solved] Please find the transfer function (vout/vin) of this circuit Transfer Function Vout/Vin Transfer function of second order low pass filter. H(s) = the transfer function of a circuit = transform of the output transform of the input. The systematic approach is not to use canned formulas at all, but derive the transfer function from first principles. I calculate the transfer function using i1 = i2: (1) how do you derive this function?. Transfer Function Vout/Vin.
From www.chegg.com
Solved Using Kirchhoff's law the timedomain equations that Transfer Function Vout/Vin The laplace domain transfer function, if properly derived, is vout/vin where vout and vin are the laplace transforms of. Vin = i1*r1 => i1 = vin / r1. I calculate the transfer function using i1 = i2: (1) how do you derive this function? The transfer function h(s) of a circuit is defined as: In general, the transfer function \. Transfer Function Vout/Vin.
From www.chegg.com
Solved What is the transfer function (V out/Vin) for the Transfer Function Vout/Vin In a simple circuit like the following: The laplace domain transfer function, if properly derived, is vout/vin where vout and vin are the laplace transforms of. H(s) = the transfer function of a circuit = transform of the output transform of the input. The systematic approach is not to use canned formulas at all, but derive the transfer function from. Transfer Function Vout/Vin.
From www.chegg.com
The transfer function H(f)= Vout/Vin of a filter is Transfer Function Vout/Vin H(s) = the transfer function of a circuit = transform of the output transform of the input. I calculate the transfer function using i1 = i2: Vin = i1*r1 => i1 = vin / r1. (1) how do you derive this function? The systematic approach is not to use canned formulas at all, but derive the transfer function from first. Transfer Function Vout/Vin.
From www.chegg.com
Solved 8 Determine the transfer function Vout/Vin for the Transfer Function Vout/Vin (1) how do you derive this function? The transfer function h(s) of a circuit is defined as: Transfer function of second order low pass filter. In a simple circuit like the following: H(s) = the transfer function of a circuit = transform of the output transform of the input. I calculate the transfer function using i1 = i2: In general,. Transfer Function Vout/Vin.
From www.coursehero.com
[Solved] Please find the transfer function (vout/vin) of this circuit Transfer Function Vout/Vin In general, the transfer function \ ( h (s) \) of the cascaded circuit. I calculate the transfer function using i1 = i2: In a simple circuit like the following: Transfer function of second order low pass filter. (1) how do you derive this function? The laplace domain transfer function, if properly derived, is vout/vin where vout and vin are. Transfer Function Vout/Vin.
From www.chegg.com
Solved 4. (20 pts) Plot the transfer function (Vout/Vin) of Transfer Function Vout/Vin H(s) = the transfer function of a circuit = transform of the output transform of the input. I calculate the transfer function using i1 = i2: The laplace domain transfer function, if properly derived, is vout/vin where vout and vin are the laplace transforms of. In a simple circuit like the following: Vin = i1*r1 => i1 = vin /. Transfer Function Vout/Vin.
From www.chegg.com
Solved The transfer function H(f) = Vout/Vin of a filter is Transfer Function Vout/Vin I calculate the transfer function using i1 = i2: (1) how do you derive this function? The laplace domain transfer function, if properly derived, is vout/vin where vout and vin are the laplace transforms of. Vin = i1*r1 => i1 = vin / r1. In general, the transfer function \ ( h (s) \) of the cascaded circuit. H(s) =. Transfer Function Vout/Vin.
From www.chegg.com
Solved "Find the transfer function vout/vin" please show as Transfer Function Vout/Vin The laplace domain transfer function, if properly derived, is vout/vin where vout and vin are the laplace transforms of. In a simple circuit like the following: Vin = i1*r1 => i1 = vin / r1. H(s) = the transfer function of a circuit = transform of the output transform of the input. Transfer function of second order low pass filter.. Transfer Function Vout/Vin.
From www.coursehero.com
[Solved] Find the transfer function H(s) = Vout/Vin. 1. Find the Transfer Function Vout/Vin The transfer function h(s) of a circuit is defined as: The laplace domain transfer function, if properly derived, is vout/vin where vout and vin are the laplace transforms of. Vin = i1*r1 => i1 = vin / r1. I calculate the transfer function using i1 = i2: In general, the transfer function \ ( h (s) \) of the cascaded. Transfer Function Vout/Vin.
From www.numerade.com
VIDEO solution Example RL High Pass Filter Derive an expression for Transfer Function Vout/Vin In general, the transfer function \ ( h (s) \) of the cascaded circuit. The laplace domain transfer function, if properly derived, is vout/vin where vout and vin are the laplace transforms of. Vin = i1*r1 => i1 = vin / r1. Transfer function of second order low pass filter. I calculate the transfer function using i1 = i2: In. Transfer Function Vout/Vin.
From www.chegg.com
Solved Obtain the transfer function Vout(s)/Vin(s) of the Transfer Function Vout/Vin In general, the transfer function \ ( h (s) \) of the cascaded circuit. The transfer function h(s) of a circuit is defined as: Transfer function of second order low pass filter. Vin = i1*r1 => i1 = vin / r1. H(s) = the transfer function of a circuit = transform of the output transform of the input. The systematic. Transfer Function Vout/Vin.
From www.chegg.com
Solved Determine the transfer function Vout(s) / Vin(s) Transfer Function Vout/Vin I calculate the transfer function using i1 = i2: (1) how do you derive this function? The transfer function h(s) of a circuit is defined as: Transfer function of second order low pass filter. Vin = i1*r1 => i1 = vin / r1. In general, the transfer function \ ( h (s) \) of the cascaded circuit. In a simple. Transfer Function Vout/Vin.
From www.chegg.com
Solved 3. Plot the transfer function Vout vs. Vin for the Transfer Function Vout/Vin Vin = i1*r1 => i1 = vin / r1. The transfer function h(s) of a circuit is defined as: The laplace domain transfer function, if properly derived, is vout/vin where vout and vin are the laplace transforms of. In a simple circuit like the following: The systematic approach is not to use canned formulas at all, but derive the transfer. Transfer Function Vout/Vin.
From www.chegg.com
Solved 1. The Bode plot of a transfer function is given Transfer Function Vout/Vin Transfer function of second order low pass filter. In a simple circuit like the following: In general, the transfer function \ ( h (s) \) of the cascaded circuit. The laplace domain transfer function, if properly derived, is vout/vin where vout and vin are the laplace transforms of. H(s) = the transfer function of a circuit = transform of the. Transfer Function Vout/Vin.