Level Curve Equation . However, when the function has three. Recall that the level curves of a function f(x, y) f (x, y) are the curves given by f(x, y) = f (x, y) = constant. The level curves of the function \(z = f\left( {x,y} \right)\) are two dimensional curves we get by setting \(z = k\), where \(k\) is any. Given a function [latex]f\,(x,\ y)[/latex] and a number [latex]c[/latex] in the range of [latex]f[/latex], a level curve of a function of two variables for the value [latex]c[/latex] is defined. Sketch several traces or level curves of a function of two variables. A level set of a function of three variables $f(x,y,z)$ is a surface in three. Recognize a function of three or more variables and identify its. Level curves and contour plots.
from www.chegg.com
The level curves of the function \(z = f\left( {x,y} \right)\) are two dimensional curves we get by setting \(z = k\), where \(k\) is any. Sketch several traces or level curves of a function of two variables. However, when the function has three. Recall that the level curves of a function f(x, y) f (x, y) are the curves given by f(x, y) = f (x, y) = constant. Given a function [latex]f\,(x,\ y)[/latex] and a number [latex]c[/latex] in the range of [latex]f[/latex], a level curve of a function of two variables for the value [latex]c[/latex] is defined. A level set of a function of three variables $f(x,y,z)$ is a surface in three. Recognize a function of three or more variables and identify its. Level curves and contour plots.
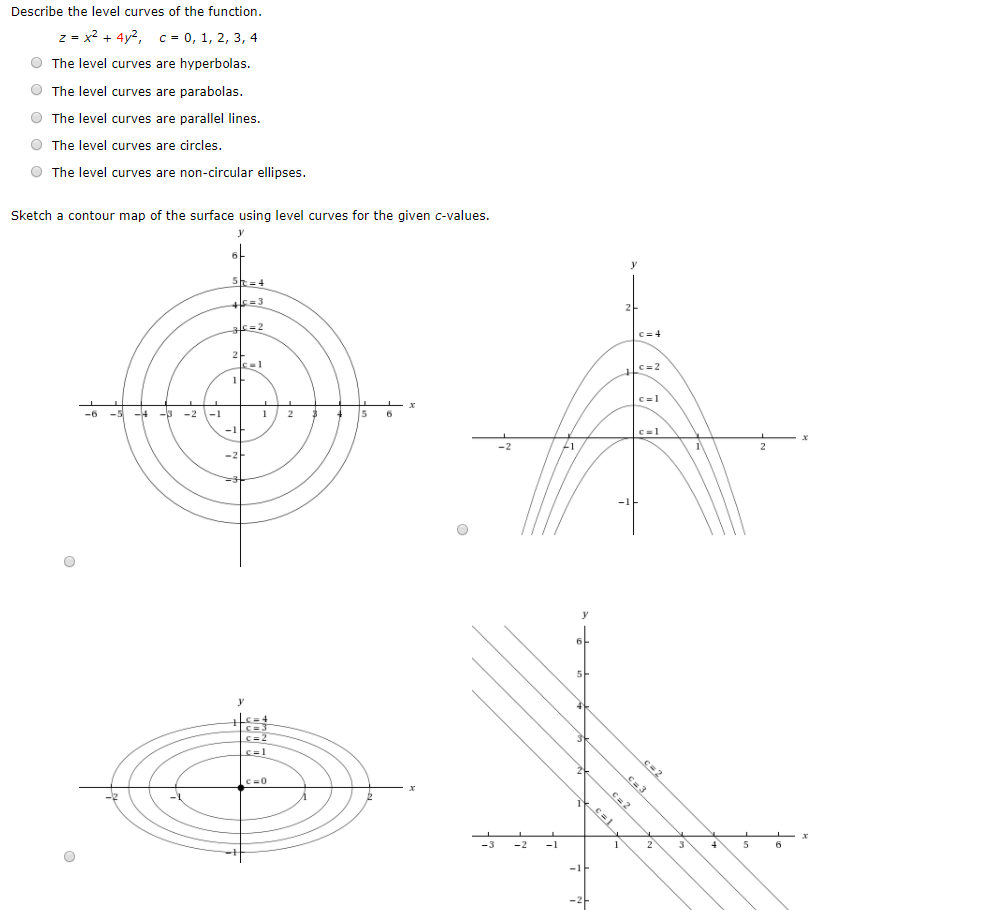
Solved Describe the level curves of the function. z=x2 +
Level Curve Equation Recall that the level curves of a function f(x, y) f (x, y) are the curves given by f(x, y) = f (x, y) = constant. Given a function [latex]f\,(x,\ y)[/latex] and a number [latex]c[/latex] in the range of [latex]f[/latex], a level curve of a function of two variables for the value [latex]c[/latex] is defined. The level curves of the function \(z = f\left( {x,y} \right)\) are two dimensional curves we get by setting \(z = k\), where \(k\) is any. Level curves and contour plots. Recall that the level curves of a function f(x, y) f (x, y) are the curves given by f(x, y) = f (x, y) = constant. Recognize a function of three or more variables and identify its. A level set of a function of three variables $f(x,y,z)$ is a surface in three. However, when the function has three. Sketch several traces or level curves of a function of two variables.
From www.youtube.com
Visualizing Surface and Level Curves YouTube Level Curve Equation Recognize a function of three or more variables and identify its. Sketch several traces or level curves of a function of two variables. Recall that the level curves of a function f(x, y) f (x, y) are the curves given by f(x, y) = f (x, y) = constant. Given a function [latex]f\,(x,\ y)[/latex] and a number [latex]c[/latex] in the. Level Curve Equation.
From www.chegg.com
Solved Describe the level curves of the function. z=x2 + Level Curve Equation Level curves and contour plots. Recognize a function of three or more variables and identify its. Recall that the level curves of a function f(x, y) f (x, y) are the curves given by f(x, y) = f (x, y) = constant. However, when the function has three. The level curves of the function \(z = f\left( {x,y} \right)\) are. Level Curve Equation.
From www.chegg.com
Solved 2 1 0 4552 Draw a contour map of the function Level Curve Equation Level curves and contour plots. However, when the function has three. Recognize a function of three or more variables and identify its. A level set of a function of three variables $f(x,y,z)$ is a surface in three. The level curves of the function \(z = f\left( {x,y} \right)\) are two dimensional curves we get by setting \(z = k\), where. Level Curve Equation.
From www.chegg.com
Solved (1 point) Each diagram represents the level curves of Level Curve Equation A level set of a function of three variables $f(x,y,z)$ is a surface in three. Recall that the level curves of a function f(x, y) f (x, y) are the curves given by f(x, y) = f (x, y) = constant. Recognize a function of three or more variables and identify its. The level curves of the function \(z =. Level Curve Equation.
From www.researchgate.net
Level curves of the function h w (x) with θ 0 = π/6 and w = 1/4. The... Download Scientific Level Curve Equation Recognize a function of three or more variables and identify its. The level curves of the function \(z = f\left( {x,y} \right)\) are two dimensional curves we get by setting \(z = k\), where \(k\) is any. Recall that the level curves of a function f(x, y) f (x, y) are the curves given by f(x, y) = f (x,. Level Curve Equation.
From www.dummies.com
Eight Basic Algebraic Curves dummies Level Curve Equation A level set of a function of three variables $f(x,y,z)$ is a surface in three. The level curves of the function \(z = f\left( {x,y} \right)\) are two dimensional curves we get by setting \(z = k\), where \(k\) is any. However, when the function has three. Given a function [latex]f\,(x,\ y)[/latex] and a number [latex]c[/latex] in the range of. Level Curve Equation.
From quizlet.com
Sketch the level curve z=k for the specified values of k. Quizlet Level Curve Equation Given a function [latex]f\,(x,\ y)[/latex] and a number [latex]c[/latex] in the range of [latex]f[/latex], a level curve of a function of two variables for the value [latex]c[/latex] is defined. Level curves and contour plots. A level set of a function of three variables $f(x,y,z)$ is a surface in three. Recall that the level curves of a function f(x, y) f. Level Curve Equation.
From www.youtube.com
Core 4 Maths ALevel Edexcel Parametric Equations (3) YouTube Level Curve Equation However, when the function has three. A level set of a function of three variables $f(x,y,z)$ is a surface in three. The level curves of the function \(z = f\left( {x,y} \right)\) are two dimensional curves we get by setting \(z = k\), where \(k\) is any. Recall that the level curves of a function f(x, y) f (x, y). Level Curve Equation.
From www.youtube.com
LO 100 Understand the relationship between the gradient and level curves of a two variable Level Curve Equation The level curves of the function \(z = f\left( {x,y} \right)\) are two dimensional curves we get by setting \(z = k\), where \(k\) is any. A level set of a function of three variables $f(x,y,z)$ is a surface in three. Level curves and contour plots. However, when the function has three. Recognize a function of three or more variables. Level Curve Equation.
From www.youtube.com
Curvas de nivel de funciones de dos variables YouTube Level Curve Equation A level set of a function of three variables $f(x,y,z)$ is a surface in three. Recognize a function of three or more variables and identify its. Level curves and contour plots. Given a function [latex]f\,(x,\ y)[/latex] and a number [latex]c[/latex] in the range of [latex]f[/latex], a level curve of a function of two variables for the value [latex]c[/latex] is defined.. Level Curve Equation.
From www.slideserve.com
PPT Lecture 5 Objective Equations PowerPoint Presentation, free download ID2797355 Level Curve Equation The level curves of the function \(z = f\left( {x,y} \right)\) are two dimensional curves we get by setting \(z = k\), where \(k\) is any. Sketch several traces or level curves of a function of two variables. Recognize a function of three or more variables and identify its. Given a function [latex]f\,(x,\ y)[/latex] and a number [latex]c[/latex] in the. Level Curve Equation.
From www.chegg.com
Solved Graph several level curves of the following function. Level Curve Equation Level curves and contour plots. Recognize a function of three or more variables and identify its. A level set of a function of three variables $f(x,y,z)$ is a surface in three. Given a function [latex]f\,(x,\ y)[/latex] and a number [latex]c[/latex] in the range of [latex]f[/latex], a level curve of a function of two variables for the value [latex]c[/latex] is defined.. Level Curve Equation.
From aleksandarhaber.com
Gentle Introduction to Gradients and Level Curves (Surfaces) Fusion of Engineering, Control Level Curve Equation A level set of a function of three variables $f(x,y,z)$ is a surface in three. However, when the function has three. Recall that the level curves of a function f(x, y) f (x, y) are the curves given by f(x, y) = f (x, y) = constant. Sketch several traces or level curves of a function of two variables. The. Level Curve Equation.
From www.chegg.com
Solved (5 points) Consider the surface in R 3 R3 given by z= Level Curve Equation A level set of a function of three variables $f(x,y,z)$ is a surface in three. Recall that the level curves of a function f(x, y) f (x, y) are the curves given by f(x, y) = f (x, y) = constant. The level curves of the function \(z = f\left( {x,y} \right)\) are two dimensional curves we get by setting. Level Curve Equation.
From www.youtube.com
Slope of a level curve YouTube Level Curve Equation A level set of a function of three variables $f(x,y,z)$ is a surface in three. Recognize a function of three or more variables and identify its. Level curves and contour plots. The level curves of the function \(z = f\left( {x,y} \right)\) are two dimensional curves we get by setting \(z = k\), where \(k\) is any. Recall that the. Level Curve Equation.
From studylib.net
2.9 Exact Equations and Level Curves Level Curve Equation A level set of a function of three variables $f(x,y,z)$ is a surface in three. Recall that the level curves of a function f(x, y) f (x, y) are the curves given by f(x, y) = f (x, y) = constant. However, when the function has three. Level curves and contour plots. The level curves of the function \(z =. Level Curve Equation.
From www.chegg.com
Solved Describe the level curves of the function. z=82x7y Level Curve Equation Recognize a function of three or more variables and identify its. Sketch several traces or level curves of a function of two variables. A level set of a function of three variables $f(x,y,z)$ is a surface in three. The level curves of the function \(z = f\left( {x,y} \right)\) are two dimensional curves we get by setting \(z = k\),. Level Curve Equation.
From corbettmaths.com
Equation of a Normal Revision Corbettmaths Level Curve Equation Recall that the level curves of a function f(x, y) f (x, y) are the curves given by f(x, y) = f (x, y) = constant. Given a function [latex]f\,(x,\ y)[/latex] and a number [latex]c[/latex] in the range of [latex]f[/latex], a level curve of a function of two variables for the value [latex]c[/latex] is defined. A level set of a. Level Curve Equation.
From www.youtube.com
Gradient and Tangents for Level Curves YouTube Level Curve Equation Sketch several traces or level curves of a function of two variables. However, when the function has three. A level set of a function of three variables $f(x,y,z)$ is a surface in three. Level curves and contour plots. Given a function [latex]f\,(x,\ y)[/latex] and a number [latex]c[/latex] in the range of [latex]f[/latex], a level curve of a function of two. Level Curve Equation.
From www.chegg.com
Solved Find the equation of the level curve of the function Level Curve Equation Recognize a function of three or more variables and identify its. Level curves and contour plots. A level set of a function of three variables $f(x,y,z)$ is a surface in three. Given a function [latex]f\,(x,\ y)[/latex] and a number [latex]c[/latex] in the range of [latex]f[/latex], a level curve of a function of two variables for the value [latex]c[/latex] is defined.. Level Curve Equation.
From www.pinterest.com
A level Maths P1 Topic Finding equation of a curve using Integration Math, Learning Level Curve Equation A level set of a function of three variables $f(x,y,z)$ is a surface in three. However, when the function has three. Level curves and contour plots. Sketch several traces or level curves of a function of two variables. The level curves of the function \(z = f\left( {x,y} \right)\) are two dimensional curves we get by setting \(z = k\),. Level Curve Equation.
From nextlevelmaths.com
Equations of Curves Poster Level Curve Equation Level curves and contour plots. A level set of a function of three variables $f(x,y,z)$ is a surface in three. The level curves of the function \(z = f\left( {x,y} \right)\) are two dimensional curves we get by setting \(z = k\), where \(k\) is any. Sketch several traces or level curves of a function of two variables. Recognize a. Level Curve Equation.
From www.chegg.com
Solved The Figure Shows Level Curves Of A Function F In T... Level Curve Equation Recognize a function of three or more variables and identify its. However, when the function has three. Recall that the level curves of a function f(x, y) f (x, y) are the curves given by f(x, y) = f (x, y) = constant. Sketch several traces or level curves of a function of two variables. Level curves and contour plots.. Level Curve Equation.
From www.coursehero.com
[Solved] equation in terms of x and y. Find an equation of the level curve... Course Hero Level Curve Equation However, when the function has three. Level curves and contour plots. Sketch several traces or level curves of a function of two variables. Recall that the level curves of a function f(x, y) f (x, y) are the curves given by f(x, y) = f (x, y) = constant. Recognize a function of three or more variables and identify its.. Level Curve Equation.
From www.youtube.com
Math 2110 Section 13.1 Level Curves and Level Surfaces YouTube Level Curve Equation However, when the function has three. Recall that the level curves of a function f(x, y) f (x, y) are the curves given by f(x, y) = f (x, y) = constant. Recognize a function of three or more variables and identify its. A level set of a function of three variables $f(x,y,z)$ is a surface in three. Given a. Level Curve Equation.
From www.youtube.com
How to find the equation of curve (Quadratic Chapter) YouTube Level Curve Equation A level set of a function of three variables $f(x,y,z)$ is a surface in three. Level curves and contour plots. However, when the function has three. Recognize a function of three or more variables and identify its. Recall that the level curves of a function f(x, y) f (x, y) are the curves given by f(x, y) = f (x,. Level Curve Equation.
From www.pinterest.com
How to Find the Level Curves of f(x, y) = cos((x^2 + 2y^2)/4) in 2020 Math videos, Math, Curves Level Curve Equation A level set of a function of three variables $f(x,y,z)$ is a surface in three. Recall that the level curves of a function f(x, y) f (x, y) are the curves given by f(x, y) = f (x, y) = constant. However, when the function has three. The level curves of the function \(z = f\left( {x,y} \right)\) are two. Level Curve Equation.
From bookdown.org
MATH1006 Calculus Level Curve Equation A level set of a function of three variables $f(x,y,z)$ is a surface in three. Recognize a function of three or more variables and identify its. Level curves and contour plots. However, when the function has three. Sketch several traces or level curves of a function of two variables. Given a function [latex]f\,(x,\ y)[/latex] and a number [latex]c[/latex] in the. Level Curve Equation.
From www.slideserve.com
PPT Lecture 5 Objective Equations PowerPoint Presentation, free download ID5463801 Level Curve Equation Recognize a function of three or more variables and identify its. The level curves of the function \(z = f\left( {x,y} \right)\) are two dimensional curves we get by setting \(z = k\), where \(k\) is any. A level set of a function of three variables $f(x,y,z)$ is a surface in three. Recall that the level curves of a function. Level Curve Equation.
From www.researchgate.net
The level curves defined by H ( ϕ , y ) = h . Download Scientific Diagram Level Curve Equation A level set of a function of three variables $f(x,y,z)$ is a surface in three. Given a function [latex]f\,(x,\ y)[/latex] and a number [latex]c[/latex] in the range of [latex]f[/latex], a level curve of a function of two variables for the value [latex]c[/latex] is defined. Level curves and contour plots. Recognize a function of three or more variables and identify its.. Level Curve Equation.
From www.numerade.com
SOLVEDDetermine the equation of the level curves f(x, y)=c and sketch the level curves for the Level Curve Equation Recognize a function of three or more variables and identify its. Given a function [latex]f\,(x,\ y)[/latex] and a number [latex]c[/latex] in the range of [latex]f[/latex], a level curve of a function of two variables for the value [latex]c[/latex] is defined. The level curves of the function \(z = f\left( {x,y} \right)\) are two dimensional curves we get by setting \(z. Level Curve Equation.
From www.numerade.com
SOLVEDDetermine the equation of the level curves f(x, y)=c and sketch the level curves for the Level Curve Equation Recognize a function of three or more variables and identify its. A level set of a function of three variables $f(x,y,z)$ is a surface in three. The level curves of the function \(z = f\left( {x,y} \right)\) are two dimensional curves we get by setting \(z = k\), where \(k\) is any. Recall that the level curves of a function. Level Curve Equation.
From www.youtube.com
Gradients and Level Curves YouTube Level Curve Equation However, when the function has three. Recognize a function of three or more variables and identify its. The level curves of the function \(z = f\left( {x,y} \right)\) are two dimensional curves we get by setting \(z = k\), where \(k\) is any. Recall that the level curves of a function f(x, y) f (x, y) are the curves given. Level Curve Equation.
From www.researchgate.net
Energy level curves associated with the conservative equation of (4),... Download Scientific Level Curve Equation A level set of a function of three variables $f(x,y,z)$ is a surface in three. However, when the function has three. Sketch several traces or level curves of a function of two variables. Recall that the level curves of a function f(x, y) f (x, y) are the curves given by f(x, y) = f (x, y) = constant. Given. Level Curve Equation.
From www.researchgate.net
Level curve of G( f, ˙ f ), see equation (8). Download Scientific Diagram Level Curve Equation Recognize a function of three or more variables and identify its. A level set of a function of three variables $f(x,y,z)$ is a surface in three. Level curves and contour plots. The level curves of the function \(z = f\left( {x,y} \right)\) are two dimensional curves we get by setting \(z = k\), where \(k\) is any. Given a function. Level Curve Equation.