Compact Difference Scheme . Compact differences for an ode • we had: U′′ n = un−1− 2un +un+1 h2 − 1 12 h2 f′′ −bu′′ +o(h4), (2) and therefore the original ode becomes, u′′ n. Learn how to approximate first and second derivatives using compact finite difference schemes on uniform meshes.
from www.semanticscholar.org
U′′ n = un−1− 2un +un+1 h2 − 1 12 h2 f′′ −bu′′ +o(h4), (2) and therefore the original ode becomes, u′′ n. Learn how to approximate first and second derivatives using compact finite difference schemes on uniform meshes. Compact differences for an ode • we had:
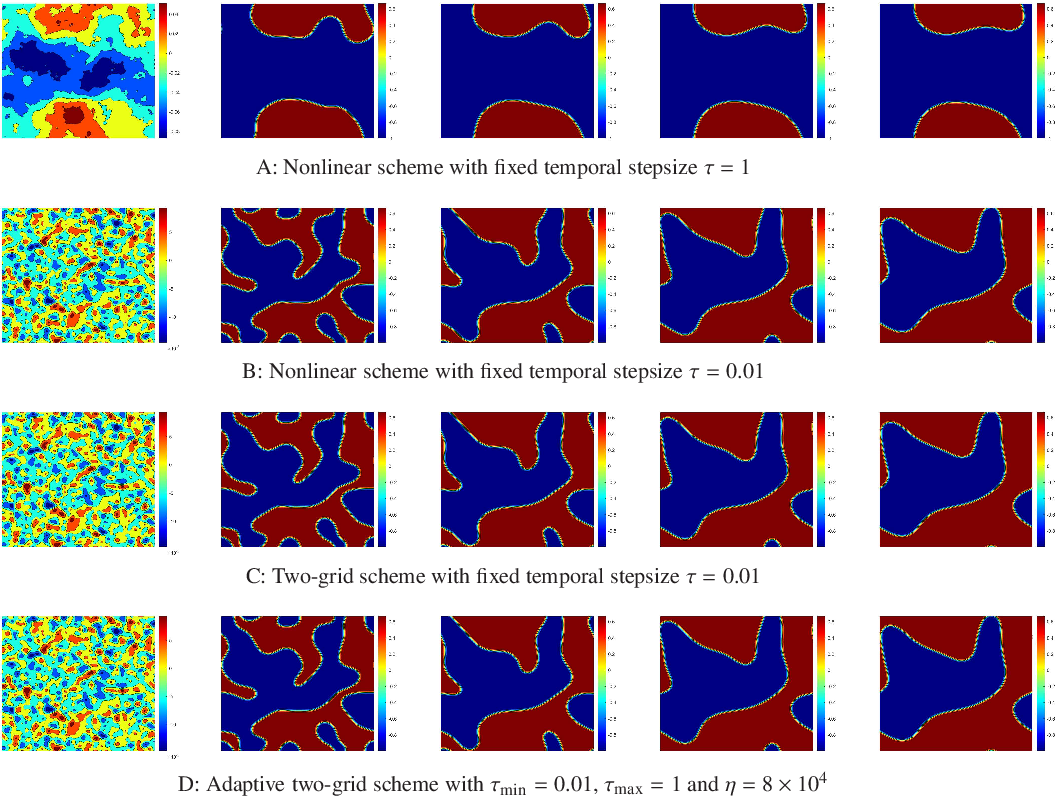
Figure 5 from An efficient twogrid fourthorder compact difference
Compact Difference Scheme Compact differences for an ode • we had: Learn how to approximate first and second derivatives using compact finite difference schemes on uniform meshes. Compact differences for an ode • we had: U′′ n = un−1− 2un +un+1 h2 − 1 12 h2 f′′ −bu′′ +o(h4), (2) and therefore the original ode becomes, u′′ n.
From www.researchgate.net
(PDF) A PredictorCorrector Compact Difference Scheme for a Compact Difference Scheme Learn how to approximate first and second derivatives using compact finite difference schemes on uniform meshes. Compact differences for an ode • we had: U′′ n = un−1− 2un +un+1 h2 − 1 12 h2 f′′ −bu′′ +o(h4), (2) and therefore the original ode becomes, u′′ n. Compact Difference Scheme.
From www.scientific.net
A FourthOrder Compact Finite Difference Scheme to the Numerical Compact Difference Scheme Compact differences for an ode • we had: Learn how to approximate first and second derivatives using compact finite difference schemes on uniform meshes. U′′ n = un−1− 2un +un+1 h2 − 1 12 h2 f′′ −bu′′ +o(h4), (2) and therefore the original ode becomes, u′′ n. Compact Difference Scheme.
From www.researchgate.net
(PDF) Discrete Maximum Principle and Energy Stability of the Compact Compact Difference Scheme Learn how to approximate first and second derivatives using compact finite difference schemes on uniform meshes. U′′ n = un−1− 2un +un+1 h2 − 1 12 h2 f′′ −bu′′ +o(h4), (2) and therefore the original ode becomes, u′′ n. Compact differences for an ode • we had: Compact Difference Scheme.
From www.researchgate.net
A proper orthogonal difference algorithm for Compact Difference Scheme Learn how to approximate first and second derivatives using compact finite difference schemes on uniform meshes. U′′ n = un−1− 2un +un+1 h2 − 1 12 h2 f′′ −bu′′ +o(h4), (2) and therefore the original ode becomes, u′′ n. Compact differences for an ode • we had: Compact Difference Scheme.
From deepai.org
A fast compact difference scheme with unequal timesteps for the Compact Difference Scheme U′′ n = un−1− 2un +un+1 h2 − 1 12 h2 f′′ −bu′′ +o(h4), (2) and therefore the original ode becomes, u′′ n. Compact differences for an ode • we had: Learn how to approximate first and second derivatives using compact finite difference schemes on uniform meshes. Compact Difference Scheme.
From dokumen.tips
(PDF) Fourthorder alternating direction implicit compact finite Compact Difference Scheme U′′ n = un−1− 2un +un+1 h2 − 1 12 h2 f′′ −bu′′ +o(h4), (2) and therefore the original ode becomes, u′′ n. Learn how to approximate first and second derivatives using compact finite difference schemes on uniform meshes. Compact differences for an ode • we had: Compact Difference Scheme.
From www.mdpi.com
Axioms Free FullText HigherOrder Blended Compact Difference Compact Difference Scheme Learn how to approximate first and second derivatives using compact finite difference schemes on uniform meshes. Compact differences for an ode • we had: U′′ n = un−1− 2un +un+1 h2 − 1 12 h2 f′′ −bu′′ +o(h4), (2) and therefore the original ode becomes, u′′ n. Compact Difference Scheme.
From www.mdpi.com
Axioms Free FullText HigherOrder Blended Compact Difference Compact Difference Scheme Compact differences for an ode • we had: Learn how to approximate first and second derivatives using compact finite difference schemes on uniform meshes. U′′ n = un−1− 2un +un+1 h2 − 1 12 h2 f′′ −bu′′ +o(h4), (2) and therefore the original ode becomes, u′′ n. Compact Difference Scheme.
From www.researchgate.net
(PDF) A 5th order monotonicitypreserving upwind compact difference scheme Compact Difference Scheme U′′ n = un−1− 2un +un+1 h2 − 1 12 h2 f′′ −bu′′ +o(h4), (2) and therefore the original ode becomes, u′′ n. Compact differences for an ode • we had: Learn how to approximate first and second derivatives using compact finite difference schemes on uniform meshes. Compact Difference Scheme.
From www.researchgate.net
Numerical analysis of an uncoupled and linearized compact difference Compact Difference Scheme U′′ n = un−1− 2un +un+1 h2 − 1 12 h2 f′′ −bu′′ +o(h4), (2) and therefore the original ode becomes, u′′ n. Learn how to approximate first and second derivatives using compact finite difference schemes on uniform meshes. Compact differences for an ode • we had: Compact Difference Scheme.
From www.researchgate.net
(PDF) AN EFFICIENT TWOGRID HIGHORDER COMPACT DIFFERENCE SCHEME WITH Compact Difference Scheme Compact differences for an ode • we had: Learn how to approximate first and second derivatives using compact finite difference schemes on uniform meshes. U′′ n = un−1− 2un +un+1 h2 − 1 12 h2 f′′ −bu′′ +o(h4), (2) and therefore the original ode becomes, u′′ n. Compact Difference Scheme.
From www.researchgate.net
(PDF) A Compact Difference Scheme for an Evolution Equation with a Compact Difference Scheme Compact differences for an ode • we had: U′′ n = un−1− 2un +un+1 h2 − 1 12 h2 f′′ −bu′′ +o(h4), (2) and therefore the original ode becomes, u′′ n. Learn how to approximate first and second derivatives using compact finite difference schemes on uniform meshes. Compact Difference Scheme.
From www.researchgate.net
When τ=0.3,0.5, the maximum of the scheme is (30). Download Compact Difference Scheme Compact differences for an ode • we had: U′′ n = un−1− 2un +un+1 h2 − 1 12 h2 f′′ −bu′′ +o(h4), (2) and therefore the original ode becomes, u′′ n. Learn how to approximate first and second derivatives using compact finite difference schemes on uniform meshes. Compact Difference Scheme.
From www.researchgate.net
(PDF) The CrankNicholson type compact difference scheme for a loaded Compact Difference Scheme U′′ n = un−1− 2un +un+1 h2 − 1 12 h2 f′′ −bu′′ +o(h4), (2) and therefore the original ode becomes, u′′ n. Learn how to approximate first and second derivatives using compact finite difference schemes on uniform meshes. Compact differences for an ode • we had: Compact Difference Scheme.
From www.researchgate.net
Conservative compact difference scheme based on the scalar auxiliary Compact Difference Scheme Compact differences for an ode • we had: Learn how to approximate first and second derivatives using compact finite difference schemes on uniform meshes. U′′ n = un−1− 2un +un+1 h2 − 1 12 h2 f′′ −bu′′ +o(h4), (2) and therefore the original ode becomes, u′′ n. Compact Difference Scheme.
From www.researchgate.net
(PDF) HigherOrder Blended Compact Difference Scheme on Nonuniform Compact Difference Scheme U′′ n = un−1− 2un +un+1 h2 − 1 12 h2 f′′ −bu′′ +o(h4), (2) and therefore the original ode becomes, u′′ n. Compact differences for an ode • we had: Learn how to approximate first and second derivatives using compact finite difference schemes on uniform meshes. Compact Difference Scheme.
From www.researchgate.net
(PDF) A Compact Difference Scheme for Fractional Subdiffusion Compact Difference Scheme Compact differences for an ode • we had: Learn how to approximate first and second derivatives using compact finite difference schemes on uniform meshes. U′′ n = un−1− 2un +un+1 h2 − 1 12 h2 f′′ −bu′′ +o(h4), (2) and therefore the original ode becomes, u′′ n. Compact Difference Scheme.
From www.researchgate.net
(PDF) Development of a fourthorder compact finite difference scheme Compact Difference Scheme U′′ n = un−1− 2un +un+1 h2 − 1 12 h2 f′′ −bu′′ +o(h4), (2) and therefore the original ode becomes, u′′ n. Learn how to approximate first and second derivatives using compact finite difference schemes on uniform meshes. Compact differences for an ode • we had: Compact Difference Scheme.
From www.academia.edu
(PDF) Fourth order compact difference scheme for 3D convection Compact Difference Scheme Learn how to approximate first and second derivatives using compact finite difference schemes on uniform meshes. U′′ n = un−1− 2un +un+1 h2 − 1 12 h2 f′′ −bu′′ +o(h4), (2) and therefore the original ode becomes, u′′ n. Compact differences for an ode • we had: Compact Difference Scheme.
From www.researchgate.net
(PDF) HighOrder Compact Difference Scheme and Multigrid Method for Compact Difference Scheme Learn how to approximate first and second derivatives using compact finite difference schemes on uniform meshes. U′′ n = un−1− 2un +un+1 h2 − 1 12 h2 f′′ −bu′′ +o(h4), (2) and therefore the original ode becomes, u′′ n. Compact differences for an ode • we had: Compact Difference Scheme.
From www.researchgate.net
(PDF) TimeSplitting Compact Difference Scheme for Solving Schrodinger Compact Difference Scheme Compact differences for an ode • we had: U′′ n = un−1− 2un +un+1 h2 − 1 12 h2 f′′ −bu′′ +o(h4), (2) and therefore the original ode becomes, u′′ n. Learn how to approximate first and second derivatives using compact finite difference schemes on uniform meshes. Compact Difference Scheme.
From www.tandfonline.com
Highorder compact difference scheme of 1D degenerate Compact Difference Scheme Compact differences for an ode • we had: U′′ n = un−1− 2un +un+1 h2 − 1 12 h2 f′′ −bu′′ +o(h4), (2) and therefore the original ode becomes, u′′ n. Learn how to approximate first and second derivatives using compact finite difference schemes on uniform meshes. Compact Difference Scheme.
From www.researchgate.net
Convergence order of compact difference scheme at T = 1 when τ = h² Compact Difference Scheme U′′ n = un−1− 2un +un+1 h2 − 1 12 h2 f′′ −bu′′ +o(h4), (2) and therefore the original ode becomes, u′′ n. Learn how to approximate first and second derivatives using compact finite difference schemes on uniform meshes. Compact differences for an ode • we had: Compact Difference Scheme.
From image.hanspub.org
求解薛定谔泊松方程组的时间分裂紧致差分格式 TimeSplitting Compact Difference Scheme for Compact Difference Scheme U′′ n = un−1− 2un +un+1 h2 − 1 12 h2 f′′ −bu′′ +o(h4), (2) and therefore the original ode becomes, u′′ n. Learn how to approximate first and second derivatives using compact finite difference schemes on uniform meshes. Compact differences for an ode • we had: Compact Difference Scheme.
From www.researchgate.net
(PDF) Sixth Order Compact Finite Difference Scheme for Steady State 1D Compact Difference Scheme Learn how to approximate first and second derivatives using compact finite difference schemes on uniform meshes. U′′ n = un−1− 2un +un+1 h2 − 1 12 h2 f′′ −bu′′ +o(h4), (2) and therefore the original ode becomes, u′′ n. Compact differences for an ode • we had: Compact Difference Scheme.
From www.researchgate.net
Numerical solution V of compact difference scheme at T = 1 with Compact Difference Scheme U′′ n = un−1− 2un +un+1 h2 − 1 12 h2 f′′ −bu′′ +o(h4), (2) and therefore the original ode becomes, u′′ n. Learn how to approximate first and second derivatives using compact finite difference schemes on uniform meshes. Compact differences for an ode • we had: Compact Difference Scheme.
From www.researchgate.net
The compact difference scheme for the fourth‐order nonlocal evolution Compact Difference Scheme U′′ n = un−1− 2un +un+1 h2 − 1 12 h2 f′′ −bu′′ +o(h4), (2) and therefore the original ode becomes, u′′ n. Compact differences for an ode • we had: Learn how to approximate first and second derivatives using compact finite difference schemes on uniform meshes. Compact Difference Scheme.
From www.mdpi.com
Mathematics Free FullText A HighOrder Compact (HOC) Implicit Compact Difference Scheme Learn how to approximate first and second derivatives using compact finite difference schemes on uniform meshes. U′′ n = un−1− 2un +un+1 h2 − 1 12 h2 f′′ −bu′′ +o(h4), (2) and therefore the original ode becomes, u′′ n. Compact differences for an ode • we had: Compact Difference Scheme.
From www.researchgate.net
The compact difference approach for the fourth‐order parabolic Compact Difference Scheme Learn how to approximate first and second derivatives using compact finite difference schemes on uniform meshes. Compact differences for an ode • we had: U′′ n = un−1− 2un +un+1 h2 − 1 12 h2 f′′ −bu′′ +o(h4), (2) and therefore the original ode becomes, u′′ n. Compact Difference Scheme.
From www.researchgate.net
(PDF) Efficiency of threepoint combined compact difference scheme Compact Difference Scheme U′′ n = un−1− 2un +un+1 h2 − 1 12 h2 f′′ −bu′′ +o(h4), (2) and therefore the original ode becomes, u′′ n. Compact differences for an ode • we had: Learn how to approximate first and second derivatives using compact finite difference schemes on uniform meshes. Compact Difference Scheme.
From www.researchgate.net
(PDF) Some aspects of compact difference scheme convergence Compact Difference Scheme Learn how to approximate first and second derivatives using compact finite difference schemes on uniform meshes. Compact differences for an ode • we had: U′′ n = un−1− 2un +un+1 h2 − 1 12 h2 f′′ −bu′′ +o(h4), (2) and therefore the original ode becomes, u′′ n. Compact Difference Scheme.
From www.semanticscholar.org
Figure 5 from An efficient twogrid fourthorder compact difference Compact Difference Scheme Compact differences for an ode • we had: Learn how to approximate first and second derivatives using compact finite difference schemes on uniform meshes. U′′ n = un−1− 2un +un+1 h2 − 1 12 h2 f′′ −bu′′ +o(h4), (2) and therefore the original ode becomes, u′′ n. Compact Difference Scheme.
From www.researchgate.net
(PDF) A fast compact difference scheme with unequal timesteps for the Compact Difference Scheme Compact differences for an ode • we had: Learn how to approximate first and second derivatives using compact finite difference schemes on uniform meshes. U′′ n = un−1− 2un +un+1 h2 − 1 12 h2 f′′ −bu′′ +o(h4), (2) and therefore the original ode becomes, u′′ n. Compact Difference Scheme.
From deepai.org
Pointwise error estimates of compact difference scheme for mixedtype Compact Difference Scheme Compact differences for an ode • we had: U′′ n = un−1− 2un +un+1 h2 − 1 12 h2 f′′ −bu′′ +o(h4), (2) and therefore the original ode becomes, u′′ n. Learn how to approximate first and second derivatives using compact finite difference schemes on uniform meshes. Compact Difference Scheme.
From www.researchgate.net
(PDF) A combined compact finite difference scheme for solving the Compact Difference Scheme Compact differences for an ode • we had: Learn how to approximate first and second derivatives using compact finite difference schemes on uniform meshes. U′′ n = un−1− 2un +un+1 h2 − 1 12 h2 f′′ −bu′′ +o(h4), (2) and therefore the original ode becomes, u′′ n. Compact Difference Scheme.