Does A Loop Count As An Edge . For example, in the following graph, a has degree 2, b has degree 6, d has degree 0, and so forth. $$\sum_{v \in v} \deg v = 2 \lvert e \rvert$$ this formula holds on loop. A loop is a multiset \(\{v,v\}=\{2\cdot v\}\) and multiple. A basic result of graph theory is the degree sum formula: Each edge has two ends, one end connects to one. In a simple graph, the degree of each vertex is equal to the number of incident edges. (for example from a a to itself). A graph \(g=(v,e)\) that is not simple can be represented by using multisets: The loop increases count by 2 2 because to assess degree, you just count how many wires are sticking out of the junction. A loop is commonly defined as an edge (or directed edge in the case of a digraph) with both ends as the same vertex.
from favtutor.com
A graph \(g=(v,e)\) that is not simple can be represented by using multisets: A loop is a multiset \(\{v,v\}=\{2\cdot v\}\) and multiple. The loop increases count by 2 2 because to assess degree, you just count how many wires are sticking out of the junction. In a simple graph, the degree of each vertex is equal to the number of incident edges. For example, in the following graph, a has degree 2, b has degree 6, d has degree 0, and so forth. Each edge has two ends, one end connects to one. $$\sum_{v \in v} \deg v = 2 \lvert e \rvert$$ this formula holds on loop. A loop is commonly defined as an edge (or directed edge in the case of a digraph) with both ends as the same vertex. (for example from a a to itself). A basic result of graph theory is the degree sum formula:
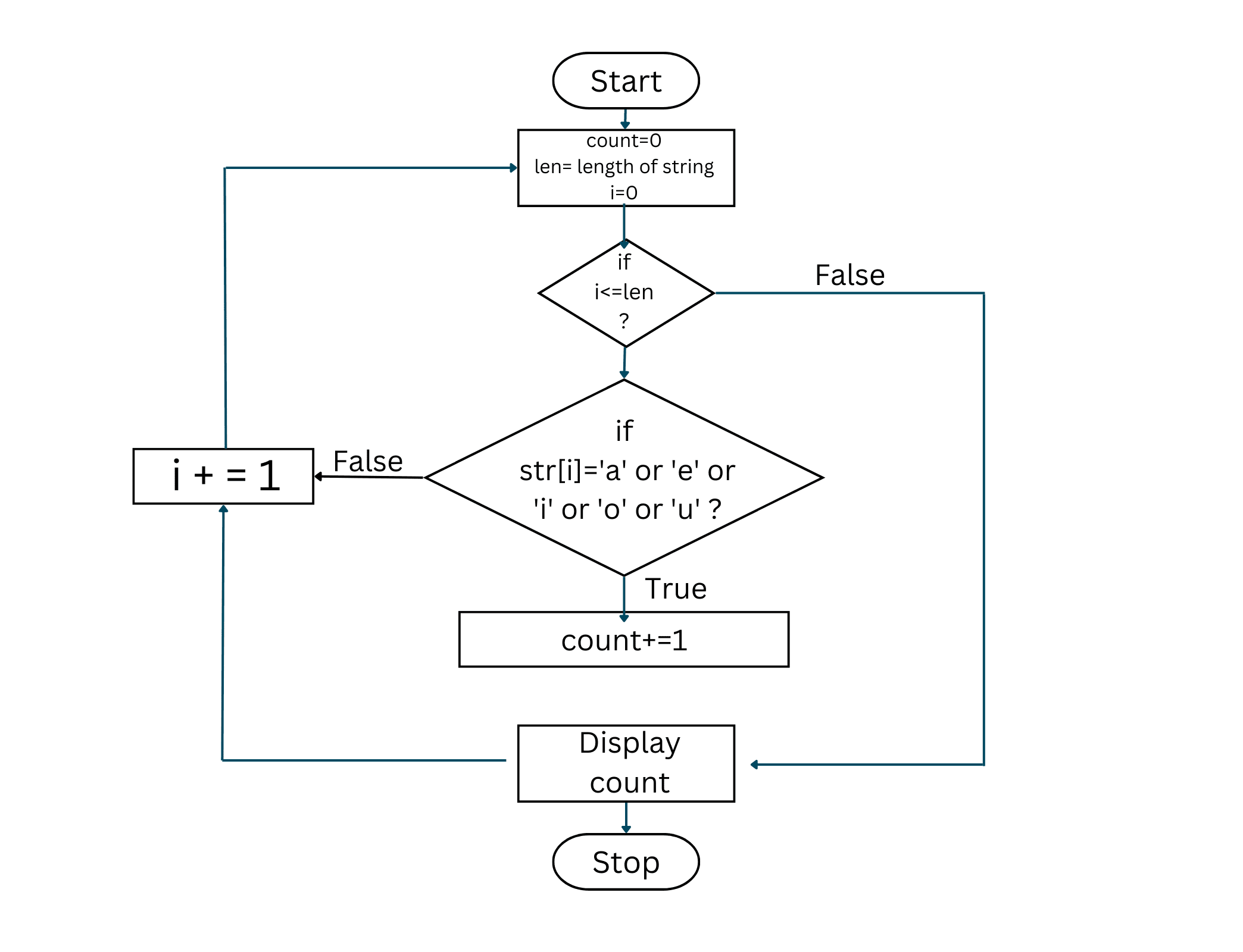
How to Count Vowels in a String using Python? (Loops & Lists)
Does A Loop Count As An Edge A loop is commonly defined as an edge (or directed edge in the case of a digraph) with both ends as the same vertex. A loop is commonly defined as an edge (or directed edge in the case of a digraph) with both ends as the same vertex. A graph \(g=(v,e)\) that is not simple can be represented by using multisets: A basic result of graph theory is the degree sum formula: A loop is a multiset \(\{v,v\}=\{2\cdot v\}\) and multiple. (for example from a a to itself). Each edge has two ends, one end connects to one. $$\sum_{v \in v} \deg v = 2 \lvert e \rvert$$ this formula holds on loop. In a simple graph, the degree of each vertex is equal to the number of incident edges. For example, in the following graph, a has degree 2, b has degree 6, d has degree 0, and so forth. The loop increases count by 2 2 because to assess degree, you just count how many wires are sticking out of the junction.
From www.youtube.com
How to connect loops with different edge counts [Blender tutorial part Does A Loop Count As An Edge $$\sum_{v \in v} \deg v = 2 \lvert e \rvert$$ this formula holds on loop. In a simple graph, the degree of each vertex is equal to the number of incident edges. Each edge has two ends, one end connects to one. The loop increases count by 2 2 because to assess degree, you just count how many wires are. Does A Loop Count As An Edge.
From www.toppr.com
The figure shows four wire loops, with edge lengths of either l or 2l Does A Loop Count As An Edge $$\sum_{v \in v} \deg v = 2 \lvert e \rvert$$ this formula holds on loop. For example, in the following graph, a has degree 2, b has degree 6, d has degree 0, and so forth. Each edge has two ends, one end connects to one. A loop is commonly defined as an edge (or directed edge in the case. Does A Loop Count As An Edge.
From www.slideserve.com
PPT 1) Fixed count loops 2) Variable count loops 3) Posttest Loops 4 Does A Loop Count As An Edge A graph \(g=(v,e)\) that is not simple can be represented by using multisets: Each edge has two ends, one end connects to one. A loop is a multiset \(\{v,v\}=\{2\cdot v\}\) and multiple. For example, in the following graph, a has degree 2, b has degree 6, d has degree 0, and so forth. The loop increases count by 2 2. Does A Loop Count As An Edge.
From www.slideserve.com
PPT 1) Fixed count loops 2) Variable count loops 3) Posttest Loops 4 Does A Loop Count As An Edge For example, in the following graph, a has degree 2, b has degree 6, d has degree 0, and so forth. A graph \(g=(v,e)\) that is not simple can be represented by using multisets: Each edge has two ends, one end connects to one. (for example from a a to itself). A basic result of graph theory is the degree. Does A Loop Count As An Edge.
From artisticrender.com
How to select an edge loop or face loop in Blender? Does A Loop Count As An Edge A loop is a multiset \(\{v,v\}=\{2\cdot v\}\) and multiple. $$\sum_{v \in v} \deg v = 2 \lvert e \rvert$$ this formula holds on loop. The loop increases count by 2 2 because to assess degree, you just count how many wires are sticking out of the junction. A loop is commonly defined as an edge (or directed edge in the. Does A Loop Count As An Edge.
From study.com
For Loop in C Programming Definition, Syntax & Examples Lesson Does A Loop Count As An Edge A basic result of graph theory is the degree sum formula: A graph \(g=(v,e)\) that is not simple can be represented by using multisets: A loop is a multiset \(\{v,v\}=\{2\cdot v\}\) and multiple. In a simple graph, the degree of each vertex is equal to the number of incident edges. $$\sum_{v \in v} \deg v = 2 \lvert e \rvert$$. Does A Loop Count As An Edge.
From www.slideserve.com
PPT Chapter 6 Looping PowerPoint Presentation, free download ID5897229 Does A Loop Count As An Edge A loop is commonly defined as an edge (or directed edge in the case of a digraph) with both ends as the same vertex. In a simple graph, the degree of each vertex is equal to the number of incident edges. Each edge has two ends, one end connects to one. A graph \(g=(v,e)\) that is not simple can be. Does A Loop Count As An Edge.
From www.slideserve.com
PPT Nested For Loops PowerPoint Presentation, free download ID1487323 Does A Loop Count As An Edge (for example from a a to itself). A graph \(g=(v,e)\) that is not simple can be represented by using multisets: For example, in the following graph, a has degree 2, b has degree 6, d has degree 0, and so forth. A basic result of graph theory is the degree sum formula: A loop is commonly defined as an edge. Does A Loop Count As An Edge.
From copyprogramming.com
Adding edge loops based on selected edges Does A Loop Count As An Edge The loop increases count by 2 2 because to assess degree, you just count how many wires are sticking out of the junction. In a simple graph, the degree of each vertex is equal to the number of incident edges. Each edge has two ends, one end connects to one. For example, in the following graph, a has degree 2,. Does A Loop Count As An Edge.
From www.youtube.com
Edge Loops for Beginners Blender Tutorial YouTube Does A Loop Count As An Edge A basic result of graph theory is the degree sum formula: A loop is a multiset \(\{v,v\}=\{2\cdot v\}\) and multiple. In a simple graph, the degree of each vertex is equal to the number of incident edges. A loop is commonly defined as an edge (or directed edge in the case of a digraph) with both ends as the same. Does A Loop Count As An Edge.
From css-tricks.com
Loop/count to provide visual clues CSSTricks CSSTricks Does A Loop Count As An Edge A basic result of graph theory is the degree sum formula: (for example from a a to itself). Each edge has two ends, one end connects to one. A graph \(g=(v,e)\) that is not simple can be represented by using multisets: A loop is a multiset \(\{v,v\}=\{2\cdot v\}\) and multiple. $$\sum_{v \in v} \deg v = 2 \lvert e \rvert$$. Does A Loop Count As An Edge.
From www.youtube.com
Worked example, for loop, count substring Iteration Computer Does A Loop Count As An Edge A loop is commonly defined as an edge (or directed edge in the case of a digraph) with both ends as the same vertex. Each edge has two ends, one end connects to one. $$\sum_{v \in v} \deg v = 2 \lvert e \rvert$$ this formula holds on loop. A basic result of graph theory is the degree sum formula:. Does A Loop Count As An Edge.
From www.chegg.com
Solved A conducting loop in the shape of a square of edge Does A Loop Count As An Edge Each edge has two ends, one end connects to one. A loop is commonly defined as an edge (or directed edge in the case of a digraph) with both ends as the same vertex. $$\sum_{v \in v} \deg v = 2 \lvert e \rvert$$ this formula holds on loop. (for example from a a to itself). A graph \(g=(v,e)\) that. Does A Loop Count As An Edge.
From artisticrender.com
How to select an edge loop or face loop in Blender? Does A Loop Count As An Edge For example, in the following graph, a has degree 2, b has degree 6, d has degree 0, and so forth. A graph \(g=(v,e)\) that is not simple can be represented by using multisets: A loop is commonly defined as an edge (or directed edge in the case of a digraph) with both ends as the same vertex. The loop. Does A Loop Count As An Edge.
From www.youtube.com
Nested Loops Explained (step by step) YouTube Does A Loop Count As An Edge (for example from a a to itself). A loop is commonly defined as an edge (or directed edge in the case of a digraph) with both ends as the same vertex. For example, in the following graph, a has degree 2, b has degree 6, d has degree 0, and so forth. A basic result of graph theory is the. Does A Loop Count As An Edge.
From www.youtube.com
Loops Part 5 While Loops CountControlled (Java) YouTube Does A Loop Count As An Edge A loop is a multiset \(\{v,v\}=\{2\cdot v\}\) and multiple. A loop is commonly defined as an edge (or directed edge in the case of a digraph) with both ends as the same vertex. A graph \(g=(v,e)\) that is not simple can be represented by using multisets: The loop increases count by 2 2 because to assess degree, you just count. Does A Loop Count As An Edge.
From www.slideserve.com
PPT 1) Fixed count loops 2) Variable count loops 3) Posttest Loops 4 Does A Loop Count As An Edge (for example from a a to itself). Each edge has two ends, one end connects to one. A graph \(g=(v,e)\) that is not simple can be represented by using multisets: In a simple graph, the degree of each vertex is equal to the number of incident edges. A loop is commonly defined as an edge (or directed edge in the. Does A Loop Count As An Edge.
From cgtyphoon.com
Redirection of the edge and polygon loops CGTyphoon Does A Loop Count As An Edge The loop increases count by 2 2 because to assess degree, you just count how many wires are sticking out of the junction. For example, in the following graph, a has degree 2, b has degree 6, d has degree 0, and so forth. A loop is a multiset \(\{v,v\}=\{2\cdot v\}\) and multiple. A graph \(g=(v,e)\) that is not simple. Does A Loop Count As An Edge.
From favtutor.com
How to Count Vowels in a String using Python? (Loops & Lists) Does A Loop Count As An Edge $$\sum_{v \in v} \deg v = 2 \lvert e \rvert$$ this formula holds on loop. The loop increases count by 2 2 because to assess degree, you just count how many wires are sticking out of the junction. A loop is commonly defined as an edge (or directed edge in the case of a digraph) with both ends as the. Does A Loop Count As An Edge.
From www.researchgate.net
Edge dislocation of an ZX loop, example of edge2 segment alongˆzalongˆ Does A Loop Count As An Edge For example, in the following graph, a has degree 2, b has degree 6, d has degree 0, and so forth. The loop increases count by 2 2 because to assess degree, you just count how many wires are sticking out of the junction. (for example from a a to itself). $$\sum_{v \in v} \deg v = 2 \lvert e. Does A Loop Count As An Edge.
From calcworkshop.com
Graph Theory (Defined w/ 5+ StepbyStep Examples!) Does A Loop Count As An Edge The loop increases count by 2 2 because to assess degree, you just count how many wires are sticking out of the junction. $$\sum_{v \in v} \deg v = 2 \lvert e \rvert$$ this formula holds on loop. (for example from a a to itself). A basic result of graph theory is the degree sum formula: A loop is a. Does A Loop Count As An Edge.
From www.scaler.com
Graph Data Structure Scaler Topics Does A Loop Count As An Edge $$\sum_{v \in v} \deg v = 2 \lvert e \rvert$$ this formula holds on loop. A loop is commonly defined as an edge (or directed edge in the case of a digraph) with both ends as the same vertex. For example, in the following graph, a has degree 2, b has degree 6, d has degree 0, and so forth.. Does A Loop Count As An Edge.
From www.freecodecamp.org
Python While Loop Tutorial While True Syntax Examples and Infinite Loops Does A Loop Count As An Edge A graph \(g=(v,e)\) that is not simple can be represented by using multisets: A basic result of graph theory is the degree sum formula: A loop is commonly defined as an edge (or directed edge in the case of a digraph) with both ends as the same vertex. For example, in the following graph, a has degree 2, b has. Does A Loop Count As An Edge.
From www.educba.com
JMeter Loop Count What is JMeter loop count? How to use? Does A Loop Count As An Edge A loop is a multiset \(\{v,v\}=\{2\cdot v\}\) and multiple. In a simple graph, the degree of each vertex is equal to the number of incident edges. Each edge has two ends, one end connects to one. $$\sum_{v \in v} \deg v = 2 \lvert e \rvert$$ this formula holds on loop. A basic result of graph theory is the degree. Does A Loop Count As An Edge.
From www.edrawmax.com
What Is Repetition in Flowcharts? A Few Examples to Understand this Does A Loop Count As An Edge A graph \(g=(v,e)\) that is not simple can be represented by using multisets: A loop is a multiset \(\{v,v\}=\{2\cdot v\}\) and multiple. In a simple graph, the degree of each vertex is equal to the number of incident edges. (for example from a a to itself). The loop increases count by 2 2 because to assess degree, you just count. Does A Loop Count As An Edge.
From www.chegg.com
Solved A circular edge dislocation loop is shown in Fig. Does A Loop Count As An Edge For example, in the following graph, a has degree 2, b has degree 6, d has degree 0, and so forth. (for example from a a to itself). $$\sum_{v \in v} \deg v = 2 \lvert e \rvert$$ this formula holds on loop. A basic result of graph theory is the degree sum formula: Each edge has two ends, one. Does A Loop Count As An Edge.
From www.slideserve.com
PPT for Loop Lesson 1 Outline PowerPoint Presentation, free download Does A Loop Count As An Edge In a simple graph, the degree of each vertex is equal to the number of incident edges. A loop is a multiset \(\{v,v\}=\{2\cdot v\}\) and multiple. Each edge has two ends, one end connects to one. A basic result of graph theory is the degree sum formula: A graph \(g=(v,e)\) that is not simple can be represented by using multisets:. Does A Loop Count As An Edge.
From www.slideserve.com
PPT for Loop Lesson 1 Outline PowerPoint Presentation, free download Does A Loop Count As An Edge For example, in the following graph, a has degree 2, b has degree 6, d has degree 0, and so forth. In a simple graph, the degree of each vertex is equal to the number of incident edges. A basic result of graph theory is the degree sum formula: A loop is a multiset \(\{v,v\}=\{2\cdot v\}\) and multiple. A loop. Does A Loop Count As An Edge.
From www.slideserve.com
PPT 1) Fixed count loops 2) Variable count loops 3) Posttest Loops 4 Does A Loop Count As An Edge A basic result of graph theory is the degree sum formula: A graph \(g=(v,e)\) that is not simple can be represented by using multisets: A loop is commonly defined as an edge (or directed edge in the case of a digraph) with both ends as the same vertex. (for example from a a to itself). Each edge has two ends,. Does A Loop Count As An Edge.
From www.slideserve.com
PPT 1) Fixed count loops 2) Variable count loops 3) Posttest Loops 4 Does A Loop Count As An Edge A loop is commonly defined as an edge (or directed edge in the case of a digraph) with both ends as the same vertex. For example, in the following graph, a has degree 2, b has degree 6, d has degree 0, and so forth. Each edge has two ends, one end connects to one. A basic result of graph. Does A Loop Count As An Edge.
From www.youtube.com
Looping structures in MATLAB Basic FOR loops YouTube Does A Loop Count As An Edge A loop is a multiset \(\{v,v\}=\{2\cdot v\}\) and multiple. A graph \(g=(v,e)\) that is not simple can be represented by using multisets: $$\sum_{v \in v} \deg v = 2 \lvert e \rvert$$ this formula holds on loop. A basic result of graph theory is the degree sum formula: In a simple graph, the degree of each vertex is equal to. Does A Loop Count As An Edge.
From www.researchgate.net
Counting loop example. Here the number of iterations of Line 12 depends Does A Loop Count As An Edge For example, in the following graph, a has degree 2, b has degree 6, d has degree 0, and so forth. A graph \(g=(v,e)\) that is not simple can be represented by using multisets: (for example from a a to itself). The loop increases count by 2 2 because to assess degree, you just count how many wires are sticking. Does A Loop Count As An Edge.
From www.youtube.com
Basic Graph Theory I vertices, edges, loops, and equivalent graphs Does A Loop Count As An Edge For example, in the following graph, a has degree 2, b has degree 6, d has degree 0, and so forth. A basic result of graph theory is the degree sum formula: A graph \(g=(v,e)\) that is not simple can be represented by using multisets: $$\sum_{v \in v} \deg v = 2 \lvert e \rvert$$ this formula holds on loop.. Does A Loop Count As An Edge.
From www.youtube.com
Moving Edge Loop (Geometry Nodes, Blender) YouTube Does A Loop Count As An Edge (for example from a a to itself). A loop is a multiset \(\{v,v\}=\{2\cdot v\}\) and multiple. A loop is commonly defined as an edge (or directed edge in the case of a digraph) with both ends as the same vertex. For example, in the following graph, a has degree 2, b has degree 6, d has degree 0, and so. Does A Loop Count As An Edge.
From www.slideserve.com
PPT H. Rosen Chapter 7 Graphs PowerPoint Presentation, free Does A Loop Count As An Edge A basic result of graph theory is the degree sum formula: A loop is a multiset \(\{v,v\}=\{2\cdot v\}\) and multiple. In a simple graph, the degree of each vertex is equal to the number of incident edges. $$\sum_{v \in v} \deg v = 2 \lvert e \rvert$$ this formula holds on loop. Each edge has two ends, one end connects. Does A Loop Count As An Edge.