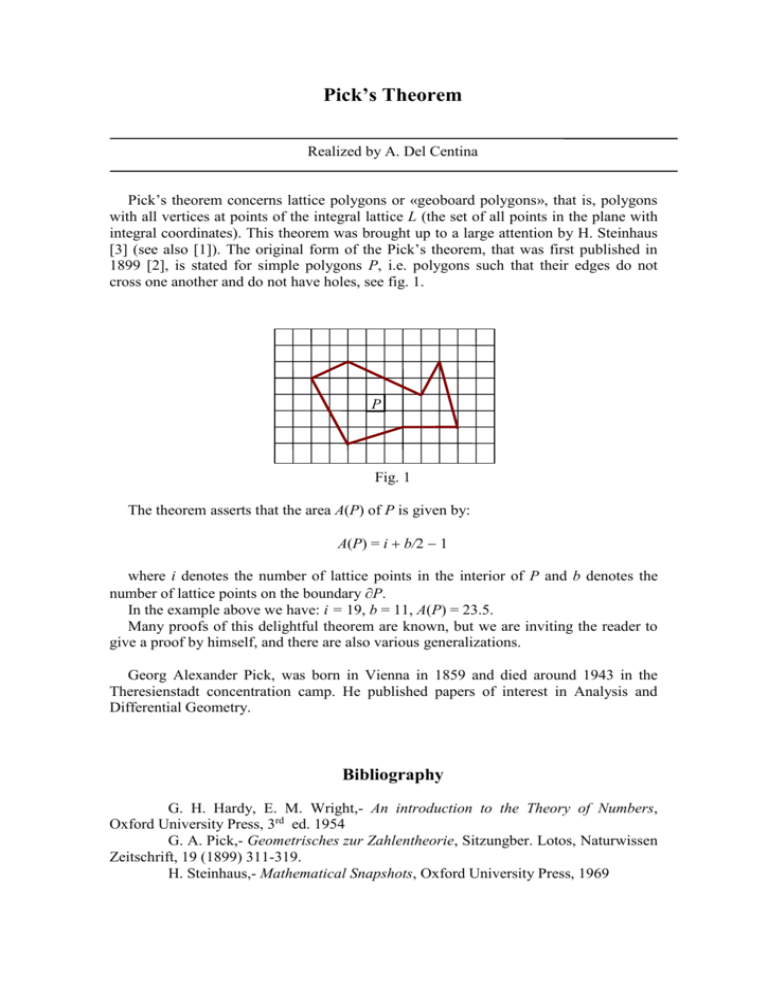
Pick's Theorem Problems . Find the area of a p olygon whose v ertices lie on unitary square grid. Pick's theorem let be the area of a simply closed lattice polygon. 2 7 6 4 1 3 5 a = 1 + 2 3 4 5 6 7 1. Lattice points are points whose. Pick's theorem gives a way to find the area of polygons in a plane whose endpoints have integer vertices. Let denote the number of lattice points on the polygon edges. Can you find the area of any polygon once you know the number of perimeter points and interior points? Click here for a poster of this problem. General case we now know that pick’s theorem is true for arbitrary triangles with their vertices on lattice points. Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms of the number of.
from studylib.net
Find the area of a p olygon whose v ertices lie on unitary square grid. Let denote the number of lattice points on the polygon edges. Lattice points are points whose. Click here for a poster of this problem. Pick's theorem gives a way to find the area of polygons in a plane whose endpoints have integer vertices. Can you find the area of any polygon once you know the number of perimeter points and interior points? 2 7 6 4 1 3 5 a = 1 + 2 3 4 5 6 7 1. Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms of the number of. Pick's theorem let be the area of a simply closed lattice polygon. General case we now know that pick’s theorem is true for arbitrary triangles with their vertices on lattice points.
Pick`s Theorem
Pick's Theorem Problems General case we now know that pick’s theorem is true for arbitrary triangles with their vertices on lattice points. General case we now know that pick’s theorem is true for arbitrary triangles with their vertices on lattice points. Can you find the area of any polygon once you know the number of perimeter points and interior points? 2 7 6 4 1 3 5 a = 1 + 2 3 4 5 6 7 1. Find the area of a p olygon whose v ertices lie on unitary square grid. Pick's theorem let be the area of a simply closed lattice polygon. Lattice points are points whose. Let denote the number of lattice points on the polygon edges. Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms of the number of. Pick's theorem gives a way to find the area of polygons in a plane whose endpoints have integer vertices. Click here for a poster of this problem.
From colleenyoung.org
Pick’s Theorem Mathematics, Learning and Technology Pick's Theorem Problems Click here for a poster of this problem. 2 7 6 4 1 3 5 a = 1 + 2 3 4 5 6 7 1. Pick's theorem let be the area of a simply closed lattice polygon. Find the area of a p olygon whose v ertices lie on unitary square grid. Let denote the number of lattice points. Pick's Theorem Problems.
From www.youtube.com
Pick's Theorem Area, boundary points, and interior points. YouTube Pick's Theorem Problems Can you find the area of any polygon once you know the number of perimeter points and interior points? Pick's theorem let be the area of a simply closed lattice polygon. Pick's theorem gives a way to find the area of polygons in a plane whose endpoints have integer vertices. General case we now know that pick’s theorem is true. Pick's Theorem Problems.
From quizlet.com
Pick's theoremA=\frac{1}{2} B+I1 Pick's theorem is an i Quizlet Pick's Theorem Problems Can you find the area of any polygon once you know the number of perimeter points and interior points? General case we now know that pick’s theorem is true for arbitrary triangles with their vertices on lattice points. Lattice points are points whose. Click here for a poster of this problem. Find the area of a p olygon whose v. Pick's Theorem Problems.
From www.youtube.com
Proving Pick's Theorem Infinite Series YouTube Pick's Theorem Problems Let denote the number of lattice points on the polygon edges. Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms of the number of. 2 7 6 4 1 3 5 a = 1 + 2 3 4 5 6 7 1. Pick's theorem let be the area. Pick's Theorem Problems.
From studylib.net
Pick`s Theorem Pick's Theorem Problems Can you find the area of any polygon once you know the number of perimeter points and interior points? Click here for a poster of this problem. General case we now know that pick’s theorem is true for arbitrary triangles with their vertices on lattice points. Lattice points are points whose. Pick's theorem expresses the area of a polygon, all. Pick's Theorem Problems.
From www.studypool.com
SOLUTION Pick's theorem (presentation) Studypool Pick's Theorem Problems General case we now know that pick’s theorem is true for arbitrary triangles with their vertices on lattice points. Pick's theorem let be the area of a simply closed lattice polygon. Pick's theorem gives a way to find the area of polygons in a plane whose endpoints have integer vertices. Pick's theorem expresses the area of a polygon, all of. Pick's Theorem Problems.
From fr.mathigon.org
Pick’s Theorem Mathigon Pick's Theorem Problems Pick's theorem let be the area of a simply closed lattice polygon. General case we now know that pick’s theorem is true for arbitrary triangles with their vertices on lattice points. Click here for a poster of this problem. Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms. Pick's Theorem Problems.
From yokehiang.blogspot.com
Yoke hiang & Math Pick's Theorem Problems Can you find the area of any polygon once you know the number of perimeter points and interior points? Lattice points are points whose. Find the area of a p olygon whose v ertices lie on unitary square grid. Pick's theorem let be the area of a simply closed lattice polygon. Let denote the number of lattice points on the. Pick's Theorem Problems.
From www.youtube.com
Pick's Theorem How to Work Out the Area of a Polygon Just by Counting Pick's Theorem Problems Pick's theorem gives a way to find the area of polygons in a plane whose endpoints have integer vertices. Can you find the area of any polygon once you know the number of perimeter points and interior points? Pick's theorem let be the area of a simply closed lattice polygon. Find the area of a p olygon whose v ertices. Pick's Theorem Problems.
From www.chegg.com
Solved Recall Pick's Theorem For The Area A Of A Lattice Pick's Theorem Problems 2 7 6 4 1 3 5 a = 1 + 2 3 4 5 6 7 1. Can you find the area of any polygon once you know the number of perimeter points and interior points? Click here for a poster of this problem. Pick's theorem let be the area of a simply closed lattice polygon. General case we. Pick's Theorem Problems.
From www.teachit.co.uk
Investigating area using Pick's theorem KS34 maths Teachit Pick's Theorem Problems Let denote the number of lattice points on the polygon edges. Can you find the area of any polygon once you know the number of perimeter points and interior points? Find the area of a p olygon whose v ertices lie on unitary square grid. 2 7 6 4 1 3 5 a = 1 + 2 3 4 5. Pick's Theorem Problems.
From www.youtube.com
Pick's Theorem YouTube Pick's Theorem Problems Lattice points are points whose. Let denote the number of lattice points on the polygon edges. Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms of the number of. Click here for a poster of this problem. General case we now know that pick’s theorem is true for. Pick's Theorem Problems.
From www.youtube.com
Pick's Theorem YouTube Pick's Theorem Problems Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms of the number of. Pick's theorem gives a way to find the area of polygons in a plane whose endpoints have integer vertices. Click here for a poster of this problem. Can you find the area of any polygon. Pick's Theorem Problems.
From colleenyoung.org
Pick’s Theorem Mathematics, Learning and Technology Pick's Theorem Problems Let denote the number of lattice points on the polygon edges. Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms of the number of. Click here for a poster of this problem. Can you find the area of any polygon once you know the number of perimeter points. Pick's Theorem Problems.
From hr.mathigon.org
Pick’s Theorem Mathigon Pick's Theorem Problems Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms of the number of. General case we now know that pick’s theorem is true for arbitrary triangles with their vertices on lattice points. 2 7 6 4 1 3 5 a = 1 + 2 3 4 5 6. Pick's Theorem Problems.
From www.youtube.com
Pick's Theorem YouTube Pick's Theorem Problems 2 7 6 4 1 3 5 a = 1 + 2 3 4 5 6 7 1. Can you find the area of any polygon once you know the number of perimeter points and interior points? General case we now know that pick’s theorem is true for arbitrary triangles with their vertices on lattice points. Lattice points are points. Pick's Theorem Problems.
From www.geogebra.org
Lesson Pick's Theorem GeoGebra Pick's Theorem Problems Let denote the number of lattice points on the polygon edges. Pick's theorem let be the area of a simply closed lattice polygon. Lattice points are points whose. Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms of the number of. General case we now know that pick’s. Pick's Theorem Problems.
From discover.hubpages.com
Pick’s Theorem To Find The Area Of A Polygon HubPages Pick's Theorem Problems Let denote the number of lattice points on the polygon edges. Find the area of a p olygon whose v ertices lie on unitary square grid. Pick's theorem let be the area of a simply closed lattice polygon. 2 7 6 4 1 3 5 a = 1 + 2 3 4 5 6 7 1. General case we now. Pick's Theorem Problems.
From www.scribd.com
A proof of Pick's theorem.pdf Triangle Polygon Pick's Theorem Problems Pick's theorem gives a way to find the area of polygons in a plane whose endpoints have integer vertices. Find the area of a p olygon whose v ertices lie on unitary square grid. 2 7 6 4 1 3 5 a = 1 + 2 3 4 5 6 7 1. General case we now know that pick’s theorem. Pick's Theorem Problems.
From blog.mrmeyer.com
Geometry Day 60 Pick’s Theorem & Treasure Hunt dy/dan Pick's Theorem Problems Lattice points are points whose. Pick's theorem let be the area of a simply closed lattice polygon. Can you find the area of any polygon once you know the number of perimeter points and interior points? General case we now know that pick’s theorem is true for arbitrary triangles with their vertices on lattice points. 2 7 6 4 1. Pick's Theorem Problems.
From www.youtube.com
Pick's Theorem (From Euler's Planar Graph Formula) YouTube Pick's Theorem Problems Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms of the number of. Find the area of a p olygon whose v ertices lie on unitary square grid. 2 7 6 4 1 3 5 a = 1 + 2 3 4 5 6 7 1. Pick's theorem. Pick's Theorem Problems.
From discover.hubpages.com
Pick’s Theorem To Find The Area Of A Polygon HubPages Pick's Theorem Problems Pick's theorem let be the area of a simply closed lattice polygon. Pick's theorem gives a way to find the area of polygons in a plane whose endpoints have integer vertices. Can you find the area of any polygon once you know the number of perimeter points and interior points? Lattice points are points whose. Let denote the number of. Pick's Theorem Problems.
From www.youtube.com
Lattice Points & Pick's Theorem IMO 1987 Problem 5 Cheenta YouTube Pick's Theorem Problems Pick's theorem gives a way to find the area of polygons in a plane whose endpoints have integer vertices. Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms of the number of. Click here for a poster of this problem. Lattice points are points whose. Pick's theorem let. Pick's Theorem Problems.
From www.studypool.com
SOLUTION Pick's theorem (presentation) Studypool Pick's Theorem Problems Pick's theorem gives a way to find the area of polygons in a plane whose endpoints have integer vertices. Click here for a poster of this problem. Let denote the number of lattice points on the polygon edges. Lattice points are points whose. Pick's theorem let be the area of a simply closed lattice polygon. Pick's theorem expresses the area. Pick's Theorem Problems.
From discover.hubpages.com
Pick’s Theorem To Find The Area Of A Polygon HubPages Pick's Theorem Problems Pick's theorem let be the area of a simply closed lattice polygon. Click here for a poster of this problem. General case we now know that pick’s theorem is true for arbitrary triangles with their vertices on lattice points. Lattice points are points whose. Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in. Pick's Theorem Problems.
From studylib.net
Pick’s Theorem Examples Tom Davis Part I Pick's Theorem Problems Let denote the number of lattice points on the polygon edges. Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms of the number of. General case we now know that pick’s theorem is true for arbitrary triangles with their vertices on lattice points. Click here for a poster. Pick's Theorem Problems.
From studylib.net
Pick`s Theorem Office for Mathematics, Science, and Technology Pick's Theorem Problems Let denote the number of lattice points on the polygon edges. 2 7 6 4 1 3 5 a = 1 + 2 3 4 5 6 7 1. Pick's theorem let be the area of a simply closed lattice polygon. General case we now know that pick’s theorem is true for arbitrary triangles with their vertices on lattice points.. Pick's Theorem Problems.
From www.studypool.com
SOLUTION Pick's theorem (presentation) Studypool Pick's Theorem Problems Pick's theorem let be the area of a simply closed lattice polygon. Lattice points are points whose. Can you find the area of any polygon once you know the number of perimeter points and interior points? General case we now know that pick’s theorem is true for arbitrary triangles with their vertices on lattice points. Find the area of a. Pick's Theorem Problems.
From www.scribd.com
Pick's Theorem PDF Pick's Theorem Problems General case we now know that pick’s theorem is true for arbitrary triangles with their vertices on lattice points. Pick's theorem gives a way to find the area of polygons in a plane whose endpoints have integer vertices. Can you find the area of any polygon once you know the number of perimeter points and interior points? Find the area. Pick's Theorem Problems.
From mathblogpro.blogspot.com
Math Blog Pro Blog 4 Pick's Theorem Pick's Theorem Problems Pick's theorem gives a way to find the area of polygons in a plane whose endpoints have integer vertices. Can you find the area of any polygon once you know the number of perimeter points and interior points? 2 7 6 4 1 3 5 a = 1 + 2 3 4 5 6 7 1. Let denote the number. Pick's Theorem Problems.
From connect.learnpad.com
Picks Theorem Content ClassConnect Pick's Theorem Problems General case we now know that pick’s theorem is true for arbitrary triangles with their vertices on lattice points. Pick's theorem gives a way to find the area of polygons in a plane whose endpoints have integer vertices. Find the area of a p olygon whose v ertices lie on unitary square grid. Click here for a poster of this. Pick's Theorem Problems.
From www.academia.edu
(PDF) A Colorful Proof of Pick’s Theorem Jack Graver Academia.edu Pick's Theorem Problems Pick's theorem let be the area of a simply closed lattice polygon. Let denote the number of lattice points on the polygon edges. 2 7 6 4 1 3 5 a = 1 + 2 3 4 5 6 7 1. Lattice points are points whose. Find the area of a p olygon whose v ertices lie on unitary square. Pick's Theorem Problems.
From discover.hubpages.com
Pick’s Theorem To Find The Area Of A Polygon HubPages Pick's Theorem Problems Find the area of a p olygon whose v ertices lie on unitary square grid. Lattice points are points whose. General case we now know that pick’s theorem is true for arbitrary triangles with their vertices on lattice points. Can you find the area of any polygon once you know the number of perimeter points and interior points? 2 7. Pick's Theorem Problems.
From www.studypool.com
SOLUTION Pick's theorem (presentation) Studypool Pick's Theorem Problems Lattice points are points whose. Find the area of a p olygon whose v ertices lie on unitary square grid. Let denote the number of lattice points on the polygon edges. Click here for a poster of this problem. Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms. Pick's Theorem Problems.
From hubpages.com
Pick’s Theorem To Find The Area Of A Polygon HubPages Pick's Theorem Problems 2 7 6 4 1 3 5 a = 1 + 2 3 4 5 6 7 1. Find the area of a p olygon whose v ertices lie on unitary square grid. Lattice points are points whose. Pick's theorem let be the area of a simply closed lattice polygon. Pick's theorem expresses the area of a polygon, all of. Pick's Theorem Problems.