Standard Basis In Linear Transformation . a linear transformation is a function \ (t\) from \ (\mathbb {r}^n\) to \ (\mathbb {r}^m\) that has the following properties. to see how important the choice of basis is, let’s use the standard basis for the linear transformation that projects the plane. In order to find this matrix, we must first define a special set of. to find the matrix representing a linear transformation in a given basis, apply the linear transformation to each. We define projection along a vector. In this subsection we will. if you manage to obtain the identity matrix on the left, then you know the images of the vectors from the standard basis, which is. how to find the matrix of a linear transformation. projections in rn is a good class of examples of linear transformations. find the matrix of a linear transformation with respect to the standard basis. Determine the action of a linear.
from www.chegg.com
a linear transformation is a function \ (t\) from \ (\mathbb {r}^n\) to \ (\mathbb {r}^m\) that has the following properties. We define projection along a vector. Determine the action of a linear. In this subsection we will. projections in rn is a good class of examples of linear transformations. if you manage to obtain the identity matrix on the left, then you know the images of the vectors from the standard basis, which is. In order to find this matrix, we must first define a special set of. how to find the matrix of a linear transformation. find the matrix of a linear transformation with respect to the standard basis. to find the matrix representing a linear transformation in a given basis, apply the linear transformation to each.
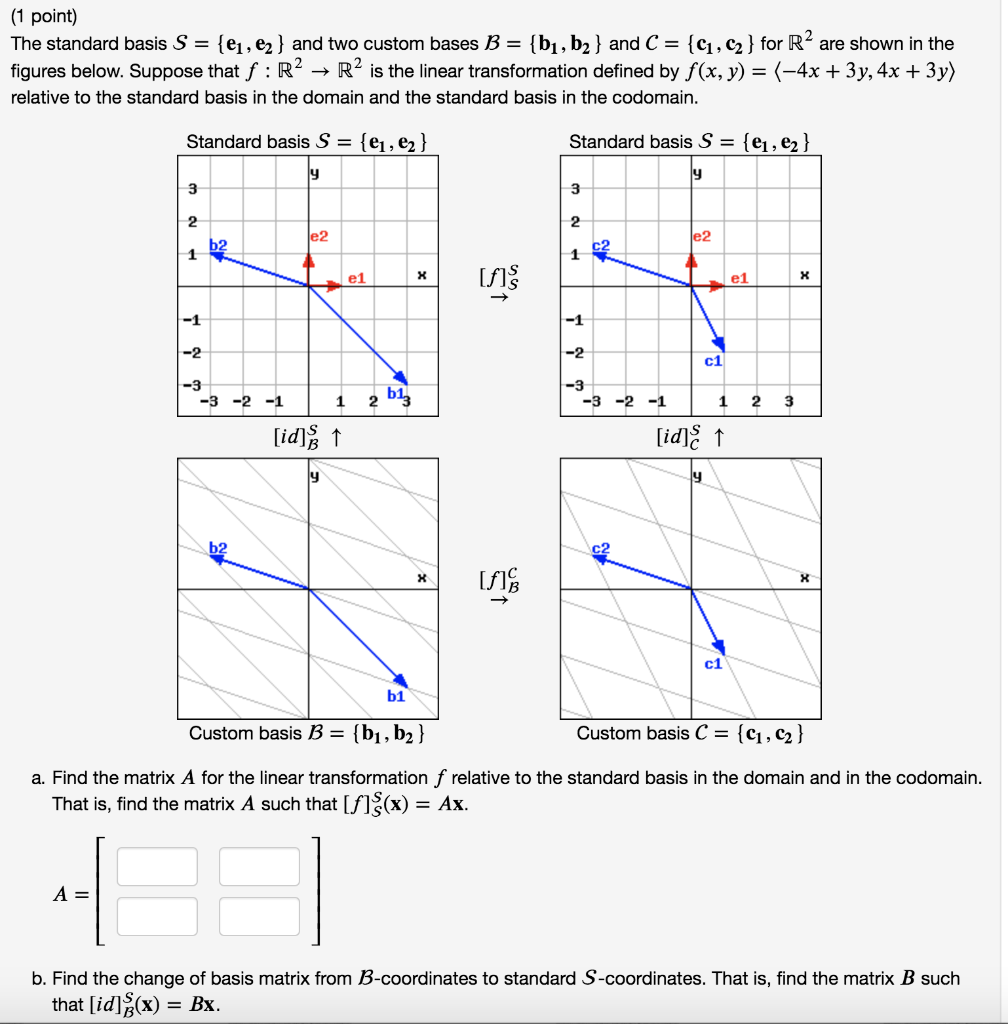
Solved (1 point) The standard basis S = {21, 22 } and two
Standard Basis In Linear Transformation how to find the matrix of a linear transformation. a linear transformation is a function \ (t\) from \ (\mathbb {r}^n\) to \ (\mathbb {r}^m\) that has the following properties. how to find the matrix of a linear transformation. find the matrix of a linear transformation with respect to the standard basis. In this subsection we will. projections in rn is a good class of examples of linear transformations. We define projection along a vector. to see how important the choice of basis is, let’s use the standard basis for the linear transformation that projects the plane. Determine the action of a linear. if you manage to obtain the identity matrix on the left, then you know the images of the vectors from the standard basis, which is. In order to find this matrix, we must first define a special set of. to find the matrix representing a linear transformation in a given basis, apply the linear transformation to each.
From www.chegg.com
Solved (1 point) The standard basis S = {21, 22 } and two Standard Basis In Linear Transformation Determine the action of a linear. find the matrix of a linear transformation with respect to the standard basis. how to find the matrix of a linear transformation. projections in rn is a good class of examples of linear transformations. In this subsection we will. We define projection along a vector. In order to find this matrix,. Standard Basis In Linear Transformation.
From www.chegg.com
Solved The standard basis S={e1,e2} and two custom bases Standard Basis In Linear Transformation to find the matrix representing a linear transformation in a given basis, apply the linear transformation to each. to see how important the choice of basis is, let’s use the standard basis for the linear transformation that projects the plane. We define projection along a vector. Determine the action of a linear. how to find the matrix. Standard Basis In Linear Transformation.
From www.chegg.com
Solved (1 point) The standard basis S = {eu, ez) and two Standard Basis In Linear Transformation We define projection along a vector. projections in rn is a good class of examples of linear transformations. to see how important the choice of basis is, let’s use the standard basis for the linear transformation that projects the plane. if you manage to obtain the identity matrix on the left, then you know the images of. Standard Basis In Linear Transformation.
From www.chegg.com
The standard basis S = (ei, e2} and two custom bases Standard Basis In Linear Transformation In order to find this matrix, we must first define a special set of. to see how important the choice of basis is, let’s use the standard basis for the linear transformation that projects the plane. Determine the action of a linear. if you manage to obtain the identity matrix on the left, then you know the images. Standard Basis In Linear Transformation.
From www.youtube.com
Find the Standard Matrix for the Composition of Two Linear Standard Basis In Linear Transformation In this subsection we will. how to find the matrix of a linear transformation. a linear transformation is a function \ (t\) from \ (\mathbb {r}^n\) to \ (\mathbb {r}^m\) that has the following properties. find the matrix of a linear transformation with respect to the standard basis. Determine the action of a linear. to see. Standard Basis In Linear Transformation.
From www.chegg.com
Solved Find the eigenvalues and eigenvectors of a linear Standard Basis In Linear Transformation In this subsection we will. In order to find this matrix, we must first define a special set of. if you manage to obtain the identity matrix on the left, then you know the images of the vectors from the standard basis, which is. projections in rn is a good class of examples of linear transformations. find. Standard Basis In Linear Transformation.
From www.youtube.com
Standard Matrix of a Linear Transformation YouTube Standard Basis In Linear Transformation We define projection along a vector. find the matrix of a linear transformation with respect to the standard basis. a linear transformation is a function \ (t\) from \ (\mathbb {r}^n\) to \ (\mathbb {r}^m\) that has the following properties. In order to find this matrix, we must first define a special set of. to see how. Standard Basis In Linear Transformation.
From www.youtube.com
How to Find the Matrix for a Linear Transformation Relative to Standard Standard Basis In Linear Transformation find the matrix of a linear transformation with respect to the standard basis. In this subsection we will. projections in rn is a good class of examples of linear transformations. to see how important the choice of basis is, let’s use the standard basis for the linear transformation that projects the plane. a linear transformation is. Standard Basis In Linear Transformation.
From www.chegg.com
Solved 7. The matrix A represents the linear transformation Standard Basis In Linear Transformation In this subsection we will. to see how important the choice of basis is, let’s use the standard basis for the linear transformation that projects the plane. how to find the matrix of a linear transformation. if you manage to obtain the identity matrix on the left, then you know the images of the vectors from the. Standard Basis In Linear Transformation.
From www.chegg.com
Solved The standard basis S={e1,e2} and two custom bases Standard Basis In Linear Transformation We define projection along a vector. find the matrix of a linear transformation with respect to the standard basis. to see how important the choice of basis is, let’s use the standard basis for the linear transformation that projects the plane. a linear transformation is a function \ (t\) from \ (\mathbb {r}^n\) to \ (\mathbb {r}^m\). Standard Basis In Linear Transformation.
From www.chegg.com
Solved (1 point) The standard basis E = {e1,e2 } and two Standard Basis In Linear Transformation In this subsection we will. to find the matrix representing a linear transformation in a given basis, apply the linear transformation to each. We define projection along a vector. find the matrix of a linear transformation with respect to the standard basis. projections in rn is a good class of examples of linear transformations. how to. Standard Basis In Linear Transformation.
From www.chegg.com
Solved (1 point) The standard basis E = {e1,e2 } and two Standard Basis In Linear Transformation In order to find this matrix, we must first define a special set of. if you manage to obtain the identity matrix on the left, then you know the images of the vectors from the standard basis, which is. to find the matrix representing a linear transformation in a given basis, apply the linear transformation to each. . Standard Basis In Linear Transformation.
From www.chegg.com
Solved Find the matrix A for each linear transformation T, Standard Basis In Linear Transformation to see how important the choice of basis is, let’s use the standard basis for the linear transformation that projects the plane. a linear transformation is a function \ (t\) from \ (\mathbb {r}^n\) to \ (\mathbb {r}^m\) that has the following properties. In this subsection we will. how to find the matrix of a linear transformation.. Standard Basis In Linear Transformation.
From www.chegg.com
Solved Consider the linear transformation T Rn → Rn whose Standard Basis In Linear Transformation if you manage to obtain the identity matrix on the left, then you know the images of the vectors from the standard basis, which is. Determine the action of a linear. how to find the matrix of a linear transformation. find the matrix of a linear transformation with respect to the standard basis. In order to find. Standard Basis In Linear Transformation.
From www.chegg.com
Solved The standard basis S = {ei, ez) and two custom bases Standard Basis In Linear Transformation if you manage to obtain the identity matrix on the left, then you know the images of the vectors from the standard basis, which is. Determine the action of a linear. how to find the matrix of a linear transformation. projections in rn is a good class of examples of linear transformations. to see how important. Standard Basis In Linear Transformation.
From www.studypug.com
Find the Standard Matrix of a Linear Transformation StudyPug Standard Basis In Linear Transformation In this subsection we will. how to find the matrix of a linear transformation. to see how important the choice of basis is, let’s use the standard basis for the linear transformation that projects the plane. We define projection along a vector. In order to find this matrix, we must first define a special set of. to. Standard Basis In Linear Transformation.
From www.youtube.com
Linear Transformations Find where T maps standard basis vector Standard Basis In Linear Transformation to see how important the choice of basis is, let’s use the standard basis for the linear transformation that projects the plane. Determine the action of a linear. We define projection along a vector. if you manage to obtain the identity matrix on the left, then you know the images of the vectors from the standard basis, which. Standard Basis In Linear Transformation.
From giorfikol.blob.core.windows.net
Standard Basis Linear Transformation at Ina Tran blog Standard Basis In Linear Transformation We define projection along a vector. to find the matrix representing a linear transformation in a given basis, apply the linear transformation to each. find the matrix of a linear transformation with respect to the standard basis. projections in rn is a good class of examples of linear transformations. to see how important the choice of. Standard Basis In Linear Transformation.
From math.stackexchange.com
Writing Linear Transformations as Matrices in Terms of the Standard Standard Basis In Linear Transformation a linear transformation is a function \ (t\) from \ (\mathbb {r}^n\) to \ (\mathbb {r}^m\) that has the following properties. We define projection along a vector. find the matrix of a linear transformation with respect to the standard basis. to see how important the choice of basis is, let’s use the standard basis for the linear. Standard Basis In Linear Transformation.
From www.youtube.com
Matrix Representation standard ordered Basis linear transformation T(5 Standard Basis In Linear Transformation to see how important the choice of basis is, let’s use the standard basis for the linear transformation that projects the plane. to find the matrix representing a linear transformation in a given basis, apply the linear transformation to each. if you manage to obtain the identity matrix on the left, then you know the images of. Standard Basis In Linear Transformation.
From www.chegg.com
Solved 1. Let T R3 R be a linear transformation. Let M (T) Standard Basis In Linear Transformation to find the matrix representing a linear transformation in a given basis, apply the linear transformation to each. how to find the matrix of a linear transformation. if you manage to obtain the identity matrix on the left, then you know the images of the vectors from the standard basis, which is. a linear transformation is. Standard Basis In Linear Transformation.
From giorfikol.blob.core.windows.net
Standard Basis Linear Transformation at Ina Tran blog Standard Basis In Linear Transformation if you manage to obtain the identity matrix on the left, then you know the images of the vectors from the standard basis, which is. to find the matrix representing a linear transformation in a given basis, apply the linear transformation to each. to see how important the choice of basis is, let’s use the standard basis. Standard Basis In Linear Transformation.
From www.chegg.com
Solved (1 pt) Find the matrix A of the linear transformation Standard Basis In Linear Transformation We define projection along a vector. a linear transformation is a function \ (t\) from \ (\mathbb {r}^n\) to \ (\mathbb {r}^m\) that has the following properties. to find the matrix representing a linear transformation in a given basis, apply the linear transformation to each. projections in rn is a good class of examples of linear transformations.. Standard Basis In Linear Transformation.
From www.chegg.com
Solved The standard basis S={e1,e2} and two custom bases Standard Basis In Linear Transformation In order to find this matrix, we must first define a special set of. to find the matrix representing a linear transformation in a given basis, apply the linear transformation to each. a linear transformation is a function \ (t\) from \ (\mathbb {r}^n\) to \ (\mathbb {r}^m\) that has the following properties. how to find the. Standard Basis In Linear Transformation.
From www.chegg.com
Solved The standard basis ={e1,e2} and two custom bases Standard Basis In Linear Transformation a linear transformation is a function \ (t\) from \ (\mathbb {r}^n\) to \ (\mathbb {r}^m\) that has the following properties. projections in rn is a good class of examples of linear transformations. In this subsection we will. We define projection along a vector. Determine the action of a linear. find the matrix of a linear transformation. Standard Basis In Linear Transformation.
From www.chegg.com
Solved The standard basis S={e1,e2} and two custom bases Standard Basis In Linear Transformation if you manage to obtain the identity matrix on the left, then you know the images of the vectors from the standard basis, which is. to see how important the choice of basis is, let’s use the standard basis for the linear transformation that projects the plane. We define projection along a vector. find the matrix of. Standard Basis In Linear Transformation.
From mbernste.github.io
Matrices characterize linear transformations Matthew N. Bernstein Standard Basis In Linear Transformation In order to find this matrix, we must first define a special set of. In this subsection we will. a linear transformation is a function \ (t\) from \ (\mathbb {r}^n\) to \ (\mathbb {r}^m\) that has the following properties. how to find the matrix of a linear transformation. to see how important the choice of basis. Standard Basis In Linear Transformation.
From www.chegg.com
Solved The standard basis S={e1,e2} and two custom bases Standard Basis In Linear Transformation We define projection along a vector. projections in rn is a good class of examples of linear transformations. to see how important the choice of basis is, let’s use the standard basis for the linear transformation that projects the plane. Determine the action of a linear. In this subsection we will. a linear transformation is a function. Standard Basis In Linear Transformation.
From www.studypug.com
Find the Standard Matrix of a Linear Transformation StudyPug Standard Basis In Linear Transformation In this subsection we will. Determine the action of a linear. a linear transformation is a function \ (t\) from \ (\mathbb {r}^n\) to \ (\mathbb {r}^m\) that has the following properties. if you manage to obtain the identity matrix on the left, then you know the images of the vectors from the standard basis, which is. . Standard Basis In Linear Transformation.
From www.chegg.com
Solved (1 point) The standard basis S {1,2} and two custom Standard Basis In Linear Transformation find the matrix of a linear transformation with respect to the standard basis. Determine the action of a linear. We define projection along a vector. In this subsection we will. how to find the matrix of a linear transformation. a linear transformation is a function \ (t\) from \ (\mathbb {r}^n\) to \ (\mathbb {r}^m\) that has. Standard Basis In Linear Transformation.
From mavink.com
Standard Matrix Of Linear Transformation Standard Basis In Linear Transformation if you manage to obtain the identity matrix on the left, then you know the images of the vectors from the standard basis, which is. In order to find this matrix, we must first define a special set of. We define projection along a vector. In this subsection we will. a linear transformation is a function \ (t\). Standard Basis In Linear Transformation.
From www.slideserve.com
PPT Chap. 6 Linear Transformations PowerPoint Presentation, free Standard Basis In Linear Transformation Determine the action of a linear. We define projection along a vector. if you manage to obtain the identity matrix on the left, then you know the images of the vectors from the standard basis, which is. find the matrix of a linear transformation with respect to the standard basis. In this subsection we will. a linear. Standard Basis In Linear Transformation.
From www.slideserve.com
PPT Chap. 6 Linear Transformations PowerPoint Presentation, free Standard Basis In Linear Transformation to see how important the choice of basis is, let’s use the standard basis for the linear transformation that projects the plane. projections in rn is a good class of examples of linear transformations. In order to find this matrix, we must first define a special set of. In this subsection we will. Determine the action of a. Standard Basis In Linear Transformation.
From www.youtube.com
Finding a Standard Matrix Using the Standard Basis YouTube Standard Basis In Linear Transformation Determine the action of a linear. In this subsection we will. a linear transformation is a function \ (t\) from \ (\mathbb {r}^n\) to \ (\mathbb {r}^m\) that has the following properties. projections in rn is a good class of examples of linear transformations. if you manage to obtain the identity matrix on the left, then you. Standard Basis In Linear Transformation.
From www.coursehero.com
[Solved] Find the standard matrix of the linear transformation Standard Basis In Linear Transformation if you manage to obtain the identity matrix on the left, then you know the images of the vectors from the standard basis, which is. to find the matrix representing a linear transformation in a given basis, apply the linear transformation to each. a linear transformation is a function \ (t\) from \ (\mathbb {r}^n\) to \. Standard Basis In Linear Transformation.