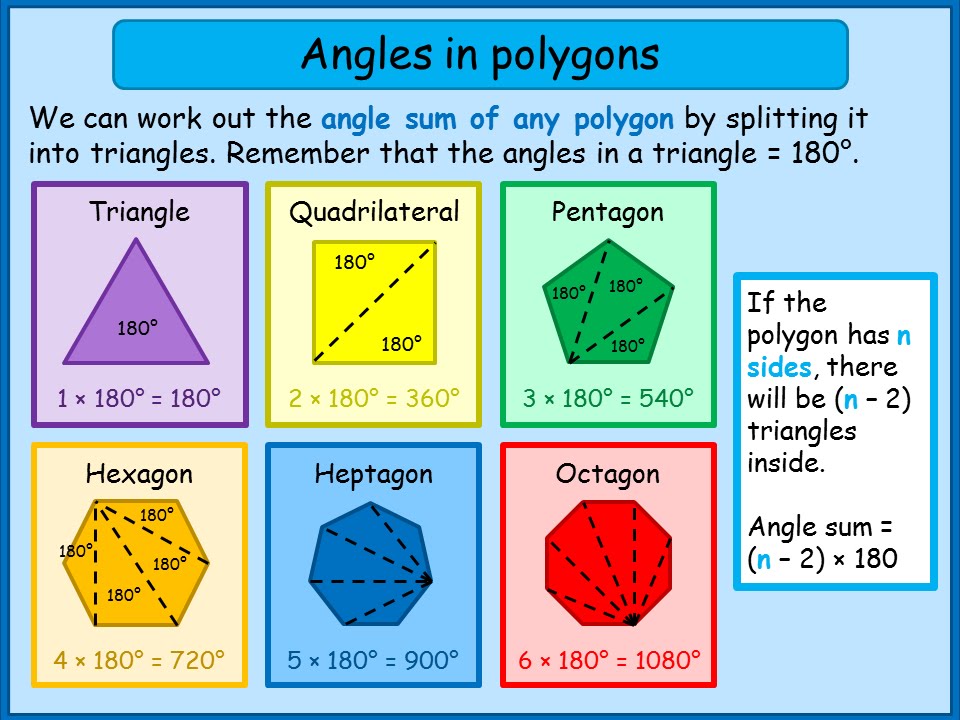
Number Of Triangles Formed In A Pentagon . The pattern developed in the example above, is consistent for all polygons. First, we count the number of triangles with all three vertices on the pentagon. The number of triangles formed by $ac$, $ad$ is $1+2=3$. Note that there are other formulas for the area of a triangle. Notice that any set of three points on the pentagon will form a triangle. The area for a triangle is a = ½ × base × height. In the adjoining figure of a pentagon abcde, on joining ac and ad, the given pentagon is. The triangles of a polygon are the triangles created by drawing line segments from one vertex of a polygon to all. The formula for the area of a rectangle is a = length × width. $bd$, $be$ form $6+11=17$ triangles. Using that, you get (n choose 3) as the number of possible triangles that can be formed by the vertices of a regular polygon of n sides. Triangles of a polygon definition: Consider a regular polygon with.
from www.youtube.com
The number of triangles formed by $ac$, $ad$ is $1+2=3$. Using that, you get (n choose 3) as the number of possible triangles that can be formed by the vertices of a regular polygon of n sides. Notice that any set of three points on the pentagon will form a triangle. Note that there are other formulas for the area of a triangle. The area for a triangle is a = ½ × base × height. In the adjoining figure of a pentagon abcde, on joining ac and ad, the given pentagon is. The pattern developed in the example above, is consistent for all polygons. First, we count the number of triangles with all three vertices on the pentagon. Triangles of a polygon definition: The formula for the area of a rectangle is a = length × width.
Angle sum of any polygon Maths Tutorials YouTube
Number Of Triangles Formed In A Pentagon Notice that any set of three points on the pentagon will form a triangle. First, we count the number of triangles with all three vertices on the pentagon. In the adjoining figure of a pentagon abcde, on joining ac and ad, the given pentagon is. Notice that any set of three points on the pentagon will form a triangle. The pattern developed in the example above, is consistent for all polygons. Consider a regular polygon with. Note that there are other formulas for the area of a triangle. The formula for the area of a rectangle is a = length × width. $bd$, $be$ form $6+11=17$ triangles. The number of triangles formed by $ac$, $ad$ is $1+2=3$. The area for a triangle is a = ½ × base × height. Triangles of a polygon definition: The triangles of a polygon are the triangles created by drawing line segments from one vertex of a polygon to all. Using that, you get (n choose 3) as the number of possible triangles that can be formed by the vertices of a regular polygon of n sides.
From www.youtube.com
how to find number of triangles in a given figure ssc cgl exam YouTube Number Of Triangles Formed In A Pentagon Consider a regular polygon with. The formula for the area of a rectangle is a = length × width. The pattern developed in the example above, is consistent for all polygons. $bd$, $be$ form $6+11=17$ triangles. The number of triangles formed by $ac$, $ad$ is $1+2=3$. Note that there are other formulas for the area of a triangle. First, we. Number Of Triangles Formed In A Pentagon.
From mathman.biz
Brenda's Pentagon Number Of Triangles Formed In A Pentagon The area for a triangle is a = ½ × base × height. The pattern developed in the example above, is consistent for all polygons. In the adjoining figure of a pentagon abcde, on joining ac and ad, the given pentagon is. Consider a regular polygon with. The number of triangles formed by $ac$, $ad$ is $1+2=3$. Note that there. Number Of Triangles Formed In A Pentagon.
From www.slideshare.net
A Triangle = A Pentagon Number Of Triangles Formed In A Pentagon The triangles of a polygon are the triangles created by drawing line segments from one vertex of a polygon to all. Note that there are other formulas for the area of a triangle. Using that, you get (n choose 3) as the number of possible triangles that can be formed by the vertices of a regular polygon of n sides.. Number Of Triangles Formed In A Pentagon.
From librewiki.net
램지의 정리 리브레 위키 Number Of Triangles Formed In A Pentagon Note that there are other formulas for the area of a triangle. The triangles of a polygon are the triangles created by drawing line segments from one vertex of a polygon to all. The area for a triangle is a = ½ × base × height. The pattern developed in the example above, is consistent for all polygons. The formula. Number Of Triangles Formed In A Pentagon.
From www.youtube.com
Triangle Counting Trick by Formula│Triangle Reasoning Shortcut Trick Type02 YouTube Number Of Triangles Formed In A Pentagon The area for a triangle is a = ½ × base × height. First, we count the number of triangles with all three vertices on the pentagon. $bd$, $be$ form $6+11=17$ triangles. The number of triangles formed by $ac$, $ad$ is $1+2=3$. Note that there are other formulas for the area of a triangle. Consider a regular polygon with. Notice. Number Of Triangles Formed In A Pentagon.
From undergroundmathematics.org
Solution Using angles in a pentagon... Trigonometry Compound Angles Underground Mathematics Number Of Triangles Formed In A Pentagon First, we count the number of triangles with all three vertices on the pentagon. The number of triangles formed by $ac$, $ad$ is $1+2=3$. Note that there are other formulas for the area of a triangle. $bd$, $be$ form $6+11=17$ triangles. The formula for the area of a rectangle is a = length × width. The triangles of a polygon. Number Of Triangles Formed In A Pentagon.
From www.researchgate.net
Matchsticks arranged as regular triangles, squares, pentagons and hexagons. Download Number Of Triangles Formed In A Pentagon Note that there are other formulas for the area of a triangle. The number of triangles formed by $ac$, $ad$ is $1+2=3$. $bd$, $be$ form $6+11=17$ triangles. The area for a triangle is a = ½ × base × height. Notice that any set of three points on the pentagon will form a triangle. Consider a regular polygon with. Using. Number Of Triangles Formed In A Pentagon.
From www.researchgate.net
(PDF) The Number of Triangles Formed by Intersecting Diagonals of a Regular Polygon Number Of Triangles Formed In A Pentagon Consider a regular polygon with. Using that, you get (n choose 3) as the number of possible triangles that can be formed by the vertices of a regular polygon of n sides. The number of triangles formed by $ac$, $ad$ is $1+2=3$. $bd$, $be$ form $6+11=17$ triangles. The pattern developed in the example above, is consistent for all polygons. Note. Number Of Triangles Formed In A Pentagon.
From cededre.com
Pentagon Shape Definition, Properties, Formulas, Examples (2022) Number Of Triangles Formed In A Pentagon First, we count the number of triangles with all three vertices on the pentagon. Notice that any set of three points on the pentagon will form a triangle. The pattern developed in the example above, is consistent for all polygons. The formula for the area of a rectangle is a = length × width. In the adjoining figure of a. Number Of Triangles Formed In A Pentagon.
From www.youtube.com
Angle sum of any polygon Maths Tutorials YouTube Number Of Triangles Formed In A Pentagon Notice that any set of three points on the pentagon will form a triangle. The triangles of a polygon are the triangles created by drawing line segments from one vertex of a polygon to all. The number of triangles formed by $ac$, $ad$ is $1+2=3$. Consider a regular polygon with. First, we count the number of triangles with all three. Number Of Triangles Formed In A Pentagon.
From www.mathswithmum.com
Angles in a Pentagon Maths with Mum Number Of Triangles Formed In A Pentagon The pattern developed in the example above, is consistent for all polygons. In the adjoining figure of a pentagon abcde, on joining ac and ad, the given pentagon is. The formula for the area of a rectangle is a = length × width. The triangles of a polygon are the triangles created by drawing line segments from one vertex of. Number Of Triangles Formed In A Pentagon.
From www.vedantu.com
A pentagon can be divided into how many triangles by drawing all of the diagonals from one vertex? Number Of Triangles Formed In A Pentagon The number of triangles formed by $ac$, $ad$ is $1+2=3$. Using that, you get (n choose 3) as the number of possible triangles that can be formed by the vertices of a regular polygon of n sides. The area for a triangle is a = ½ × base × height. Consider a regular polygon with. First, we count the number. Number Of Triangles Formed In A Pentagon.
From mungfali.com
How Many Triangles Can A Pentagon Make Number Of Triangles Formed In A Pentagon The pattern developed in the example above, is consistent for all polygons. Notice that any set of three points on the pentagon will form a triangle. In the adjoining figure of a pentagon abcde, on joining ac and ad, the given pentagon is. First, we count the number of triangles with all three vertices on the pentagon. Consider a regular. Number Of Triangles Formed In A Pentagon.
From www.researchgate.net
Diagram of pentagon with triangles. Diagram of pentagon with triangles. Download Scientific Number Of Triangles Formed In A Pentagon Using that, you get (n choose 3) as the number of possible triangles that can be formed by the vertices of a regular polygon of n sides. Note that there are other formulas for the area of a triangle. The pattern developed in the example above, is consistent for all polygons. Notice that any set of three points on the. Number Of Triangles Formed In A Pentagon.
From www.amathsdictionaryforkids.com
pentagonal numbers A Maths Dictionary for Kids Quick Reference by Jenny Eather Number Of Triangles Formed In A Pentagon The area for a triangle is a = ½ × base × height. Consider a regular polygon with. Using that, you get (n choose 3) as the number of possible triangles that can be formed by the vertices of a regular polygon of n sides. Note that there are other formulas for the area of a triangle. The formula for. Number Of Triangles Formed In A Pentagon.
From thirdspacelearning.com
Angles In A Pentagon GCSE Maths Steps & Examples Number Of Triangles Formed In A Pentagon First, we count the number of triangles with all three vertices on the pentagon. $bd$, $be$ form $6+11=17$ triangles. The number of triangles formed by $ac$, $ad$ is $1+2=3$. The pattern developed in the example above, is consistent for all polygons. In the adjoining figure of a pentagon abcde, on joining ac and ad, the given pentagon is. Triangles of. Number Of Triangles Formed In A Pentagon.
From mathblog.com
The Pentagon Shape Types, Formulas and Fun Facts Number Of Triangles Formed In A Pentagon Note that there are other formulas for the area of a triangle. Consider a regular polygon with. The formula for the area of a rectangle is a = length × width. $bd$, $be$ form $6+11=17$ triangles. The number of triangles formed by $ac$, $ad$ is $1+2=3$. The pattern developed in the example above, is consistent for all polygons. In the. Number Of Triangles Formed In A Pentagon.
From www.vedantu.com
A pentagon can be divided into how many triangles by drawing all of the diagonals from one vertex? Number Of Triangles Formed In A Pentagon Using that, you get (n choose 3) as the number of possible triangles that can be formed by the vertices of a regular polygon of n sides. The triangles of a polygon are the triangles created by drawing line segments from one vertex of a polygon to all. Note that there are other formulas for the area of a triangle.. Number Of Triangles Formed In A Pentagon.
From donsteward.blogspot.com
MEDIAN Don Steward mathematics teaching pentagon angles Number Of Triangles Formed In A Pentagon Triangles of a polygon definition: Note that there are other formulas for the area of a triangle. The triangles of a polygon are the triangles created by drawing line segments from one vertex of a polygon to all. Consider a regular polygon with. First, we count the number of triangles with all three vertices on the pentagon. In the adjoining. Number Of Triangles Formed In A Pentagon.
From byjus.com
Pentagon Definition, Shape, Properties, Types, Formula & Example Number Of Triangles Formed In A Pentagon Triangles of a polygon definition: The number of triangles formed by $ac$, $ad$ is $1+2=3$. First, we count the number of triangles with all three vertices on the pentagon. $bd$, $be$ form $6+11=17$ triangles. The triangles of a polygon are the triangles created by drawing line segments from one vertex of a polygon to all. Note that there are other. Number Of Triangles Formed In A Pentagon.
From byjus.com
Polygon Types, Classification & Formulas, Triangles, Quadrilateral, 3D Shapes Number Of Triangles Formed In A Pentagon $bd$, $be$ form $6+11=17$ triangles. The number of triangles formed by $ac$, $ad$ is $1+2=3$. Note that there are other formulas for the area of a triangle. The triangles of a polygon are the triangles created by drawing line segments from one vertex of a polygon to all. The area for a triangle is a = ½ × base ×. Number Of Triangles Formed In A Pentagon.
From brainly.ph
Did you see a pattern on the number of triangles formed with respect to the number of sides of Number Of Triangles Formed In A Pentagon The formula for the area of a rectangle is a = length × width. Note that there are other formulas for the area of a triangle. Using that, you get (n choose 3) as the number of possible triangles that can be formed by the vertices of a regular polygon of n sides. The pattern developed in the example above,. Number Of Triangles Formed In A Pentagon.
From www.cosmic-core.org
Article 32 Number The Triad Part 6 Triangles, Polygons, & Platonic Solids Cosmic Core Number Of Triangles Formed In A Pentagon Triangles of a polygon definition: The area for a triangle is a = ½ × base × height. First, we count the number of triangles with all three vertices on the pentagon. Using that, you get (n choose 3) as the number of possible triangles that can be formed by the vertices of a regular polygon of n sides. The. Number Of Triangles Formed In A Pentagon.
From www.pinterest.at
a table with numbers and shapes for regular polygons fact chart, which shows the number of Number Of Triangles Formed In A Pentagon The formula for the area of a rectangle is a = length × width. $bd$, $be$ form $6+11=17$ triangles. Note that there are other formulas for the area of a triangle. Using that, you get (n choose 3) as the number of possible triangles that can be formed by the vertices of a regular polygon of n sides. First, we. Number Of Triangles Formed In A Pentagon.
From pt.slideshare.net
Chapter 3 Figurate Numbers Number Of Triangles Formed In A Pentagon The number of triangles formed by $ac$, $ad$ is $1+2=3$. First, we count the number of triangles with all three vertices on the pentagon. Using that, you get (n choose 3) as the number of possible triangles that can be formed by the vertices of a regular polygon of n sides. The area for a triangle is a = ½. Number Of Triangles Formed In A Pentagon.
From slideplayer.com
ANGLES OF POLYGONS SECTION 81 JIM SMITH JCHS. ppt download Number Of Triangles Formed In A Pentagon $bd$, $be$ form $6+11=17$ triangles. The area for a triangle is a = ½ × base × height. First, we count the number of triangles with all three vertices on the pentagon. Notice that any set of three points on the pentagon will form a triangle. The formula for the area of a rectangle is a = length × width.. Number Of Triangles Formed In A Pentagon.
From www.lifewire.com
Polygon Geometry Pentagons, Hexagons and Dodecagons Number Of Triangles Formed In A Pentagon Consider a regular polygon with. The formula for the area of a rectangle is a = length × width. The pattern developed in the example above, is consistent for all polygons. Note that there are other formulas for the area of a triangle. Notice that any set of three points on the pentagon will form a triangle. The triangles of. Number Of Triangles Formed In A Pentagon.
From www.cuemath.com
Angles in a Pentagon Definitions, Formulas, Solved Examples Number Of Triangles Formed In A Pentagon $bd$, $be$ form $6+11=17$ triangles. Note that there are other formulas for the area of a triangle. Notice that any set of three points on the pentagon will form a triangle. First, we count the number of triangles with all three vertices on the pentagon. The triangles of a polygon are the triangles created by drawing line segments from one. Number Of Triangles Formed In A Pentagon.
From sites.google.com
Math to think about... Mrs Hinds Classroom site Number Of Triangles Formed In A Pentagon Notice that any set of three points on the pentagon will form a triangle. $bd$, $be$ form $6+11=17$ triangles. Using that, you get (n choose 3) as the number of possible triangles that can be formed by the vertices of a regular polygon of n sides. The area for a triangle is a = ½ × base × height. Note. Number Of Triangles Formed In A Pentagon.
From www.edplace.com
Calculate Angle Sizes Within Polygons Worksheet EdPlace Number Of Triangles Formed In A Pentagon The formula for the area of a rectangle is a = length × width. First, we count the number of triangles with all three vertices on the pentagon. The number of triangles formed by $ac$, $ad$ is $1+2=3$. The pattern developed in the example above, is consistent for all polygons. Consider a regular polygon with. Note that there are other. Number Of Triangles Formed In A Pentagon.
From www.slideserve.com
PPT NAMING POLYGONS PowerPoint Presentation, free download ID1399337 Number Of Triangles Formed In A Pentagon The pattern developed in the example above, is consistent for all polygons. The number of triangles formed by $ac$, $ad$ is $1+2=3$. First, we count the number of triangles with all three vertices on the pentagon. In the adjoining figure of a pentagon abcde, on joining ac and ad, the given pentagon is. Triangles of a polygon definition: Note that. Number Of Triangles Formed In A Pentagon.
From www.cuemath.com
Pentagon Shape Definition, Properties, Formulas, Examples Number Of Triangles Formed In A Pentagon Note that there are other formulas for the area of a triangle. The formula for the area of a rectangle is a = length × width. In the adjoining figure of a pentagon abcde, on joining ac and ad, the given pentagon is. Notice that any set of three points on the pentagon will form a triangle. First, we count. Number Of Triangles Formed In A Pentagon.
From www.coursehero.com
[Solved] Please walk me through these questions. Step 1 In each polygon,... Course Hero Number Of Triangles Formed In A Pentagon First, we count the number of triangles with all three vertices on the pentagon. The number of triangles formed by $ac$, $ad$ is $1+2=3$. Triangles of a polygon definition: The pattern developed in the example above, is consistent for all polygons. Using that, you get (n choose 3) as the number of possible triangles that can be formed by the. Number Of Triangles Formed In A Pentagon.
From theusinfo.netlify.app
How Many Triangles Are In A Pentagram Number Of Triangles Formed In A Pentagon The number of triangles formed by $ac$, $ad$ is $1+2=3$. Using that, you get (n choose 3) as the number of possible triangles that can be formed by the vertices of a regular polygon of n sides. In the adjoining figure of a pentagon abcde, on joining ac and ad, the given pentagon is. The pattern developed in the example. Number Of Triangles Formed In A Pentagon.
From mathmonks.com
Pentagon Definition, Shape, Properties, Formulas Number Of Triangles Formed In A Pentagon Note that there are other formulas for the area of a triangle. The area for a triangle is a = ½ × base × height. The triangles of a polygon are the triangles created by drawing line segments from one vertex of a polygon to all. In the adjoining figure of a pentagon abcde, on joining ac and ad, the. Number Of Triangles Formed In A Pentagon.