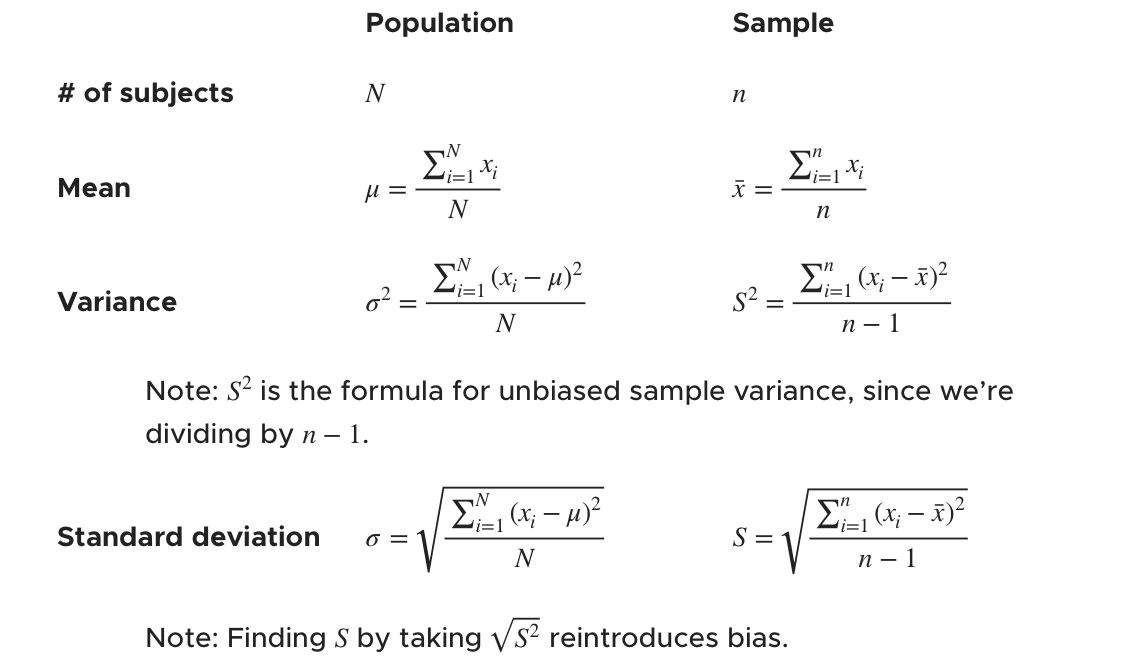
Geometry Sample Variance . (the sample variance) to describe the variability in the data. It would be nice to have a. The variance of a geometric random variable \(x\) is: For example, using rank revealing qr decomposition (rrqr)[1] provides some information regarding the sample variance for data points in. With p variable,need p variances and p(p 1)/2 covariances. To find the variance, we are going to use that trick of. In the negative binomial experiment, set \(k = 1\) to get the geometric distribution. Vary \(p\) with the scroll bar and note the location and. Beginning from the definition of sample variance: In this section, we establish some essential properties of the sample variance and standard deviation. \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\) \(\bar{x}=\dfrac{1}{n}\sum\limits_{i=1}^n x_i\) is the sample mean of the.
from www.kristakingmath.com
In this section, we establish some essential properties of the sample variance and standard deviation. With p variable,need p variances and p(p 1)/2 covariances. To find the variance, we are going to use that trick of. In the negative binomial experiment, set \(k = 1\) to get the geometric distribution. For example, using rank revealing qr decomposition (rrqr)[1] provides some information regarding the sample variance for data points in. The variance of a geometric random variable \(x\) is: \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\) \(\bar{x}=\dfrac{1}{n}\sum\limits_{i=1}^n x_i\) is the sample mean of the. Beginning from the definition of sample variance: (the sample variance) to describe the variability in the data. It would be nice to have a.
How to find Mean, variance, and standard deviation — Krista King Math
Geometry Sample Variance Vary \(p\) with the scroll bar and note the location and. To find the variance, we are going to use that trick of. It would be nice to have a. (the sample variance) to describe the variability in the data. \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\) \(\bar{x}=\dfrac{1}{n}\sum\limits_{i=1}^n x_i\) is the sample mean of the. Beginning from the definition of sample variance: In the negative binomial experiment, set \(k = 1\) to get the geometric distribution. The variance of a geometric random variable \(x\) is: For example, using rank revealing qr decomposition (rrqr)[1] provides some information regarding the sample variance for data points in. With p variable,need p variances and p(p 1)/2 covariances. Vary \(p\) with the scroll bar and note the location and. In this section, we establish some essential properties of the sample variance and standard deviation.
From www.youtube.com
Sample Variance and Standard Deviation Formula Explained! YouTube Geometry Sample Variance (the sample variance) to describe the variability in the data. With p variable,need p variances and p(p 1)/2 covariances. Vary \(p\) with the scroll bar and note the location and. In the negative binomial experiment, set \(k = 1\) to get the geometric distribution. Beginning from the definition of sample variance: It would be nice to have a. \(x_1, x_2,. Geometry Sample Variance.
From mathsathome.com
How to Calculate Variance Geometry Sample Variance Vary \(p\) with the scroll bar and note the location and. With p variable,need p variances and p(p 1)/2 covariances. Beginning from the definition of sample variance: (the sample variance) to describe the variability in the data. To find the variance, we are going to use that trick of. \(x_1, x_2, \ldots, x_n\) are observations of a random sample of. Geometry Sample Variance.
From quantitative-probabilitydistribution.blogspot.com
Variance Of The Probability Distribution Research Topics Geometry Sample Variance In the negative binomial experiment, set \(k = 1\) to get the geometric distribution. It would be nice to have a. To find the variance, we are going to use that trick of. \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\) \(\bar{x}=\dfrac{1}{n}\sum\limits_{i=1}^n x_i\) is the sample mean of the.. Geometry Sample Variance.
From www.slideserve.com
PPT Measures of Variability PowerPoint Presentation, free download Geometry Sample Variance (the sample variance) to describe the variability in the data. \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\) \(\bar{x}=\dfrac{1}{n}\sum\limits_{i=1}^n x_i\) is the sample mean of the. To find the variance, we are going to use that trick of. For example, using rank revealing qr decomposition (rrqr)[1] provides some information. Geometry Sample Variance.
From www.slideserve.com
PPT Measures of Variability PowerPoint Presentation, free download Geometry Sample Variance The variance of a geometric random variable \(x\) is: In the negative binomial experiment, set \(k = 1\) to get the geometric distribution. To find the variance, we are going to use that trick of. For example, using rank revealing qr decomposition (rrqr)[1] provides some information regarding the sample variance for data points in. In this section, we establish some. Geometry Sample Variance.
From mathsathome.com
How to Calculate Variance Geometry Sample Variance In this section, we establish some essential properties of the sample variance and standard deviation. In the negative binomial experiment, set \(k = 1\) to get the geometric distribution. Vary \(p\) with the scroll bar and note the location and. The variance of a geometric random variable \(x\) is: With p variable,need p variances and p(p 1)/2 covariances. To find. Geometry Sample Variance.
From www.sampletemplates.com
FREE 14+ Sample Variances Templates in MS Word PDF Geometry Sample Variance It would be nice to have a. In the negative binomial experiment, set \(k = 1\) to get the geometric distribution. (the sample variance) to describe the variability in the data. \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\) \(\bar{x}=\dfrac{1}{n}\sum\limits_{i=1}^n x_i\) is the sample mean of the. For example,. Geometry Sample Variance.
From www.wikihow.com
3 Ways to Calculate Variance wikiHow Geometry Sample Variance In the negative binomial experiment, set \(k = 1\) to get the geometric distribution. In this section, we establish some essential properties of the sample variance and standard deviation. It would be nice to have a. \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\) \(\bar{x}=\dfrac{1}{n}\sum\limits_{i=1}^n x_i\) is the sample. Geometry Sample Variance.
From mrs-mathpedia.com
The Variance and Standard Deviation Mrs.Mathpedia Geometry Sample Variance In the negative binomial experiment, set \(k = 1\) to get the geometric distribution. It would be nice to have a. With p variable,need p variances and p(p 1)/2 covariances. For example, using rank revealing qr decomposition (rrqr)[1] provides some information regarding the sample variance for data points in. \(x_1, x_2, \ldots, x_n\) are observations of a random sample of. Geometry Sample Variance.
From mathsathome.com
How to Calculate Variance Geometry Sample Variance Beginning from the definition of sample variance: Vary \(p\) with the scroll bar and note the location and. To find the variance, we are going to use that trick of. For example, using rank revealing qr decomposition (rrqr)[1] provides some information regarding the sample variance for data points in. In the negative binomial experiment, set \(k = 1\) to get. Geometry Sample Variance.
From mathsathome.com
How to Calculate Variance Geometry Sample Variance \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\) \(\bar{x}=\dfrac{1}{n}\sum\limits_{i=1}^n x_i\) is the sample mean of the. In the negative binomial experiment, set \(k = 1\) to get the geometric distribution. Beginning from the definition of sample variance: To find the variance, we are going to use that trick of.. Geometry Sample Variance.
From www.knowhowadda.com
How to Calculate Variance knowhowadda Geometry Sample Variance Beginning from the definition of sample variance: In this section, we establish some essential properties of the sample variance and standard deviation. It would be nice to have a. The variance of a geometric random variable \(x\) is: Vary \(p\) with the scroll bar and note the location and. For example, using rank revealing qr decomposition (rrqr)[1] provides some information. Geometry Sample Variance.
From slidetodoc.com
MEASURES OF VARIABILITY Variance Population variance Sample variance Geometry Sample Variance (the sample variance) to describe the variability in the data. In this section, we establish some essential properties of the sample variance and standard deviation. To find the variance, we are going to use that trick of. The variance of a geometric random variable \(x\) is: For example, using rank revealing qr decomposition (rrqr)[1] provides some information regarding the sample. Geometry Sample Variance.
From www.slideserve.com
PPT Frequency Distribution Mean, Variance, Standard Deviation Geometry Sample Variance Beginning from the definition of sample variance: It would be nice to have a. In the negative binomial experiment, set \(k = 1\) to get the geometric distribution. To find the variance, we are going to use that trick of. Vary \(p\) with the scroll bar and note the location and. \(x_1, x_2, \ldots, x_n\) are observations of a random. Geometry Sample Variance.
From mr-mathematics.com
Variance of Discrete Random Variables Geometry Sample Variance Vary \(p\) with the scroll bar and note the location and. The variance of a geometric random variable \(x\) is: (the sample variance) to describe the variability in the data. It would be nice to have a. In this section, we establish some essential properties of the sample variance and standard deviation. With p variable,need p variances and p(p 1)/2. Geometry Sample Variance.
From www.slideserve.com
PPT The Mean Variance Standard Deviation and ZScores PowerPoint Geometry Sample Variance Vary \(p\) with the scroll bar and note the location and. With p variable,need p variances and p(p 1)/2 covariances. For example, using rank revealing qr decomposition (rrqr)[1] provides some information regarding the sample variance for data points in. Beginning from the definition of sample variance: In the negative binomial experiment, set \(k = 1\) to get the geometric distribution.. Geometry Sample Variance.
From www.slideserve.com
PPT Measures of Variability PowerPoint Presentation, free download Geometry Sample Variance With p variable,need p variances and p(p 1)/2 covariances. It would be nice to have a. Vary \(p\) with the scroll bar and note the location and. Beginning from the definition of sample variance: \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\) \(\bar{x}=\dfrac{1}{n}\sum\limits_{i=1}^n x_i\) is the sample mean of. Geometry Sample Variance.
From www.kristakingmath.com
How to find Mean, variance, and standard deviation — Krista King Math Geometry Sample Variance In the negative binomial experiment, set \(k = 1\) to get the geometric distribution. With p variable,need p variances and p(p 1)/2 covariances. (the sample variance) to describe the variability in the data. The variance of a geometric random variable \(x\) is: Vary \(p\) with the scroll bar and note the location and. It would be nice to have a.. Geometry Sample Variance.
From www.cuemath.com
Sample Variance Formula Learn the sample variance formula Cuemath Geometry Sample Variance For example, using rank revealing qr decomposition (rrqr)[1] provides some information regarding the sample variance for data points in. It would be nice to have a. The variance of a geometric random variable \(x\) is: With p variable,need p variances and p(p 1)/2 covariances. Beginning from the definition of sample variance: (the sample variance) to describe the variability in the. Geometry Sample Variance.
From teachoo.com
Example 9 Find variance and standard deviation Class 11 Geometry Sample Variance It would be nice to have a. The variance of a geometric random variable \(x\) is: With p variable,need p variances and p(p 1)/2 covariances. To find the variance, we are going to use that trick of. In this section, we establish some essential properties of the sample variance and standard deviation. In the negative binomial experiment, set \(k =. Geometry Sample Variance.
From mathsathome.com
How to Calculate Variance Geometry Sample Variance The variance of a geometric random variable \(x\) is: It would be nice to have a. Vary \(p\) with the scroll bar and note the location and. To find the variance, we are going to use that trick of. In the negative binomial experiment, set \(k = 1\) to get the geometric distribution. \(x_1, x_2, \ldots, x_n\) are observations of. Geometry Sample Variance.
From www.qualitygurus.com
One Sample Variance Test (Chisquare) Quality Gurus Geometry Sample Variance In this section, we establish some essential properties of the sample variance and standard deviation. The variance of a geometric random variable \(x\) is: In the negative binomial experiment, set \(k = 1\) to get the geometric distribution. \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\) \(\bar{x}=\dfrac{1}{n}\sum\limits_{i=1}^n x_i\) is. Geometry Sample Variance.
From www.youtube.com
Understanding the Variance and Standard Deviation YouTube Geometry Sample Variance \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\) \(\bar{x}=\dfrac{1}{n}\sum\limits_{i=1}^n x_i\) is the sample mean of the. Beginning from the definition of sample variance: Vary \(p\) with the scroll bar and note the location and. (the sample variance) to describe the variability in the data. In the negative binomial experiment,. Geometry Sample Variance.
From www.youtube.com
Two ways to calculate the the sample variance YouTube Geometry Sample Variance In the negative binomial experiment, set \(k = 1\) to get the geometric distribution. For example, using rank revealing qr decomposition (rrqr)[1] provides some information regarding the sample variance for data points in. The variance of a geometric random variable \(x\) is: To find the variance, we are going to use that trick of. Beginning from the definition of sample. Geometry Sample Variance.
From www.inchcalculator.com
Variance Calculator (with Steps) Inch Calculator Geometry Sample Variance It would be nice to have a. To find the variance, we are going to use that trick of. Beginning from the definition of sample variance: (the sample variance) to describe the variability in the data. \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\) \(\bar{x}=\dfrac{1}{n}\sum\limits_{i=1}^n x_i\) is the sample. Geometry Sample Variance.
From www.slideserve.com
PPT BASIC NOTATION PowerPoint Presentation, free download ID6286712 Geometry Sample Variance For example, using rank revealing qr decomposition (rrqr)[1] provides some information regarding the sample variance for data points in. Beginning from the definition of sample variance: To find the variance, we are going to use that trick of. (the sample variance) to describe the variability in the data. With p variable,need p variances and p(p 1)/2 covariances. Vary \(p\) with. Geometry Sample Variance.
From dxomtgkbb.blob.core.windows.net
Sample Variance Of X at Kelly Cecil blog Geometry Sample Variance It would be nice to have a. With p variable,need p variances and p(p 1)/2 covariances. \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\) \(\bar{x}=\dfrac{1}{n}\sum\limits_{i=1}^n x_i\) is the sample mean of the. The variance of a geometric random variable \(x\) is: In the negative binomial experiment, set \(k =. Geometry Sample Variance.
From www.slideserve.com
PPT Sample variance and sample error PowerPoint Presentation, free Geometry Sample Variance To find the variance, we are going to use that trick of. It would be nice to have a. In the negative binomial experiment, set \(k = 1\) to get the geometric distribution. \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\) \(\bar{x}=\dfrac{1}{n}\sum\limits_{i=1}^n x_i\) is the sample mean of the.. Geometry Sample Variance.
From articles.outlier.org
How To Calculate Variance In 4 Simple Steps Outlier Geometry Sample Variance The variance of a geometric random variable \(x\) is: Beginning from the definition of sample variance: \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\) \(\bar{x}=\dfrac{1}{n}\sum\limits_{i=1}^n x_i\) is the sample mean of the. (the sample variance) to describe the variability in the data. It would be nice to have a.. Geometry Sample Variance.
From www.slideserve.com
PPT Measures of Variability PowerPoint Presentation, free download Geometry Sample Variance For example, using rank revealing qr decomposition (rrqr)[1] provides some information regarding the sample variance for data points in. In this section, we establish some essential properties of the sample variance and standard deviation. It would be nice to have a. (the sample variance) to describe the variability in the data. In the negative binomial experiment, set \(k = 1\). Geometry Sample Variance.
From mathsathome.com
How to Calculate Variance Geometry Sample Variance Beginning from the definition of sample variance: Vary \(p\) with the scroll bar and note the location and. In the negative binomial experiment, set \(k = 1\) to get the geometric distribution. With p variable,need p variances and p(p 1)/2 covariances. (the sample variance) to describe the variability in the data. The variance of a geometric random variable \(x\) is:. Geometry Sample Variance.
From www.slideserve.com
PPT Measures of Variation PowerPoint Presentation, free download ID Geometry Sample Variance In this section, we establish some essential properties of the sample variance and standard deviation. To find the variance, we are going to use that trick of. With p variable,need p variances and p(p 1)/2 covariances. (the sample variance) to describe the variability in the data. Vary \(p\) with the scroll bar and note the location and. It would be. Geometry Sample Variance.
From www.slideserve.com
PPT Sample Geometry and Random Sampling PowerPoint Presentation, free Geometry Sample Variance Beginning from the definition of sample variance: With p variable,need p variances and p(p 1)/2 covariances. It would be nice to have a. In this section, we establish some essential properties of the sample variance and standard deviation. To find the variance, we are going to use that trick of. The variance of a geometric random variable \(x\) is: \(x_1,. Geometry Sample Variance.
From www.slideserve.com
PPT The Mean Variance Standard Deviation and ZScores PowerPoint Geometry Sample Variance To find the variance, we are going to use that trick of. (the sample variance) to describe the variability in the data. \(x_1, x_2, \ldots, x_n\) are observations of a random sample of size \(n\) from the normal distribution \(n(\mu, \sigma^2)\) \(\bar{x}=\dfrac{1}{n}\sum\limits_{i=1}^n x_i\) is the sample mean of the. With p variable,need p variances and p(p 1)/2 covariances. In this. Geometry Sample Variance.
From www.youtube.com
How To Calculate Variance YouTube Geometry Sample Variance It would be nice to have a. In the negative binomial experiment, set \(k = 1\) to get the geometric distribution. For example, using rank revealing qr decomposition (rrqr)[1] provides some information regarding the sample variance for data points in. (the sample variance) to describe the variability in the data. In this section, we establish some essential properties of the. Geometry Sample Variance.