Magnetic Field Of Bent Wire . $$b = \frac{\mu\cdot i}{2 \cdot \pi \cdot r^2} r$$ it grows linearly with the radius. This law enables us to calculate the magnitude and direction of the magnetic field produced by a current in a wire. Determine the dependence of the magnetic field from a thin, straight wire based on the distance from it and the current flowing in the wire. As explained here, the magnetix field generated by a thick conductor is equal to: In summary, the task is to determine the magnetic field at the center of an arc formed by a bend in a long straight wire carrying current i. Understanding the magnetic fields produced by curved wires is vital in electromagnetism. Each straight section is 2.0 m long and makes an angle of θ = 60 o with the x axis,. The bent wire shown in figure lies in a uniform magnetic field.
from www.doubtnut.com
Determine the dependence of the magnetic field from a thin, straight wire based on the distance from it and the current flowing in the wire. As explained here, the magnetix field generated by a thick conductor is equal to: This law enables us to calculate the magnitude and direction of the magnetic field produced by a current in a wire. $$b = \frac{\mu\cdot i}{2 \cdot \pi \cdot r^2} r$$ it grows linearly with the radius. Each straight section is 2.0 m long and makes an angle of θ = 60 o with the x axis,. The bent wire shown in figure lies in a uniform magnetic field. In summary, the task is to determine the magnetic field at the center of an arc formed by a bend in a long straight wire carrying current i. Understanding the magnetic fields produced by curved wires is vital in electromagnetism.
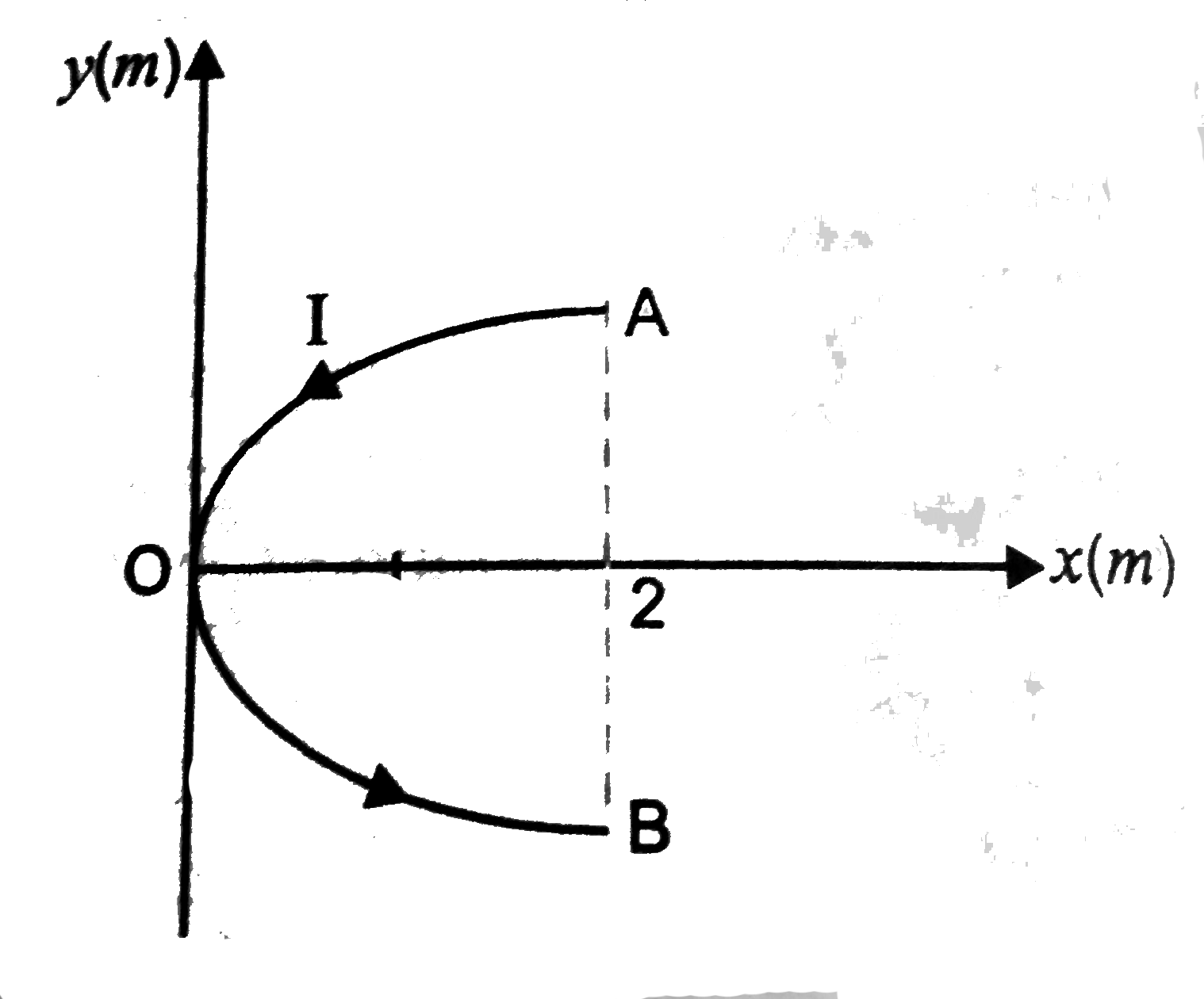
A conducting wire bent in the from of a parabola y^(2)=2x carries a cu
Magnetic Field Of Bent Wire As explained here, the magnetix field generated by a thick conductor is equal to: As explained here, the magnetix field generated by a thick conductor is equal to: Determine the dependence of the magnetic field from a thin, straight wire based on the distance from it and the current flowing in the wire. This law enables us to calculate the magnitude and direction of the magnetic field produced by a current in a wire. The bent wire shown in figure lies in a uniform magnetic field. $$b = \frac{\mu\cdot i}{2 \cdot \pi \cdot r^2} r$$ it grows linearly with the radius. In summary, the task is to determine the magnetic field at the center of an arc formed by a bend in a long straight wire carrying current i. Understanding the magnetic fields produced by curved wires is vital in electromagnetism. Each straight section is 2.0 m long and makes an angle of θ = 60 o with the x axis,.
From www.youtube.com
Field using BiotSavart law Circular Loop and Long Wire YouTube Magnetic Field Of Bent Wire Determine the dependence of the magnetic field from a thin, straight wire based on the distance from it and the current flowing in the wire. In summary, the task is to determine the magnetic field at the center of an arc formed by a bend in a long straight wire carrying current i. This law enables us to calculate the. Magnetic Field Of Bent Wire.
From www.doubtnut.com
A conducting wire bent in the from of a parabola y^(2)=2x carries a cu Magnetic Field Of Bent Wire Each straight section is 2.0 m long and makes an angle of θ = 60 o with the x axis,. As explained here, the magnetix field generated by a thick conductor is equal to: The bent wire shown in figure lies in a uniform magnetic field. This law enables us to calculate the magnitude and direction of the magnetic field. Magnetic Field Of Bent Wire.
From www.youtube.com
Field of a Straight Current Carrying Wire YouTube Magnetic Field Of Bent Wire This law enables us to calculate the magnitude and direction of the magnetic field produced by a current in a wire. $$b = \frac{\mu\cdot i}{2 \cdot \pi \cdot r^2} r$$ it grows linearly with the radius. In summary, the task is to determine the magnetic field at the center of an arc formed by a bend in a long straight. Magnetic Field Of Bent Wire.
From www.numerade.com
The bent wire shown in Fig. 2825 lies in a uniform field Magnetic Field Of Bent Wire The bent wire shown in figure lies in a uniform magnetic field. Determine the dependence of the magnetic field from a thin, straight wire based on the distance from it and the current flowing in the wire. In summary, the task is to determine the magnetic field at the center of an arc formed by a bend in a long. Magnetic Field Of Bent Wire.
From byjus.com
A long wire carries a steady current. It is bent into a circle of one Magnetic Field Of Bent Wire Determine the dependence of the magnetic field from a thin, straight wire based on the distance from it and the current flowing in the wire. In summary, the task is to determine the magnetic field at the center of an arc formed by a bend in a long straight wire carrying current i. $$b = \frac{\mu\cdot i}{2 \cdot \pi \cdot. Magnetic Field Of Bent Wire.
From www.slideserve.com
PPT ELECTRODYNAMICS PowerPoint Presentation ID162570 Magnetic Field Of Bent Wire $$b = \frac{\mu\cdot i}{2 \cdot \pi \cdot r^2} r$$ it grows linearly with the radius. Each straight section is 2.0 m long and makes an angle of θ = 60 o with the x axis,. Determine the dependence of the magnetic field from a thin, straight wire based on the distance from it and the current flowing in the wire.. Magnetic Field Of Bent Wire.
From www.doubtnut.com
A flexible wire bent in the form of a circle is placed in a uniform ma Magnetic Field Of Bent Wire Each straight section is 2.0 m long and makes an angle of θ = 60 o with the x axis,. This law enables us to calculate the magnitude and direction of the magnetic field produced by a current in a wire. $$b = \frac{\mu\cdot i}{2 \cdot \pi \cdot r^2} r$$ it grows linearly with the radius. Determine the dependence of. Magnetic Field Of Bent Wire.
From www.numerade.com
SOLVED Biot Savart III field due to a bent infinitely long Magnetic Field Of Bent Wire As explained here, the magnetix field generated by a thick conductor is equal to: This law enables us to calculate the magnitude and direction of the magnetic field produced by a current in a wire. Each straight section is 2.0 m long and makes an angle of θ = 60 o with the x axis,. The bent wire shown in. Magnetic Field Of Bent Wire.
From www.doubtnut.com
A long wire is bent as shown in Fig. what will be the magnitude and di Magnetic Field Of Bent Wire As explained here, the magnetix field generated by a thick conductor is equal to: In summary, the task is to determine the magnetic field at the center of an arc formed by a bend in a long straight wire carrying current i. $$b = \frac{\mu\cdot i}{2 \cdot \pi \cdot r^2} r$$ it grows linearly with the radius. The bent wire. Magnetic Field Of Bent Wire.
From www.youtube.com
Field Due to a Straight Wire Lecture 2 YouTube Magnetic Field Of Bent Wire Understanding the magnetic fields produced by curved wires is vital in electromagnetism. In summary, the task is to determine the magnetic field at the center of an arc formed by a bend in a long straight wire carrying current i. This law enables us to calculate the magnitude and direction of the magnetic field produced by a current in a. Magnetic Field Of Bent Wire.
From www.numerade.com
SOLVED Problem 4 A wire bent into a semicircular loop of radius R Magnetic Field Of Bent Wire Each straight section is 2.0 m long and makes an angle of θ = 60 o with the x axis,. As explained here, the magnetix field generated by a thick conductor is equal to: Determine the dependence of the magnetic field from a thin, straight wire based on the distance from it and the current flowing in the wire. Understanding. Magnetic Field Of Bent Wire.
From www.youtube.com
Field Created by a Curved Wire YouTube Magnetic Field Of Bent Wire In summary, the task is to determine the magnetic field at the center of an arc formed by a bend in a long straight wire carrying current i. The bent wire shown in figure lies in a uniform magnetic field. As explained here, the magnetix field generated by a thick conductor is equal to: Determine the dependence of the magnetic. Magnetic Field Of Bent Wire.
From www.youtube.com
A long wire carrying a steady current is bent into a circular loop of Magnetic Field Of Bent Wire As explained here, the magnetix field generated by a thick conductor is equal to: Each straight section is 2.0 m long and makes an angle of θ = 60 o with the x axis,. $$b = \frac{\mu\cdot i}{2 \cdot \pi \cdot r^2} r$$ it grows linearly with the radius. In summary, the task is to determine the magnetic field at. Magnetic Field Of Bent Wire.
From www.toppr.com
14. Compute the magnitude and direction of the field the Magnetic Field Of Bent Wire As explained here, the magnetix field generated by a thick conductor is equal to: The bent wire shown in figure lies in a uniform magnetic field. Determine the dependence of the magnetic field from a thin, straight wire based on the distance from it and the current flowing in the wire. $$b = \frac{\mu\cdot i}{2 \cdot \pi \cdot r^2} r$$. Magnetic Field Of Bent Wire.
From guidepartwhiskered.z13.web.core.windows.net
Field Around A Wire Diagram Magnetic Field Of Bent Wire Determine the dependence of the magnetic field from a thin, straight wire based on the distance from it and the current flowing in the wire. In summary, the task is to determine the magnetic field at the center of an arc formed by a bend in a long straight wire carrying current i. This law enables us to calculate the. Magnetic Field Of Bent Wire.
From www.doubtnut.com
Figure shows a long wire bent at the middle to form a right angle. Sho Magnetic Field Of Bent Wire The bent wire shown in figure lies in a uniform magnetic field. As explained here, the magnetix field generated by a thick conductor is equal to: This law enables us to calculate the magnitude and direction of the magnetic field produced by a current in a wire. Determine the dependence of the magnetic field from a thin, straight wire based. Magnetic Field Of Bent Wire.
From www.chegg.com
Solved A wire, bent into a rectangle with sides a = 0.015 m Magnetic Field Of Bent Wire $$b = \frac{\mu\cdot i}{2 \cdot \pi \cdot r^2} r$$ it grows linearly with the radius. Understanding the magnetic fields produced by curved wires is vital in electromagnetism. In summary, the task is to determine the magnetic field at the center of an arc formed by a bend in a long straight wire carrying current i. This law enables us to. Magnetic Field Of Bent Wire.
From solvedlib.com
A very long wire is bent into the shape shown in the … SolvedLib Magnetic Field Of Bent Wire This law enables us to calculate the magnitude and direction of the magnetic field produced by a current in a wire. Each straight section is 2.0 m long and makes an angle of θ = 60 o with the x axis,. As explained here, the magnetix field generated by a thick conductor is equal to: Understanding the magnetic fields produced. Magnetic Field Of Bent Wire.
From www.doubtnut.com
A conducting wire is bent in the form of a n sided regular polygon Magnetic Field Of Bent Wire $$b = \frac{\mu\cdot i}{2 \cdot \pi \cdot r^2} r$$ it grows linearly with the radius. Understanding the magnetic fields produced by curved wires is vital in electromagnetism. Determine the dependence of the magnetic field from a thin, straight wire based on the distance from it and the current flowing in the wire. In summary, the task is to determine the. Magnetic Field Of Bent Wire.
From www.youtube.com
Force on a Bent Wire YouTube Magnetic Field Of Bent Wire Determine the dependence of the magnetic field from a thin, straight wire based on the distance from it and the current flowing in the wire. As explained here, the magnetix field generated by a thick conductor is equal to: Each straight section is 2.0 m long and makes an angle of θ = 60 o with the x axis,. The. Magnetic Field Of Bent Wire.
From www.chegg.com
Solved B4. (a) A wire bent into a semicircle of radius R Magnetic Field Of Bent Wire Understanding the magnetic fields produced by curved wires is vital in electromagnetism. Determine the dependence of the magnetic field from a thin, straight wire based on the distance from it and the current flowing in the wire. The bent wire shown in figure lies in a uniform magnetic field. This law enables us to calculate the magnitude and direction of. Magnetic Field Of Bent Wire.
From byjus.com
Figure 35 E4 shows a long wire bent at the middle to form a right angle Magnetic Field Of Bent Wire Understanding the magnetic fields produced by curved wires is vital in electromagnetism. This law enables us to calculate the magnitude and direction of the magnetic field produced by a current in a wire. Each straight section is 2.0 m long and makes an angle of θ = 60 o with the x axis,. As explained here, the magnetix field generated. Magnetic Field Of Bent Wire.
From www.toppr.com
A wire bent as shown in Figure carries a current I . Find the Magnetic Field Of Bent Wire Understanding the magnetic fields produced by curved wires is vital in electromagnetism. As explained here, the magnetix field generated by a thick conductor is equal to: The bent wire shown in figure lies in a uniform magnetic field. $$b = \frac{\mu\cdot i}{2 \cdot \pi \cdot r^2} r$$ it grows linearly with the radius. This law enables us to calculate the. Magnetic Field Of Bent Wire.
From www.chegg.com
Solved The bent wire shown in the figure lies in uniform Magnetic Field Of Bent Wire As explained here, the magnetix field generated by a thick conductor is equal to: In summary, the task is to determine the magnetic field at the center of an arc formed by a bend in a long straight wire carrying current i. This law enables us to calculate the magnitude and direction of the magnetic field produced by a current. Magnetic Field Of Bent Wire.
From www.toppr.com
A straight wire carrying a current of 5A us bent a semicircular arc of Magnetic Field Of Bent Wire Understanding the magnetic fields produced by curved wires is vital in electromagnetism. The bent wire shown in figure lies in a uniform magnetic field. Determine the dependence of the magnetic field from a thin, straight wire based on the distance from it and the current flowing in the wire. This law enables us to calculate the magnitude and direction of. Magnetic Field Of Bent Wire.
From www.doubtnut.com
A wire is bent into the shape shown in fig and the field is m Magnetic Field Of Bent Wire In summary, the task is to determine the magnetic field at the center of an arc formed by a bend in a long straight wire carrying current i. The bent wire shown in figure lies in a uniform magnetic field. Understanding the magnetic fields produced by curved wires is vital in electromagnetism. Determine the dependence of the magnetic field from. Magnetic Field Of Bent Wire.
From www.animalia-life.club
Field Of A Wire Magnetic Field Of Bent Wire This law enables us to calculate the magnitude and direction of the magnetic field produced by a current in a wire. $$b = \frac{\mu\cdot i}{2 \cdot \pi \cdot r^2} r$$ it grows linearly with the radius. The bent wire shown in figure lies in a uniform magnetic field. In summary, the task is to determine the magnetic field at the. Magnetic Field Of Bent Wire.
From www.doubtnut.com
A current flows in the wire bent to form a hexagon loop of side 'a' Magnetic Field Of Bent Wire This law enables us to calculate the magnitude and direction of the magnetic field produced by a current in a wire. As explained here, the magnetix field generated by a thick conductor is equal to: The bent wire shown in figure lies in a uniform magnetic field. In summary, the task is to determine the magnetic field at the center. Magnetic Field Of Bent Wire.
From www.doubtnut.com
The wire shown in figure carries a current of 10A. Determine the magni Magnetic Field Of Bent Wire $$b = \frac{\mu\cdot i}{2 \cdot \pi \cdot r^2} r$$ it grows linearly with the radius. Determine the dependence of the magnetic field from a thin, straight wire based on the distance from it and the current flowing in the wire. In summary, the task is to determine the magnetic field at the center of an arc formed by a bend. Magnetic Field Of Bent Wire.
From www.youtube.com
3 biot savart law bent wire YouTube Magnetic Field Of Bent Wire The bent wire shown in figure lies in a uniform magnetic field. Determine the dependence of the magnetic field from a thin, straight wire based on the distance from it and the current flowing in the wire. As explained here, the magnetix field generated by a thick conductor is equal to: This law enables us to calculate the magnitude and. Magnetic Field Of Bent Wire.
From byjus.com
In the given diagram, a single infinitely long, straight wire has been Magnetic Field Of Bent Wire In summary, the task is to determine the magnetic field at the center of an arc formed by a bend in a long straight wire carrying current i. As explained here, the magnetix field generated by a thick conductor is equal to: Understanding the magnetic fields produced by curved wires is vital in electromagnetism. $$b = \frac{\mu\cdot i}{2 \cdot \pi. Magnetic Field Of Bent Wire.
From www.toppr.com
A long wire carrying a steady current is bent into a circular loop of Magnetic Field Of Bent Wire This law enables us to calculate the magnitude and direction of the magnetic field produced by a current in a wire. Each straight section is 2.0 m long and makes an angle of θ = 60 o with the x axis,. As explained here, the magnetix field generated by a thick conductor is equal to: $$b = \frac{\mu\cdot i}{2 \cdot. Magnetic Field Of Bent Wire.
From www.toppr.com
A wire bent as shown in Figure carries a current I . Find the Magnetic Field Of Bent Wire Determine the dependence of the magnetic field from a thin, straight wire based on the distance from it and the current flowing in the wire. Each straight section is 2.0 m long and makes an angle of θ = 60 o with the x axis,. This law enables us to calculate the magnitude and direction of the magnetic field produced. Magnetic Field Of Bent Wire.
From www.numerade.com
An infinitely long wire carrying a current I is bent at a right angle Magnetic Field Of Bent Wire $$b = \frac{\mu\cdot i}{2 \cdot \pi \cdot r^2} r$$ it grows linearly with the radius. Determine the dependence of the magnetic field from a thin, straight wire based on the distance from it and the current flowing in the wire. In summary, the task is to determine the magnetic field at the center of an arc formed by a bend. Magnetic Field Of Bent Wire.
From www.youtube.com
field by bent finite length wire YouTube Magnetic Field Of Bent Wire Each straight section is 2.0 m long and makes an angle of θ = 60 o with the x axis,. Determine the dependence of the magnetic field from a thin, straight wire based on the distance from it and the current flowing in the wire. The bent wire shown in figure lies in a uniform magnetic field. Understanding the magnetic. Magnetic Field Of Bent Wire.