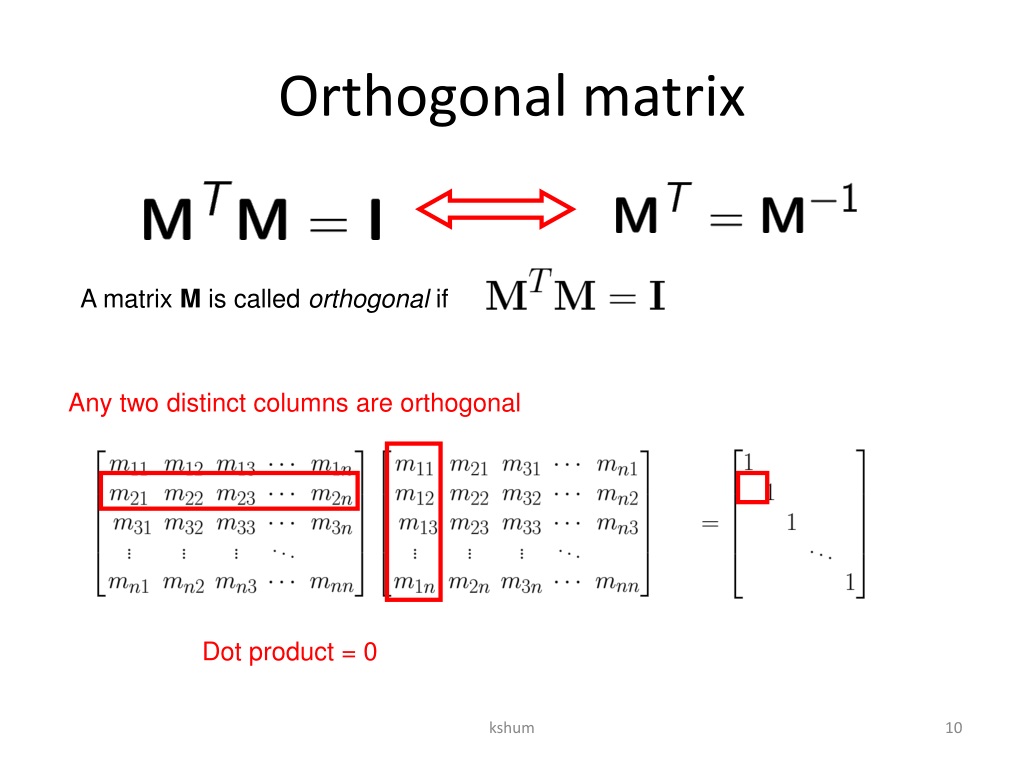
Matrix Orthogonal Equation at Vincent Womack blog

Matrix Orthogonal Equation. Likewise for the row vectors. In other words, the transpose of an orthogonal. Learn the orthogonal matrix definition and its properties. Matrices with orthonormal columns are a new class of important matri ces to add to those on our list: A matrix a ∈ gl. N (r) is orthogonal if av · aw = v · w for all vectors v and w. When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called an orthogonal matrix. The precise definition is as follows. Learn more about the orthogonal. Also, learn how to identify the given matrix is an orthogonal matrix with solved. Also, the product of an orthogonal matrix and its transpose is equal to i. An orthogonal matrix \(u\), from definition 4.11.7, is one in which \(uu^{t} = i\). (1) a matrix is orthogonal exactly when its column vectors have length one, and are pairwise orthogonal; In particular, taking v = w means that lengths are preserved by orthogonal. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose.

Likewise for the row vectors. Also, the product of an orthogonal matrix and its transpose is equal to i. A matrix a ∈ gl. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. N (r) is orthogonal if av · aw = v · w for all vectors v and w. In particular, taking v = w means that lengths are preserved by orthogonal. The precise definition is as follows. When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called an orthogonal matrix. Learn more about the orthogonal. Matrices with orthonormal columns are a new class of important matri ces to add to those on our list:

PPT ENGG2013 Unit 19 The principal axes theorem PowerPoint

Matrix Orthogonal Equation A matrix a ∈ gl. Learn the orthogonal matrix definition and its properties. In particular, taking v = w means that lengths are preserved by orthogonal. N (r) is orthogonal if av · aw = v · w for all vectors v and w. Likewise for the row vectors. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. (1) a matrix is orthogonal exactly when its column vectors have length one, and are pairwise orthogonal; Learn more about the orthogonal. A matrix a ∈ gl. In other words, the transpose of an orthogonal. When an \(n \times n\) matrix has all real entries and its transpose equals its inverse, the matrix is called an orthogonal matrix. The precise definition is as follows. Matrices with orthonormal columns are a new class of important matri ces to add to those on our list: An orthogonal matrix \(u\), from definition 4.11.7, is one in which \(uu^{t} = i\). Also, learn how to identify the given matrix is an orthogonal matrix with solved. Also, the product of an orthogonal matrix and its transpose is equal to i.