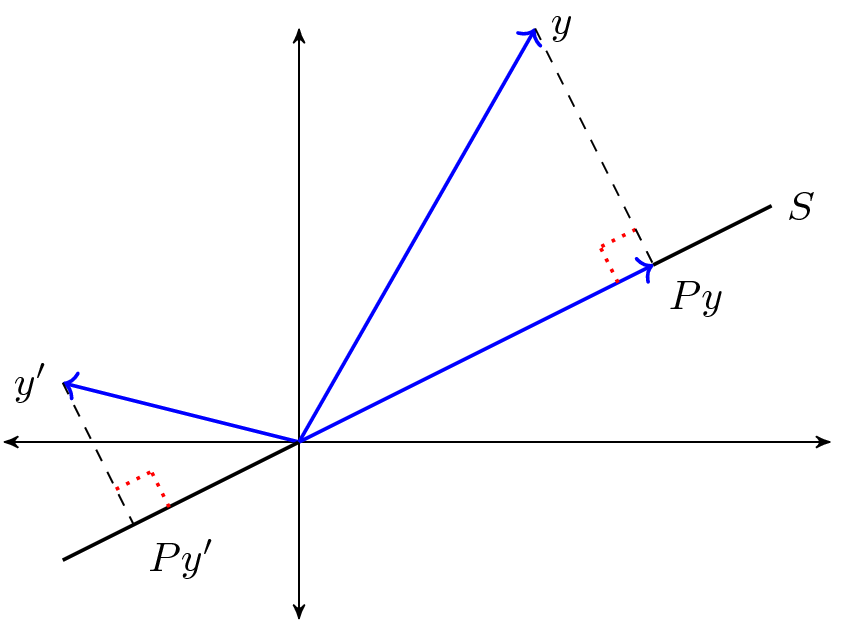Matlab Orthogonal Projection . Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. In this lab you will use matlab to study the following topics: Find the length (or norm) of the vector that is the orthogonal projection of the vector a = [ 1 2 4 ] onto b = [6 10 3]. This is a perspective projection on a plane tangent at the center point from an infinite distance (that is, orthogonally). Let us denote your point as $(x_0,y_0,z_0)$ instead of $(x,y,z)$ and projection as $(x'_0,y'_0,z'_0)$ parametric equation of the. Norm, dot product, and orthogonal projection. I need to calculate the orthogonal projection of the point x= (3.5,1.5,−1.5) on the plane 4x−4y+4z=12 and also calculate the. Differentiate the distance squared with respect to lambda and. The center point is a pole in the common polar aspect, but can. • geometric aspects of vectors: The projection of a point q = (x, y, z) onto a plane given by a point p = (a, b, c) and a normal n = (d, e, f) is.
from julia.quantecon.org
In this lab you will use matlab to study the following topics: • geometric aspects of vectors: The center point is a pole in the common polar aspect, but can. I need to calculate the orthogonal projection of the point x= (3.5,1.5,−1.5) on the plane 4x−4y+4z=12 and also calculate the. Differentiate the distance squared with respect to lambda and. Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. Norm, dot product, and orthogonal projection. Find the length (or norm) of the vector that is the orthogonal projection of the vector a = [ 1 2 4 ] onto b = [6 10 3]. Let us denote your point as $(x_0,y_0,z_0)$ instead of $(x,y,z)$ and projection as $(x'_0,y'_0,z'_0)$ parametric equation of the. The projection of a point q = (x, y, z) onto a plane given by a point p = (a, b, c) and a normal n = (d, e, f) is.
16. Orthogonal Projections and Their Applications — Quantitative
Matlab Orthogonal Projection In this lab you will use matlab to study the following topics: Norm, dot product, and orthogonal projection. The center point is a pole in the common polar aspect, but can. Find the length (or norm) of the vector that is the orthogonal projection of the vector a = [ 1 2 4 ] onto b = [6 10 3]. Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. In this lab you will use matlab to study the following topics: Let us denote your point as $(x_0,y_0,z_0)$ instead of $(x,y,z)$ and projection as $(x'_0,y'_0,z'_0)$ parametric equation of the. I need to calculate the orthogonal projection of the point x= (3.5,1.5,−1.5) on the plane 4x−4y+4z=12 and also calculate the. • geometric aspects of vectors: This is a perspective projection on a plane tangent at the center point from an infinite distance (that is, orthogonally). The projection of a point q = (x, y, z) onto a plane given by a point p = (a, b, c) and a normal n = (d, e, f) is. Differentiate the distance squared with respect to lambda and.
From www.developpez.net
Projection orthogonale MATLAB Matlab Orthogonal Projection This is a perspective projection on a plane tangent at the center point from an infinite distance (that is, orthogonally). I need to calculate the orthogonal projection of the point x= (3.5,1.5,−1.5) on the plane 4x−4y+4z=12 and also calculate the. Differentiate the distance squared with respect to lambda and. The center point is a pole in the common polar aspect,. Matlab Orthogonal Projection.
From www.slideserve.com
PPT Karmarkar Algorithm PowerPoint Presentation, free download ID Matlab Orthogonal Projection Let us denote your point as $(x_0,y_0,z_0)$ instead of $(x,y,z)$ and projection as $(x'_0,y'_0,z'_0)$ parametric equation of the. This is a perspective projection on a plane tangent at the center point from an infinite distance (that is, orthogonally). • geometric aspects of vectors: Norm, dot product, and orthogonal projection. Differentiate the distance squared with respect to lambda and. Find the. Matlab Orthogonal Projection.
From www.demonstrations.wolfram.com
Orthogonal Projections of the Edges of a Cube Wolfram Demonstrations Matlab Orthogonal Projection This is a perspective projection on a plane tangent at the center point from an infinite distance (that is, orthogonally). Let us denote your point as $(x_0,y_0,z_0)$ instead of $(x,y,z)$ and projection as $(x'_0,y'_0,z'_0)$ parametric equation of the. • geometric aspects of vectors: Differentiate the distance squared with respect to lambda and. Norm, dot product, and orthogonal projection. Learn the. Matlab Orthogonal Projection.
From www.youtube.com
Orthogonal Projection (+ Examples) YouTube Matlab Orthogonal Projection The projection of a point q = (x, y, z) onto a plane given by a point p = (a, b, c) and a normal n = (d, e, f) is. I need to calculate the orthogonal projection of the point x= (3.5,1.5,−1.5) on the plane 4x−4y+4z=12 and also calculate the. Let us denote your point as $(x_0,y_0,z_0)$ instead of. Matlab Orthogonal Projection.
From sites.wcsu.edu
Orthogonal Projections and Curve Fitting Matlab Orthogonal Projection In this lab you will use matlab to study the following topics: This is a perspective projection on a plane tangent at the center point from an infinite distance (that is, orthogonally). Find the length (or norm) of the vector that is the orthogonal projection of the vector a = [ 1 2 4 ] onto b = [6 10. Matlab Orthogonal Projection.
From byjus.com
28. The orthogonal projection( the locus of foot of perpendicular from Matlab Orthogonal Projection In this lab you will use matlab to study the following topics: I need to calculate the orthogonal projection of the point x= (3.5,1.5,−1.5) on the plane 4x−4y+4z=12 and also calculate the. The projection of a point q = (x, y, z) onto a plane given by a point p = (a, b, c) and a normal n = (d,. Matlab Orthogonal Projection.
From www.slideserve.com
PPT Projection PowerPoint Presentation, free download ID6879351 Matlab Orthogonal Projection The center point is a pole in the common polar aspect, but can. Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. In this lab you will use matlab to study the following topics: The projection of a point q = (x, y, z) onto a plane given by a point p = (a, b,. Matlab Orthogonal Projection.
From www.numerade.com
Input the following matrix into Matlab P=(1)/(2)([1,1,1,1,1],[1,1,1,1 Matlab Orthogonal Projection Find the length (or norm) of the vector that is the orthogonal projection of the vector a = [ 1 2 4 ] onto b = [6 10 3]. The projection of a point q = (x, y, z) onto a plane given by a point p = (a, b, c) and a normal n = (d, e, f) is.. Matlab Orthogonal Projection.
From 9to5answer.com
[Solved] Formula for a orthogonal projection matrix? 9to5Answer Matlab Orthogonal Projection The projection of a point q = (x, y, z) onto a plane given by a point p = (a, b, c) and a normal n = (d, e, f) is. • geometric aspects of vectors: Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. Find the length (or norm) of the vector that is. Matlab Orthogonal Projection.
From www.theengineerspost.com
A Beginners Guide to Orthographic Projection [Engineering Drawing] Matlab Orthogonal Projection Let us denote your point as $(x_0,y_0,z_0)$ instead of $(x,y,z)$ and projection as $(x'_0,y'_0,z'_0)$ parametric equation of the. Differentiate the distance squared with respect to lambda and. Find the length (or norm) of the vector that is the orthogonal projection of the vector a = [ 1 2 4 ] onto b = [6 10 3]. Learn the basic properties. Matlab Orthogonal Projection.
From julia.quantecon.org
16. Orthogonal Projections and Their Applications — Quantitative Matlab Orthogonal Projection Find the length (or norm) of the vector that is the orthogonal projection of the vector a = [ 1 2 4 ] onto b = [6 10 3]. In this lab you will use matlab to study the following topics: This is a perspective projection on a plane tangent at the center point from an infinite distance (that is,. Matlab Orthogonal Projection.
From www.vrogue.co
Standard Matrix Of A Orthogonal Projection Linear Tra vrogue.co Matlab Orthogonal Projection The projection of a point q = (x, y, z) onto a plane given by a point p = (a, b, c) and a normal n = (d, e, f) is. I need to calculate the orthogonal projection of the point x= (3.5,1.5,−1.5) on the plane 4x−4y+4z=12 and also calculate the. • geometric aspects of vectors: Norm, dot product, and. Matlab Orthogonal Projection.
From www.geogebra.org
Orthogonal Projection GeoGebra Matlab Orthogonal Projection Norm, dot product, and orthogonal projection. Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. In this lab you will use matlab to study the following topics: • geometric aspects of vectors: The center point is a pole in the common polar aspect, but can. Differentiate the distance squared with respect to lambda and. I. Matlab Orthogonal Projection.
From www.researchgate.net
The orthogonal projection of two separated convex polytopes, A and B Matlab Orthogonal Projection The center point is a pole in the common polar aspect, but can. Norm, dot product, and orthogonal projection. Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. The projection of a point q = (x, y, z) onto a plane given by a point p = (a, b, c) and a normal n =. Matlab Orthogonal Projection.
From uk.mathworks.com
Spherical Coordinates MATLAB & Simulink MathWorks United Kingdom Matlab Orthogonal Projection Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. • geometric aspects of vectors: In this lab you will use matlab to study the following topics: This is a perspective projection on a plane tangent at the center point from an infinite distance (that is, orthogonally). Let us denote your point as $(x_0,y_0,z_0)$ instead of. Matlab Orthogonal Projection.
From slidetodoc.com
Orthogonal Vector Hungyi Lee Orthogonal Set A set Matlab Orthogonal Projection The projection of a point q = (x, y, z) onto a plane given by a point p = (a, b, c) and a normal n = (d, e, f) is. In this lab you will use matlab to study the following topics: • geometric aspects of vectors: Norm, dot product, and orthogonal projection. Find the length (or norm) of. Matlab Orthogonal Projection.
From www.researchgate.net
Orthogonal projection of the tooltip onto a geometric curve Matlab Orthogonal Projection • geometric aspects of vectors: I need to calculate the orthogonal projection of the point x= (3.5,1.5,−1.5) on the plane 4x−4y+4z=12 and also calculate the. Find the length (or norm) of the vector that is the orthogonal projection of the vector a = [ 1 2 4 ] onto b = [6 10 3]. This is a perspective projection on. Matlab Orthogonal Projection.
From heung-bae-lee.github.io
Least Squares Problem & Orthogonal Projection DataLatte's IT Blog Matlab Orthogonal Projection Differentiate the distance squared with respect to lambda and. Norm, dot product, and orthogonal projection. This is a perspective projection on a plane tangent at the center point from an infinite distance (that is, orthogonally). Let us denote your point as $(x_0,y_0,z_0)$ instead of $(x,y,z)$ and projection as $(x'_0,y'_0,z'_0)$ parametric equation of the. Learn the basic properties of orthogonal projections. Matlab Orthogonal Projection.
From www.slideserve.com
PPT 5.1 Orthogonal Projections PowerPoint Presentation, free download Matlab Orthogonal Projection Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. I need to calculate the orthogonal projection of the point x= (3.5,1.5,−1.5) on the plane 4x−4y+4z=12 and also calculate the. Differentiate the distance squared with respect to lambda and. • geometric aspects of vectors: This is a perspective projection on a plane tangent at the center. Matlab Orthogonal Projection.
From www.ideamoocs.com
Orthographic Projections IDEA Institute Matlab Orthogonal Projection This is a perspective projection on a plane tangent at the center point from an infinite distance (that is, orthogonally). In this lab you will use matlab to study the following topics: Let us denote your point as $(x_0,y_0,z_0)$ instead of $(x,y,z)$ and projection as $(x'_0,y'_0,z'_0)$ parametric equation of the. The projection of a point q = (x, y, z). Matlab Orthogonal Projection.
From civilmint.com
Orthographic Projection Definition, Examples, And Types Matlab Orthogonal Projection Find the length (or norm) of the vector that is the orthogonal projection of the vector a = [ 1 2 4 ] onto b = [6 10 3]. • geometric aspects of vectors: Norm, dot product, and orthogonal projection. This is a perspective projection on a plane tangent at the center point from an infinite distance (that is, orthogonally).. Matlab Orthogonal Projection.
From www.youtube.com
Calculus 3 Vector Projections & Orthogonal Components YouTube Matlab Orthogonal Projection Find the length (or norm) of the vector that is the orthogonal projection of the vector a = [ 1 2 4 ] onto b = [6 10 3]. Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. Norm, dot product, and orthogonal projection. I need to calculate the orthogonal projection of the point x=. Matlab Orthogonal Projection.
From www.demonstrations.wolfram.com
Orthogonal Projections of the Edges of a Cube Wolfram Demonstrations Matlab Orthogonal Projection I need to calculate the orthogonal projection of the point x= (3.5,1.5,−1.5) on the plane 4x−4y+4z=12 and also calculate the. Find the length (or norm) of the vector that is the orthogonal projection of the vector a = [ 1 2 4 ] onto b = [6 10 3]. Norm, dot product, and orthogonal projection. This is a perspective projection. Matlab Orthogonal Projection.
From www.zpag.net
Projections orthogonales normalisation Matlab Orthogonal Projection The projection of a point q = (x, y, z) onto a plane given by a point p = (a, b, c) and a normal n = (d, e, f) is. This is a perspective projection on a plane tangent at the center point from an infinite distance (that is, orthogonally). Norm, dot product, and orthogonal projection. Differentiate the distance. Matlab Orthogonal Projection.
From www.researchgate.net
Orthogonal axis projection principle. Download Scientific Diagram Matlab Orthogonal Projection In this lab you will use matlab to study the following topics: Find the length (or norm) of the vector that is the orthogonal projection of the vector a = [ 1 2 4 ] onto b = [6 10 3]. • geometric aspects of vectors: The center point is a pole in the common polar aspect, but can. This. Matlab Orthogonal Projection.
From flowphysics.ucsd.edu
Streaming Spectral Proper Orthogonal (MATLAB Matlab Orthogonal Projection In this lab you will use matlab to study the following topics: Differentiate the distance squared with respect to lambda and. The projection of a point q = (x, y, z) onto a plane given by a point p = (a, b, c) and a normal n = (d, e, f) is. Norm, dot product, and orthogonal projection. Learn the. Matlab Orthogonal Projection.
From www.geogebra.org
Orthogonal Projection 3D GeoGebra Matlab Orthogonal Projection Find the length (or norm) of the vector that is the orthogonal projection of the vector a = [ 1 2 4 ] onto b = [6 10 3]. In this lab you will use matlab to study the following topics: I need to calculate the orthogonal projection of the point x= (3.5,1.5,−1.5) on the plane 4x−4y+4z=12 and also calculate. Matlab Orthogonal Projection.
From www.youtube.com
Orthogonal Collocation on Finite Elements in MATLAB YouTube Matlab Orthogonal Projection Norm, dot product, and orthogonal projection. Differentiate the distance squared with respect to lambda and. I need to calculate the orthogonal projection of the point x= (3.5,1.5,−1.5) on the plane 4x−4y+4z=12 and also calculate the. Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. • geometric aspects of vectors: Let us denote your point as. Matlab Orthogonal Projection.
From heung-bae-lee.github.io
Least Squares Problem & Orthogonal Projection DataLatte's IT Blog Matlab Orthogonal Projection Differentiate the distance squared with respect to lambda and. This is a perspective projection on a plane tangent at the center point from an infinite distance (that is, orthogonally). I need to calculate the orthogonal projection of the point x= (3.5,1.5,−1.5) on the plane 4x−4y+4z=12 and also calculate the. Find the length (or norm) of the vector that is the. Matlab Orthogonal Projection.
From www.cs.bu.edu
Orthogonal Sets and Projection — Linear Algebra, Geometry, and Computation Matlab Orthogonal Projection The projection of a point q = (x, y, z) onto a plane given by a point p = (a, b, c) and a normal n = (d, e, f) is. This is a perspective projection on a plane tangent at the center point from an infinite distance (that is, orthogonally). • geometric aspects of vectors: Find the length (or. Matlab Orthogonal Projection.
From www.youtube.com
Basics of Orthographic Projection Engineering Graphics YouTube Matlab Orthogonal Projection Differentiate the distance squared with respect to lambda and. This is a perspective projection on a plane tangent at the center point from an infinite distance (that is, orthogonally). Norm, dot product, and orthogonal projection. Let us denote your point as $(x_0,y_0,z_0)$ instead of $(x,y,z)$ and projection as $(x'_0,y'_0,z'_0)$ parametric equation of the. In this lab you will use matlab. Matlab Orthogonal Projection.
From calcworkshop.com
(Orthogonal Projection) Made Easy for Students Matlab Orthogonal Projection The center point is a pole in the common polar aspect, but can. Let us denote your point as $(x_0,y_0,z_0)$ instead of $(x,y,z)$ and projection as $(x'_0,y'_0,z'_0)$ parametric equation of the. Norm, dot product, and orthogonal projection. In this lab you will use matlab to study the following topics: I need to calculate the orthogonal projection of the point x=. Matlab Orthogonal Projection.
From www.slideserve.com
PPT The Projection Matrix PowerPoint Presentation, free download ID Matlab Orthogonal Projection In this lab you will use matlab to study the following topics: This is a perspective projection on a plane tangent at the center point from an infinite distance (that is, orthogonally). Norm, dot product, and orthogonal projection. Let us denote your point as $(x_0,y_0,z_0)$ instead of $(x,y,z)$ and projection as $(x'_0,y'_0,z'_0)$ parametric equation of the. The projection of a. Matlab Orthogonal Projection.
From topitanswers.com
Orthogonal Projection onto the Intersection of Convex Sets Convex Matlab Orthogonal Projection Learn the basic properties of orthogonal projections as linear transformations and as matrix transformations. Norm, dot product, and orthogonal projection. The projection of a point q = (x, y, z) onto a plane given by a point p = (a, b, c) and a normal n = (d, e, f) is. Find the length (or norm) of the vector that. Matlab Orthogonal Projection.
From www.researchgate.net
Orthogonal Projections to Latent Structures Discriminant Analysis Matlab Orthogonal Projection I need to calculate the orthogonal projection of the point x= (3.5,1.5,−1.5) on the plane 4x−4y+4z=12 and also calculate the. Find the length (or norm) of the vector that is the orthogonal projection of the vector a = [ 1 2 4 ] onto b = [6 10 3]. The center point is a pole in the common polar aspect,. Matlab Orthogonal Projection.