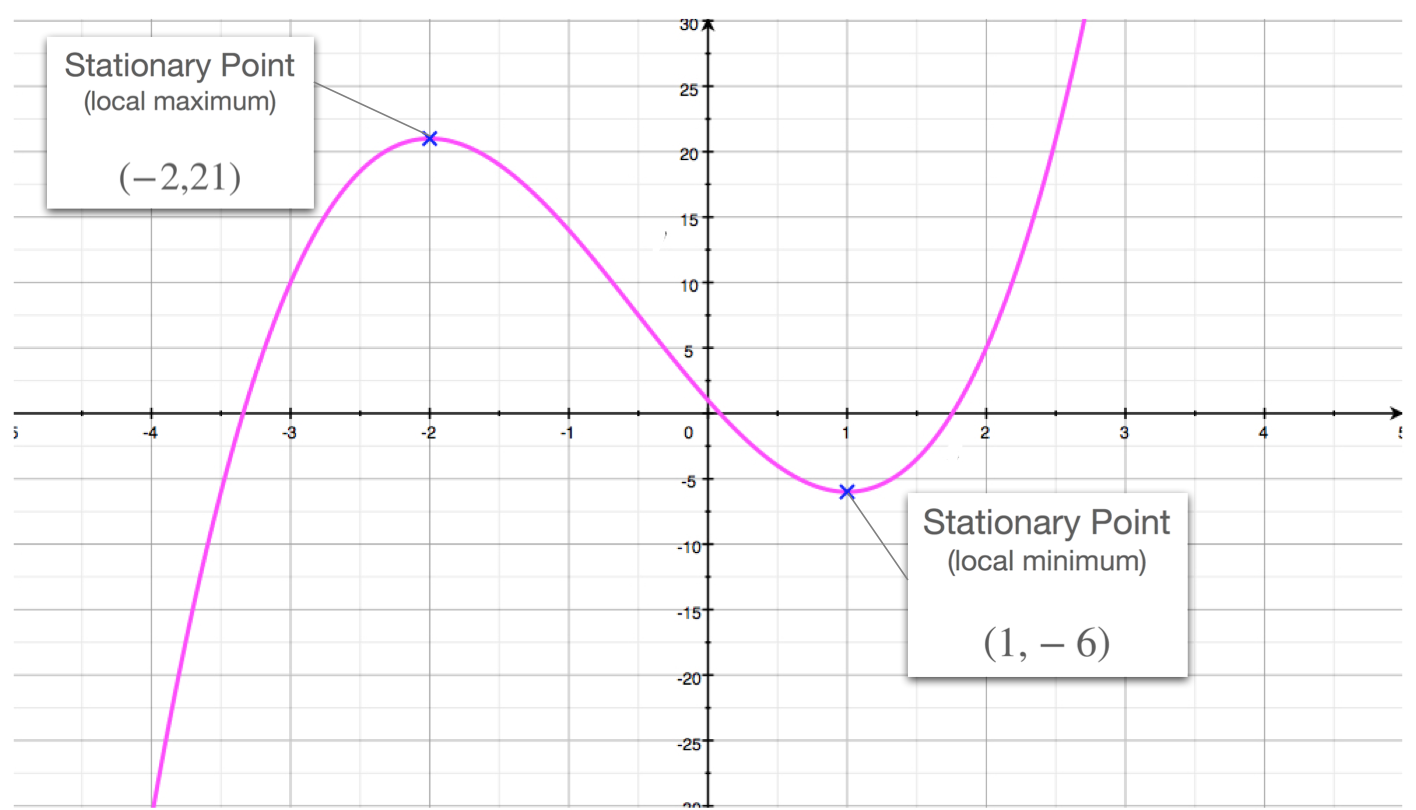
Stationary Points Definition . a stationary point of f(x1, x2,., xn)f (x1,x2,…,xn) is a point such that fxi = 0f xi = 0, for all i = 1, 2,.ni =1,2,…n. These points are called “stationary” because at. a stationary point refers to a point on a function where the derivative is zero, indicating that there is no change in the. illustrated definition of stationary point: a stationary point of a function $f(x)$ is a point where the derivative of $f(x)$ is equal to 0. This can be where the curve reaches a minimum or maximum. in a smoothly changing function a stationary point is a point where the function stops increasing or decreasing: stationary points occur where the first derivative of a function equals zero, which can indicate potential extrema. A point on a curve where the slope is zero.
from www.radfordmathematics.com
This can be where the curve reaches a minimum or maximum. A point on a curve where the slope is zero. a stationary point of a function $f(x)$ is a point where the derivative of $f(x)$ is equal to 0. stationary points occur where the first derivative of a function equals zero, which can indicate potential extrema. a stationary point of f(x1, x2,., xn)f (x1,x2,…,xn) is a point such that fxi = 0f xi = 0, for all i = 1, 2,.ni =1,2,…n. in a smoothly changing function a stationary point is a point where the function stops increasing or decreasing: These points are called “stationary” because at. a stationary point refers to a point on a function where the derivative is zero, indicating that there is no change in the. illustrated definition of stationary point:
Stationary Points
Stationary Points Definition A point on a curve where the slope is zero. a stationary point of a function $f(x)$ is a point where the derivative of $f(x)$ is equal to 0. a stationary point of f(x1, x2,., xn)f (x1,x2,…,xn) is a point such that fxi = 0f xi = 0, for all i = 1, 2,.ni =1,2,…n. in a smoothly changing function a stationary point is a point where the function stops increasing or decreasing: a stationary point refers to a point on a function where the derivative is zero, indicating that there is no change in the. These points are called “stationary” because at. A point on a curve where the slope is zero. This can be where the curve reaches a minimum or maximum. illustrated definition of stationary point: stationary points occur where the first derivative of a function equals zero, which can indicate potential extrema.
From bookdown.org
Chapter 9 Stationary Points MATH1006 Calculus Stationary Points Definition stationary points occur where the first derivative of a function equals zero, which can indicate potential extrema. a stationary point refers to a point on a function where the derivative is zero, indicating that there is no change in the. This can be where the curve reaches a minimum or maximum. A point on a curve where the. Stationary Points Definition.
From mathsathome.com
How to Find and Classify Stationary Points Stationary Points Definition A point on a curve where the slope is zero. These points are called “stationary” because at. in a smoothly changing function a stationary point is a point where the function stops increasing or decreasing: a stationary point of a function $f(x)$ is a point where the derivative of $f(x)$ is equal to 0. a stationary point. Stationary Points Definition.
From mathsathome.com
How to Find and Classify Stationary Points Stationary Points Definition a stationary point of f(x1, x2,., xn)f (x1,x2,…,xn) is a point such that fxi = 0f xi = 0, for all i = 1, 2,.ni =1,2,…n. a stationary point of a function $f(x)$ is a point where the derivative of $f(x)$ is equal to 0. a stationary point refers to a point on a function where the. Stationary Points Definition.
From mathsathome.com
How to Find and Classify Stationary Points Stationary Points Definition stationary points occur where the first derivative of a function equals zero, which can indicate potential extrema. illustrated definition of stationary point: a stationary point of a function $f(x)$ is a point where the derivative of $f(x)$ is equal to 0. These points are called “stationary” because at. A point on a curve where the slope is. Stationary Points Definition.
From www.slideserve.com
PPT Relative Extrema Graphing Polynomials PowerPoint Presentation Stationary Points Definition a stationary point of f(x1, x2,., xn)f (x1,x2,…,xn) is a point such that fxi = 0f xi = 0, for all i = 1, 2,.ni =1,2,…n. stationary points occur where the first derivative of a function equals zero, which can indicate potential extrema. illustrated definition of stationary point: a stationary point of a function $f(x)$ is. Stationary Points Definition.
From www.youtube.com
Stationary Points, Minimums & Maximums ALevel Maths YouTube Stationary Points Definition These points are called “stationary” because at. a stationary point of f(x1, x2,., xn)f (x1,x2,…,xn) is a point such that fxi = 0f xi = 0, for all i = 1, 2,.ni =1,2,…n. in a smoothly changing function a stationary point is a point where the function stops increasing or decreasing: illustrated definition of stationary point: . Stationary Points Definition.
From mistercorzi.scot
Tangents and stationary points Stationary Points Definition stationary points occur where the first derivative of a function equals zero, which can indicate potential extrema. a stationary point of a function $f(x)$ is a point where the derivative of $f(x)$ is equal to 0. This can be where the curve reaches a minimum or maximum. a stationary point of f(x1, x2,., xn)f (x1,x2,…,xn) is a. Stationary Points Definition.
From bookdown.org
Chapter 9 Stationary Points MATH1006 Calculus Stationary Points Definition This can be where the curve reaches a minimum or maximum. A point on a curve where the slope is zero. stationary points occur where the first derivative of a function equals zero, which can indicate potential extrema. a stationary point refers to a point on a function where the derivative is zero, indicating that there is no. Stationary Points Definition.
From mathsathome.com
How to Find and Classify Stationary Points Stationary Points Definition These points are called “stationary” because at. a stationary point refers to a point on a function where the derivative is zero, indicating that there is no change in the. a stationary point of f(x1, x2,., xn)f (x1,x2,…,xn) is a point such that fxi = 0f xi = 0, for all i = 1, 2,.ni =1,2,…n. This can. Stationary Points Definition.
From www.radfordmathematics.com
Stationary Points Stationary Points Definition stationary points occur where the first derivative of a function equals zero, which can indicate potential extrema. a stationary point refers to a point on a function where the derivative is zero, indicating that there is no change in the. illustrated definition of stationary point: This can be where the curve reaches a minimum or maximum. . Stationary Points Definition.
From bookdown.org
Chapter 9 Stationary Points MATH1006 Calculus Stationary Points Definition a stationary point of a function $f(x)$ is a point where the derivative of $f(x)$ is equal to 0. stationary points occur where the first derivative of a function equals zero, which can indicate potential extrema. a stationary point refers to a point on a function where the derivative is zero, indicating that there is no change. Stationary Points Definition.
From www.youtube.com
Stationary Points Corbettmaths YouTube Stationary Points Definition in a smoothly changing function a stationary point is a point where the function stops increasing or decreasing: illustrated definition of stationary point: This can be where the curve reaches a minimum or maximum. A point on a curve where the slope is zero. stationary points occur where the first derivative of a function equals zero, which. Stationary Points Definition.
From bookdown.org
Chapter 9 Stationary Points MATH1006 Calculus Stationary Points Definition stationary points occur where the first derivative of a function equals zero, which can indicate potential extrema. a stationary point of f(x1, x2,., xn)f (x1,x2,…,xn) is a point such that fxi = 0f xi = 0, for all i = 1, 2,.ni =1,2,…n. a stationary point of a function $f(x)$ is a point where the derivative of. Stationary Points Definition.
From www.slideserve.com
PPT Identifying Stationary Points PowerPoint Presentation, free Stationary Points Definition A point on a curve where the slope is zero. stationary points occur where the first derivative of a function equals zero, which can indicate potential extrema. in a smoothly changing function a stationary point is a point where the function stops increasing or decreasing: a stationary point of a function $f(x)$ is a point where the. Stationary Points Definition.
From corbettmaths.com
Stationary Points Video Corbettmaths Stationary Points Definition This can be where the curve reaches a minimum or maximum. a stationary point refers to a point on a function where the derivative is zero, indicating that there is no change in the. stationary points occur where the first derivative of a function equals zero, which can indicate potential extrema. a stationary point of a function. Stationary Points Definition.
From slideplayer.com
Derivatives in Action Chapter ppt download Stationary Points Definition stationary points occur where the first derivative of a function equals zero, which can indicate potential extrema. a stationary point of a function $f(x)$ is a point where the derivative of $f(x)$ is equal to 0. a stationary point refers to a point on a function where the derivative is zero, indicating that there is no change. Stationary Points Definition.
From www.slideshare.net
Stationary Points Handout Stationary Points Definition in a smoothly changing function a stationary point is a point where the function stops increasing or decreasing: These points are called “stationary” because at. illustrated definition of stationary point: a stationary point refers to a point on a function where the derivative is zero, indicating that there is no change in the. a stationary point. Stationary Points Definition.
From www.youtube.com
Critical Points Saddle Points Stationary Point and Point of Inflection Stationary Points Definition in a smoothly changing function a stationary point is a point where the function stops increasing or decreasing: A point on a curve where the slope is zero. illustrated definition of stationary point: stationary points occur where the first derivative of a function equals zero, which can indicate potential extrema. a stationary point refers to a. Stationary Points Definition.
From www.youtube.com
Types of Stationary Points and Testing YouTube Stationary Points Definition illustrated definition of stationary point: These points are called “stationary” because at. a stationary point refers to a point on a function where the derivative is zero, indicating that there is no change in the. in a smoothly changing function a stationary point is a point where the function stops increasing or decreasing: a stationary point. Stationary Points Definition.
From www.radfordmathematics.com
Stationary Points Stationary Points Definition a stationary point of f(x1, x2,., xn)f (x1,x2,…,xn) is a point such that fxi = 0f xi = 0, for all i = 1, 2,.ni =1,2,…n. in a smoothly changing function a stationary point is a point where the function stops increasing or decreasing: A point on a curve where the slope is zero. This can be where. Stationary Points Definition.
From mathsathome.com
How to Find and Classify Stationary Points Stationary Points Definition in a smoothly changing function a stationary point is a point where the function stops increasing or decreasing: A point on a curve where the slope is zero. These points are called “stationary” because at. a stationary point of f(x1, x2,., xn)f (x1,x2,…,xn) is a point such that fxi = 0f xi = 0, for all i =. Stationary Points Definition.
From www.radfordmathematics.com
Stationary Points Stationary Points Definition This can be where the curve reaches a minimum or maximum. A point on a curve where the slope is zero. illustrated definition of stationary point: a stationary point refers to a point on a function where the derivative is zero, indicating that there is no change in the. in a smoothly changing function a stationary point. Stationary Points Definition.
From bookdown.org
Chapter 9 Stationary Points MATH1006 Calculus Stationary Points Definition These points are called “stationary” because at. in a smoothly changing function a stationary point is a point where the function stops increasing or decreasing: stationary points occur where the first derivative of a function equals zero, which can indicate potential extrema. A point on a curve where the slope is zero. a stationary point refers to. Stationary Points Definition.
From mathsathome.com
How to Find and Classify Stationary Points Stationary Points Definition This can be where the curve reaches a minimum or maximum. stationary points occur where the first derivative of a function equals zero, which can indicate potential extrema. a stationary point of f(x1, x2,., xn)f (x1,x2,…,xn) is a point such that fxi = 0f xi = 0, for all i = 1, 2,.ni =1,2,…n. These points are called. Stationary Points Definition.
From www.radfordmathematics.com
Stationary Points Stationary Points Definition This can be where the curve reaches a minimum or maximum. a stationary point refers to a point on a function where the derivative is zero, indicating that there is no change in the. a stationary point of a function $f(x)$ is a point where the derivative of $f(x)$ is equal to 0. a stationary point of. Stationary Points Definition.
From www.youtube.com
How to Find the Coordinates of Stationary Points, f’(x)=0, Along a Stationary Points Definition stationary points occur where the first derivative of a function equals zero, which can indicate potential extrema. in a smoothly changing function a stationary point is a point where the function stops increasing or decreasing: A point on a curve where the slope is zero. illustrated definition of stationary point: This can be where the curve reaches. Stationary Points Definition.
From www.researchgate.net
Definition of stationary points, activationand reaction parameters on Stationary Points Definition a stationary point refers to a point on a function where the derivative is zero, indicating that there is no change in the. illustrated definition of stationary point: a stationary point of a function $f(x)$ is a point where the derivative of $f(x)$ is equal to 0. A point on a curve where the slope is zero.. Stationary Points Definition.
From mathsathome.com
How to Find and Classify Stationary Points Stationary Points Definition illustrated definition of stationary point: stationary points occur where the first derivative of a function equals zero, which can indicate potential extrema. These points are called “stationary” because at. a stationary point refers to a point on a function where the derivative is zero, indicating that there is no change in the. in a smoothly changing. Stationary Points Definition.
From bookdown.org
Chapter 9 Stationary Points MATH1006 Calculus Stationary Points Definition This can be where the curve reaches a minimum or maximum. stationary points occur where the first derivative of a function equals zero, which can indicate potential extrema. in a smoothly changing function a stationary point is a point where the function stops increasing or decreasing: These points are called “stationary” because at. a stationary point of. Stationary Points Definition.
From mathsathome.com
How to Find and Classify Stationary Points Stationary Points Definition illustrated definition of stationary point: in a smoothly changing function a stationary point is a point where the function stops increasing or decreasing: These points are called “stationary” because at. A point on a curve where the slope is zero. a stationary point refers to a point on a function where the derivative is zero, indicating that. Stationary Points Definition.
From doylemaths.weebly.com
Stationary Points Mathematics Tutorial Stationary Points Definition illustrated definition of stationary point: a stationary point of a function $f(x)$ is a point where the derivative of $f(x)$ is equal to 0. a stationary point refers to a point on a function where the derivative is zero, indicating that there is no change in the. A point on a curve where the slope is zero.. Stationary Points Definition.
From www.youtube.com
Types of Stationary Points YouTube Stationary Points Definition This can be where the curve reaches a minimum or maximum. stationary points occur where the first derivative of a function equals zero, which can indicate potential extrema. A point on a curve where the slope is zero. a stationary point refers to a point on a function where the derivative is zero, indicating that there is no. Stationary Points Definition.
From mathsmethods.com.au
Stationary Points in Maths Methods Stationary Points Definition a stationary point of f(x1, x2,., xn)f (x1,x2,…,xn) is a point such that fxi = 0f xi = 0, for all i = 1, 2,.ni =1,2,…n. a stationary point of a function $f(x)$ is a point where the derivative of $f(x)$ is equal to 0. This can be where the curve reaches a minimum or maximum. These points. Stationary Points Definition.
From mathsathome.com
How to Find and Classify Stationary Points Stationary Points Definition This can be where the curve reaches a minimum or maximum. a stationary point of f(x1, x2,., xn)f (x1,x2,…,xn) is a point such that fxi = 0f xi = 0, for all i = 1, 2,.ni =1,2,…n. A point on a curve where the slope is zero. illustrated definition of stationary point: a stationary point of a. Stationary Points Definition.
From www.radfordmathematics.com
Stationary Points Stationary Points Definition stationary points occur where the first derivative of a function equals zero, which can indicate potential extrema. This can be where the curve reaches a minimum or maximum. A point on a curve where the slope is zero. in a smoothly changing function a stationary point is a point where the function stops increasing or decreasing: a. Stationary Points Definition.