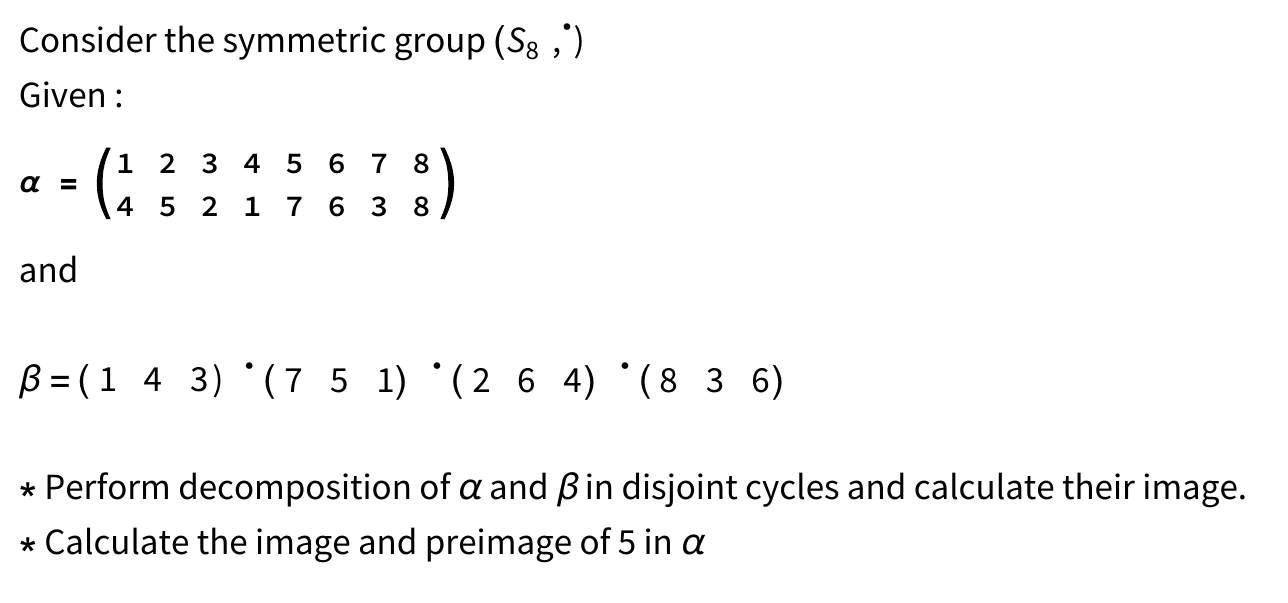Cycle Decomposition Examples . $\begin{pmatrix} 1 \end{pmatrix} \begin{pmatrix} 2 & 4 \end{pmatrix} \begin{pmatrix} 3 & 6 & 9. For instance, if ˇis the permutation in the previous example, we omit the cycle (3) in its disjoint cycle. Since the cycles of a permutation \(σ\) tell us \(σ(x)\) for every \(x\) in the domain of \(σ\), the cycle. F = (16325)(47)(8) the cycles can be. The cycle decomposition is f = (1,6,3,2,5)(4,7)(8) if all numbers are 1 digit, we may abbreviate: The cycle decomposition for $\rho$ is: Cycle decomposition of any permutation. This video demonstrates cycle notation in the symmetric group on 6 elements. The cyclic decomposition of a permutation can be computed in the wolfram language with the function permutationcycles[p]. We call the set of cycles of a permutation the cycle decomposition of the permutation. We also see a brief demonstration of cycle decomposition when composing.
from math.stackexchange.com
We also see a brief demonstration of cycle decomposition when composing. We call the set of cycles of a permutation the cycle decomposition of the permutation. This video demonstrates cycle notation in the symmetric group on 6 elements. For instance, if ˇis the permutation in the previous example, we omit the cycle (3) in its disjoint cycle. Since the cycles of a permutation \(σ\) tell us \(σ(x)\) for every \(x\) in the domain of \(σ\), the cycle. The cycle decomposition for $\rho$ is: The cyclic decomposition of a permutation can be computed in the wolfram language with the function permutationcycles[p]. Cycle decomposition of any permutation. F = (16325)(47)(8) the cycles can be. $\begin{pmatrix} 1 \end{pmatrix} \begin{pmatrix} 2 & 4 \end{pmatrix} \begin{pmatrix} 3 & 6 & 9.
discrete mathematics Help with disjoint cycle and
Cycle Decomposition Examples For instance, if ˇis the permutation in the previous example, we omit the cycle (3) in its disjoint cycle. The cyclic decomposition of a permutation can be computed in the wolfram language with the function permutationcycles[p]. The cycle decomposition for $\rho$ is: We call the set of cycles of a permutation the cycle decomposition of the permutation. This video demonstrates cycle notation in the symmetric group on 6 elements. We also see a brief demonstration of cycle decomposition when composing. F = (16325)(47)(8) the cycles can be. Cycle decomposition of any permutation. $\begin{pmatrix} 1 \end{pmatrix} \begin{pmatrix} 2 & 4 \end{pmatrix} \begin{pmatrix} 3 & 6 & 9. For instance, if ˇis the permutation in the previous example, we omit the cycle (3) in its disjoint cycle. Since the cycles of a permutation \(σ\) tell us \(σ(x)\) for every \(x\) in the domain of \(σ\), the cycle. The cycle decomposition is f = (1,6,3,2,5)(4,7)(8) if all numbers are 1 digit, we may abbreviate:
From www.youtube.com
Ecosystem Functioning and Process YouTube Cycle Decomposition Examples The cycle decomposition for $\rho$ is: We call the set of cycles of a permutation the cycle decomposition of the permutation. $\begin{pmatrix} 1 \end{pmatrix} \begin{pmatrix} 2 & 4 \end{pmatrix} \begin{pmatrix} 3 & 6 & 9. The cyclic decomposition of a permutation can be computed in the wolfram language with the function permutationcycles[p]. Cycle decomposition of any permutation. Since the cycles. Cycle Decomposition Examples.
From www.toppr.com
What is Write down its steps. Give a diagrammatic Cycle Decomposition Examples The cycle decomposition for $\rho$ is: For instance, if ˇis the permutation in the previous example, we omit the cycle (3) in its disjoint cycle. The cycle decomposition is f = (1,6,3,2,5)(4,7)(8) if all numbers are 1 digit, we may abbreviate: This video demonstrates cycle notation in the symmetric group on 6 elements. The cyclic decomposition of a permutation can. Cycle Decomposition Examples.
From www.youtube.com
Stages of Human YouTube Cycle Decomposition Examples Since the cycles of a permutation \(σ\) tell us \(σ(x)\) for every \(x\) in the domain of \(σ\), the cycle. We call the set of cycles of a permutation the cycle decomposition of the permutation. F = (16325)(47)(8) the cycles can be. Cycle decomposition of any permutation. The cycle decomposition for $\rho$ is: The cycle decomposition is f = (1,6,3,2,5)(4,7)(8). Cycle Decomposition Examples.
From www.slideserve.com
PPT The Requirements for Growth PowerPoint Presentation, free Cycle Decomposition Examples The cycle decomposition for $\rho$ is: We also see a brief demonstration of cycle decomposition when composing. F = (16325)(47)(8) the cycles can be. The cyclic decomposition of a permutation can be computed in the wolfram language with the function permutationcycles[p]. Cycle decomposition of any permutation. For instance, if ˇis the permutation in the previous example, we omit the cycle. Cycle Decomposition Examples.
From www.studypool.com
SOLUTION Cycle versus Linear Order Studypool Cycle Decomposition Examples The cyclic decomposition of a permutation can be computed in the wolfram language with the function permutationcycles[p]. The cycle decomposition is f = (1,6,3,2,5)(4,7)(8) if all numbers are 1 digit, we may abbreviate: This video demonstrates cycle notation in the symmetric group on 6 elements. We call the set of cycles of a permutation the cycle decomposition of the permutation.. Cycle Decomposition Examples.
From www.slideserve.com
PPT Packing Graphs with 4Cycles PowerPoint Presentation, free Cycle Decomposition Examples The cyclic decomposition of a permutation can be computed in the wolfram language with the function permutationcycles[p]. For instance, if ˇis the permutation in the previous example, we omit the cycle (3) in its disjoint cycle. We also see a brief demonstration of cycle decomposition when composing. $\begin{pmatrix} 1 \end{pmatrix} \begin{pmatrix} 2 & 4 \end{pmatrix} \begin{pmatrix} 3 & 6 &. Cycle Decomposition Examples.
From www.slideserve.com
PPT Cyclic and Bicyclic of the Complete Graph into the Cycle Decomposition Examples F = (16325)(47)(8) the cycles can be. Cycle decomposition of any permutation. Since the cycles of a permutation \(σ\) tell us \(σ(x)\) for every \(x\) in the domain of \(σ\), the cycle. The cycle decomposition for $\rho$ is: $\begin{pmatrix} 1 \end{pmatrix} \begin{pmatrix} 2 & 4 \end{pmatrix} \begin{pmatrix} 3 & 6 & 9. We also see a brief demonstration of cycle. Cycle Decomposition Examples.
From www.youtube.com
Lec49 Canonical cycle of permutations YouTube Cycle Decomposition Examples $\begin{pmatrix} 1 \end{pmatrix} \begin{pmatrix} 2 & 4 \end{pmatrix} \begin{pmatrix} 3 & 6 & 9. The cycle decomposition for $\rho$ is: For instance, if ˇis the permutation in the previous example, we omit the cycle (3) in its disjoint cycle. Since the cycles of a permutation \(σ\) tell us \(σ(x)\) for every \(x\) in the domain of \(σ\), the cycle. F. Cycle Decomposition Examples.
From www.researchgate.net
Diagrammatic description of cycle algorithm Download Cycle Decomposition Examples Since the cycles of a permutation \(σ\) tell us \(σ(x)\) for every \(x\) in the domain of \(σ\), the cycle. Cycle decomposition of any permutation. For instance, if ˇis the permutation in the previous example, we omit the cycle (3) in its disjoint cycle. F = (16325)(47)(8) the cycles can be. The cycle decomposition for $\rho$ is: We call the. Cycle Decomposition Examples.
From www.behance.net
Human Infographic on Behance Cycle Decomposition Examples We call the set of cycles of a permutation the cycle decomposition of the permutation. We also see a brief demonstration of cycle decomposition when composing. Cycle decomposition of any permutation. $\begin{pmatrix} 1 \end{pmatrix} \begin{pmatrix} 2 & 4 \end{pmatrix} \begin{pmatrix} 3 & 6 & 9. The cycle decomposition is f = (1,6,3,2,5)(4,7)(8) if all numbers are 1 digit, we may. Cycle Decomposition Examples.
From www.slideserve.com
PPT Math 3121 Abstract Algebra I PowerPoint Presentation, free Cycle Decomposition Examples F = (16325)(47)(8) the cycles can be. This video demonstrates cycle notation in the symmetric group on 6 elements. The cycle decomposition for $\rho$ is: $\begin{pmatrix} 1 \end{pmatrix} \begin{pmatrix} 2 & 4 \end{pmatrix} \begin{pmatrix} 3 & 6 & 9. We call the set of cycles of a permutation the cycle decomposition of the permutation. For instance, if ˇis the permutation. Cycle Decomposition Examples.
From math.stackexchange.com
discrete mathematics Help with disjoint cycle and Cycle Decomposition Examples The cyclic decomposition of a permutation can be computed in the wolfram language with the function permutationcycles[p]. We call the set of cycles of a permutation the cycle decomposition of the permutation. This video demonstrates cycle notation in the symmetric group on 6 elements. For instance, if ˇis the permutation in the previous example, we omit the cycle (3) in. Cycle Decomposition Examples.
From itsmyschoollibrary.com
Nitrogen Cycle And In Nature. SS2 Biology Lesson Note Cycle Decomposition Examples The cycle decomposition for $\rho$ is: For instance, if ˇis the permutation in the previous example, we omit the cycle (3) in its disjoint cycle. We call the set of cycles of a permutation the cycle decomposition of the permutation. F = (16325)(47)(8) the cycles can be. We also see a brief demonstration of cycle decomposition when composing. Cycle decomposition. Cycle Decomposition Examples.
From webapi.bu.edu
💌 Simple explanation of carbon cycle. Carbon cycle — Science Learning Cycle Decomposition Examples F = (16325)(47)(8) the cycles can be. The cycle decomposition for $\rho$ is: Cycle decomposition of any permutation. Since the cycles of a permutation \(σ\) tell us \(σ(x)\) for every \(x\) in the domain of \(σ\), the cycle. We call the set of cycles of a permutation the cycle decomposition of the permutation. We also see a brief demonstration of. Cycle Decomposition Examples.
From www.slideserve.com
PPT Packing Graphs with 4Cycles PowerPoint Presentation, free Cycle Decomposition Examples For instance, if ˇis the permutation in the previous example, we omit the cycle (3) in its disjoint cycle. F = (16325)(47)(8) the cycles can be. Cycle decomposition of any permutation. The cyclic decomposition of a permutation can be computed in the wolfram language with the function permutationcycles[p]. $\begin{pmatrix} 1 \end{pmatrix} \begin{pmatrix} 2 & 4 \end{pmatrix} \begin{pmatrix} 3 & 6. Cycle Decomposition Examples.
From www.biopassionate.net
Process Cycle Decomposition Examples The cycle decomposition for $\rho$ is: $\begin{pmatrix} 1 \end{pmatrix} \begin{pmatrix} 2 & 4 \end{pmatrix} \begin{pmatrix} 3 & 6 & 9. Cycle decomposition of any permutation. We call the set of cycles of a permutation the cycle decomposition of the permutation. For instance, if ˇis the permutation in the previous example, we omit the cycle (3) in its disjoint cycle. F. Cycle Decomposition Examples.
From www.youtube.com
What are Graph Graph Graph Theory Cycle Decomposition Examples We call the set of cycles of a permutation the cycle decomposition of the permutation. The cycle decomposition for $\rho$ is: F = (16325)(47)(8) the cycles can be. This video demonstrates cycle notation in the symmetric group on 6 elements. The cycle decomposition is f = (1,6,3,2,5)(4,7)(8) if all numbers are 1 digit, we may abbreviate: Cycle decomposition of any. Cycle Decomposition Examples.
From www.geeksforgeeks.org
CBSE Class 12 Cycle Decomposition Examples Since the cycles of a permutation \(σ\) tell us \(σ(x)\) for every \(x\) in the domain of \(σ\), the cycle. The cyclic decomposition of a permutation can be computed in the wolfram language with the function permutationcycles[p]. $\begin{pmatrix} 1 \end{pmatrix} \begin{pmatrix} 2 & 4 \end{pmatrix} \begin{pmatrix} 3 & 6 & 9. The cycle decomposition for $\rho$ is: For instance, if. Cycle Decomposition Examples.
From demonstrations.wolfram.com
Eulerian Tour and Cycle Wolfram Demonstrations Project Cycle Decomposition Examples We call the set of cycles of a permutation the cycle decomposition of the permutation. This video demonstrates cycle notation in the symmetric group on 6 elements. We also see a brief demonstration of cycle decomposition when composing. F = (16325)(47)(8) the cycles can be. Since the cycles of a permutation \(σ\) tell us \(σ(x)\) for every \(x\) in the. Cycle Decomposition Examples.
From www.researchgate.net
The of the process 1 DDFD Download Scientific Diagram Cycle Decomposition Examples F = (16325)(47)(8) the cycles can be. For instance, if ˇis the permutation in the previous example, we omit the cycle (3) in its disjoint cycle. Since the cycles of a permutation \(σ\) tell us \(σ(x)\) for every \(x\) in the domain of \(σ\), the cycle. The cyclic decomposition of a permutation can be computed in the wolfram language with. Cycle Decomposition Examples.
From www.biologyonline.com
Definition and Examples Biology Online Dictionary Cycle Decomposition Examples Since the cycles of a permutation \(σ\) tell us \(σ(x)\) for every \(x\) in the domain of \(σ\), the cycle. For instance, if ˇis the permutation in the previous example, we omit the cycle (3) in its disjoint cycle. $\begin{pmatrix} 1 \end{pmatrix} \begin{pmatrix} 2 & 4 \end{pmatrix} \begin{pmatrix} 3 & 6 & 9. The cyclic decomposition of a permutation can. Cycle Decomposition Examples.
From www.researchgate.net
Illustration of the cycle method, and data and keyframes Cycle Decomposition Examples $\begin{pmatrix} 1 \end{pmatrix} \begin{pmatrix} 2 & 4 \end{pmatrix} \begin{pmatrix} 3 & 6 & 9. Since the cycles of a permutation \(σ\) tell us \(σ(x)\) for every \(x\) in the domain of \(σ\), the cycle. F = (16325)(47)(8) the cycles can be. The cycle decomposition for $\rho$ is: The cycle decomposition is f = (1,6,3,2,5)(4,7)(8) if all numbers are 1 digit,. Cycle Decomposition Examples.
From www.pinterest.co.uk
River Bend Nature Center School Units Nutrient cycle Cycle Decomposition Examples Since the cycles of a permutation \(σ\) tell us \(σ(x)\) for every \(x\) in the domain of \(σ\), the cycle. Cycle decomposition of any permutation. This video demonstrates cycle notation in the symmetric group on 6 elements. F = (16325)(47)(8) the cycles can be. The cyclic decomposition of a permutation can be computed in the wolfram language with the function. Cycle Decomposition Examples.
From www.youtube.com
Cycle YouTube Cycle Decomposition Examples $\begin{pmatrix} 1 \end{pmatrix} \begin{pmatrix} 2 & 4 \end{pmatrix} \begin{pmatrix} 3 & 6 & 9. Since the cycles of a permutation \(σ\) tell us \(σ(x)\) for every \(x\) in the domain of \(σ\), the cycle. For instance, if ˇis the permutation in the previous example, we omit the cycle (3) in its disjoint cycle. Cycle decomposition of any permutation. We call. Cycle Decomposition Examples.
From demonstrations.wolfram.com
Eulerian Tour and Cycle Wolfram Demonstrations Project Cycle Decomposition Examples For instance, if ˇis the permutation in the previous example, we omit the cycle (3) in its disjoint cycle. We call the set of cycles of a permutation the cycle decomposition of the permutation. $\begin{pmatrix} 1 \end{pmatrix} \begin{pmatrix} 2 & 4 \end{pmatrix} \begin{pmatrix} 3 & 6 & 9. Cycle decomposition of any permutation. We also see a brief demonstration of. Cycle Decomposition Examples.
From groupdecompositionproject.blogspot.com
cycle of Cycle Decomposition Examples This video demonstrates cycle notation in the symmetric group on 6 elements. We call the set of cycles of a permutation the cycle decomposition of the permutation. $\begin{pmatrix} 1 \end{pmatrix} \begin{pmatrix} 2 & 4 \end{pmatrix} \begin{pmatrix} 3 & 6 & 9. F = (16325)(47)(8) the cycles can be. The cycle decomposition is f = (1,6,3,2,5)(4,7)(8) if all numbers are 1. Cycle Decomposition Examples.
From www.expii.com
Reactions — Definition & Examples Expii Cycle Decomposition Examples Since the cycles of a permutation \(σ\) tell us \(σ(x)\) for every \(x\) in the domain of \(σ\), the cycle. We call the set of cycles of a permutation the cycle decomposition of the permutation. The cycle decomposition is f = (1,6,3,2,5)(4,7)(8) if all numbers are 1 digit, we may abbreviate: The cyclic decomposition of a permutation can be computed. Cycle Decomposition Examples.
From www.researchgate.net
Figure A.1 TrendCycle United States Download Cycle Decomposition Examples Since the cycles of a permutation \(σ\) tell us \(σ(x)\) for every \(x\) in the domain of \(σ\), the cycle. We also see a brief demonstration of cycle decomposition when composing. Cycle decomposition of any permutation. The cyclic decomposition of a permutation can be computed in the wolfram language with the function permutationcycles[p]. For instance, if ˇis the permutation in. Cycle Decomposition Examples.
From www.youtube.com
[Introduction to Combinatorics] Lecture 13. Cycle of a Cycle Decomposition Examples This video demonstrates cycle notation in the symmetric group on 6 elements. We also see a brief demonstration of cycle decomposition when composing. $\begin{pmatrix} 1 \end{pmatrix} \begin{pmatrix} 2 & 4 \end{pmatrix} \begin{pmatrix} 3 & 6 & 9. The cycle decomposition for $\rho$ is: Since the cycles of a permutation \(σ\) tell us \(σ(x)\) for every \(x\) in the domain of. Cycle Decomposition Examples.
From byjus.com
Nutrient Cycle Definition, Examples and Importance Cycle Decomposition Examples This video demonstrates cycle notation in the symmetric group on 6 elements. The cycle decomposition for $\rho$ is: We also see a brief demonstration of cycle decomposition when composing. The cyclic decomposition of a permutation can be computed in the wolfram language with the function permutationcycles[p]. $\begin{pmatrix} 1 \end{pmatrix} \begin{pmatrix} 2 & 4 \end{pmatrix} \begin{pmatrix} 3 & 6 & 9.. Cycle Decomposition Examples.
From www.slideserve.com
PPT ORGANIC MATTER PowerPoint Presentation, free Cycle Decomposition Examples Cycle decomposition of any permutation. The cyclic decomposition of a permutation can be computed in the wolfram language with the function permutationcycles[p]. We call the set of cycles of a permutation the cycle decomposition of the permutation. For instance, if ˇis the permutation in the previous example, we omit the cycle (3) in its disjoint cycle. $\begin{pmatrix} 1 \end{pmatrix} \begin{pmatrix}. Cycle Decomposition Examples.
From askfilo.com
Figure 14.1 Diagrammatic representation of cycle in a terre.. Cycle Decomposition Examples The cyclic decomposition of a permutation can be computed in the wolfram language with the function permutationcycles[p]. Cycle decomposition of any permutation. F = (16325)(47)(8) the cycles can be. For instance, if ˇis the permutation in the previous example, we omit the cycle (3) in its disjoint cycle. We also see a brief demonstration of cycle decomposition when composing. This. Cycle Decomposition Examples.
From www.youtube.com
Graph Theory 26. Cycle iff All Vertices Have Even Degre Cycle Decomposition Examples Since the cycles of a permutation \(σ\) tell us \(σ(x)\) for every \(x\) in the domain of \(σ\), the cycle. F = (16325)(47)(8) the cycles can be. $\begin{pmatrix} 1 \end{pmatrix} \begin{pmatrix} 2 & 4 \end{pmatrix} \begin{pmatrix} 3 & 6 & 9. The cyclic decomposition of a permutation can be computed in the wolfram language with the function permutationcycles[p]. We also. Cycle Decomposition Examples.
From studymateriall.com
What Is Nature Of Mechanism Of Cycle Decomposition Examples The cycle decomposition for $\rho$ is: This video demonstrates cycle notation in the symmetric group on 6 elements. We call the set of cycles of a permutation the cycle decomposition of the permutation. $\begin{pmatrix} 1 \end{pmatrix} \begin{pmatrix} 2 & 4 \end{pmatrix} \begin{pmatrix} 3 & 6 & 9. Since the cycles of a permutation \(σ\) tell us \(σ(x)\) for every \(x\). Cycle Decomposition Examples.
From medium.com
The Stages of In our latest infographic, get a… by Cycle Decomposition Examples $\begin{pmatrix} 1 \end{pmatrix} \begin{pmatrix} 2 & 4 \end{pmatrix} \begin{pmatrix} 3 & 6 & 9. Cycle decomposition of any permutation. F = (16325)(47)(8) the cycles can be. We also see a brief demonstration of cycle decomposition when composing. This video demonstrates cycle notation in the symmetric group on 6 elements. The cycle decomposition is f = (1,6,3,2,5)(4,7)(8) if all numbers are. Cycle Decomposition Examples.