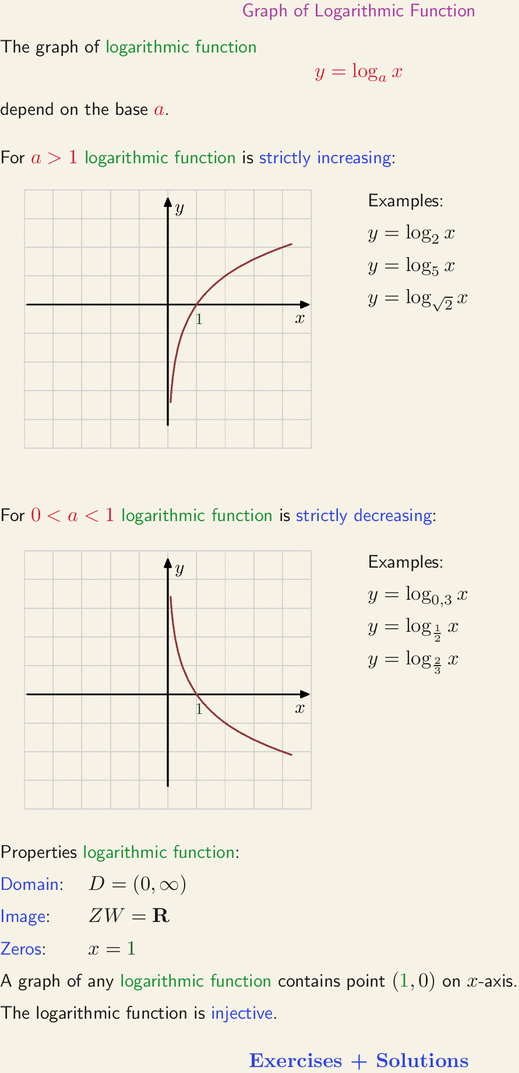
Logarithm Function Zero . The logarithmic function has the. discover the link between exponential function bⁿ = m and logₐm = n in this article about logarithms explained. the inverse logarithm (or anti logarithm) is calculated by raising the base b to the logarithm y: Properties depend on value of a this is the logarithmic function: the domain of the logarithm function with base \(b\) is \((0,\infty)\). set up an inequality showing the argument of the logarithmic function equal to zero. We give the basic properties and graphs of logarithm functions. in this section we will introduce logarithm functions. logarithmic functions with definitions of the form \(f (x) = \log_{b}x\) have a domain consisting of positive real numbers \((0, ∞)\) and a range consisting of all real numbers \((−∞, ∞)\). F(x) = log a (x) a is any value greater than 0, except 1. The range of the logarithm function with base \(b\) is \((−\infty,\infty)\). In addition, we discuss how to. Below is a graph of both f (x) = log (x) and f (x) = ln (x).
from mathinschool.com
logarithmic functions with definitions of the form \(f (x) = \log_{b}x\) have a domain consisting of positive real numbers \((0, ∞)\) and a range consisting of all real numbers \((−∞, ∞)\). F(x) = log a (x) a is any value greater than 0, except 1. In addition, we discuss how to. this is the logarithmic function: Below is a graph of both f (x) = log (x) and f (x) = ln (x). Properties depend on value of a We give the basic properties and graphs of logarithm functions. discover the link between exponential function bⁿ = m and logₐm = n in this article about logarithms explained. The range of the logarithm function with base \(b\) is \((−\infty,\infty)\). the domain of the logarithm function with base \(b\) is \((0,\infty)\).
Graph of Logarithmic Function
Logarithm Function Zero Below is a graph of both f (x) = log (x) and f (x) = ln (x). set up an inequality showing the argument of the logarithmic function equal to zero. Properties depend on value of a logarithmic functions with definitions of the form \(f (x) = \log_{b}x\) have a domain consisting of positive real numbers \((0, ∞)\) and a range consisting of all real numbers \((−∞, ∞)\). F(x) = log a (x) a is any value greater than 0, except 1. In addition, we discuss how to. The range of the logarithm function with base \(b\) is \((−\infty,\infty)\). The logarithmic function has the. Below is a graph of both f (x) = log (x) and f (x) = ln (x). in this section we will introduce logarithm functions. discover the link between exponential function bⁿ = m and logₐm = n in this article about logarithms explained. this is the logarithmic function: We give the basic properties and graphs of logarithm functions. the inverse logarithm (or anti logarithm) is calculated by raising the base b to the logarithm y: the domain of the logarithm function with base \(b\) is \((0,\infty)\).
From courses.lumenlearning.com
Graphs of Logarithmic Functions Algebra and Trigonometry Logarithm Function Zero set up an inequality showing the argument of the logarithmic function equal to zero. this is the logarithmic function: in this section we will introduce logarithm functions. We give the basic properties and graphs of logarithm functions. discover the link between exponential function bⁿ = m and logₐm = n in this article about logarithms explained.. Logarithm Function Zero.
From www.onlinemath4all.com
Domain and Range of Logarithmic Functions Logarithm Function Zero set up an inequality showing the argument of the logarithmic function equal to zero. F(x) = log a (x) a is any value greater than 0, except 1. discover the link between exponential function bⁿ = m and logₐm = n in this article about logarithms explained. in this section we will introduce logarithm functions. logarithmic. Logarithm Function Zero.
From www.geogebra.org
Logarithmic Functions with Bases Between Zero and One GeoGebra Logarithm Function Zero The range of the logarithm function with base \(b\) is \((−\infty,\infty)\). the inverse logarithm (or anti logarithm) is calculated by raising the base b to the logarithm y: logarithmic functions with definitions of the form \(f (x) = \log_{b}x\) have a domain consisting of positive real numbers \((0, ∞)\) and a range consisting of all real numbers \((−∞,. Logarithm Function Zero.
From cejbochk.blob.core.windows.net
Logarithmic Equation at Hannah Cook blog Logarithm Function Zero F(x) = log a (x) a is any value greater than 0, except 1. the inverse logarithm (or anti logarithm) is calculated by raising the base b to the logarithm y: set up an inequality showing the argument of the logarithmic function equal to zero. The range of the logarithm function with base \(b\) is \((−\infty,\infty)\). in. Logarithm Function Zero.
From www.ck12.org
Logarithmic Functions CK12 Foundation Logarithm Function Zero The logarithmic function has the. in this section we will introduce logarithm functions. F(x) = log a (x) a is any value greater than 0, except 1. In addition, we discuss how to. We give the basic properties and graphs of logarithm functions. this is the logarithmic function: discover the link between exponential function bⁿ = m. Logarithm Function Zero.
From helpingwithmath.com
Logarithms What?, Importance, Properties, Expressions Logarithm Function Zero Properties depend on value of a in this section we will introduce logarithm functions. The range of the logarithm function with base \(b\) is \((−\infty,\infty)\). discover the link between exponential function bⁿ = m and logₐm = n in this article about logarithms explained. the inverse logarithm (or anti logarithm) is calculated by raising the base b. Logarithm Function Zero.
From www.youtube.com
Find Zeros of Exponential and Logarithmic Equations YouTube Logarithm Function Zero the domain of the logarithm function with base \(b\) is \((0,\infty)\). F(x) = log a (x) a is any value greater than 0, except 1. In addition, we discuss how to. Properties depend on value of a this is the logarithmic function: discover the link between exponential function bⁿ = m and logₐm = n in this. Logarithm Function Zero.
From printablestojanki.z4.web.core.windows.net
All Rules Of Logarithms Logarithm Function Zero The logarithmic function has the. Below is a graph of both f (x) = log (x) and f (x) = ln (x). We give the basic properties and graphs of logarithm functions. discover the link between exponential function bⁿ = m and logₐm = n in this article about logarithms explained. In addition, we discuss how to. Properties depend. Logarithm Function Zero.
From mathsathome.com
Logarithm Laws Made Easy A Complete Guide with Examples Logarithm Function Zero set up an inequality showing the argument of the logarithmic function equal to zero. logarithmic functions with definitions of the form \(f (x) = \log_{b}x\) have a domain consisting of positive real numbers \((0, ∞)\) and a range consisting of all real numbers \((−∞, ∞)\). The logarithmic function has the. discover the link between exponential function bⁿ. Logarithm Function Zero.
From www.slideserve.com
PPT Logarithmic Functions PowerPoint Presentation, free download ID Logarithm Function Zero Below is a graph of both f (x) = log (x) and f (x) = ln (x). F(x) = log a (x) a is any value greater than 0, except 1. In addition, we discuss how to. The range of the logarithm function with base \(b\) is \((−\infty,\infty)\). the inverse logarithm (or anti logarithm) is calculated by raising the. Logarithm Function Zero.
From learningschoolenrichifa.z22.web.core.windows.net
Rules Of Logarithms With Examples Logarithm Function Zero in this section we will introduce logarithm functions. the inverse logarithm (or anti logarithm) is calculated by raising the base b to the logarithm y: The logarithmic function has the. the domain of the logarithm function with base \(b\) is \((0,\infty)\). discover the link between exponential function bⁿ = m and logₐm = n in this. Logarithm Function Zero.
From brilliant.org
Applying Differentiation Rules To Logarithmic Functions Brilliant Logarithm Function Zero in this section we will introduce logarithm functions. discover the link between exponential function bⁿ = m and logₐm = n in this article about logarithms explained. F(x) = log a (x) a is any value greater than 0, except 1. this is the logarithmic function: logarithmic functions with definitions of the form \(f (x) =. Logarithm Function Zero.
From printablestojanki.z4.web.core.windows.net
Basic Rules Of Logarithms Logarithm Function Zero The range of the logarithm function with base \(b\) is \((−\infty,\infty)\). the inverse logarithm (or anti logarithm) is calculated by raising the base b to the logarithm y: We give the basic properties and graphs of logarithm functions. F(x) = log a (x) a is any value greater than 0, except 1. discover the link between exponential function. Logarithm Function Zero.
From courses.lumenlearning.com
Graphs of Exponential and Logarithmic Functions Boundless Algebra Logarithm Function Zero logarithmic functions with definitions of the form \(f (x) = \log_{b}x\) have a domain consisting of positive real numbers \((0, ∞)\) and a range consisting of all real numbers \((−∞, ∞)\). in this section we will introduce logarithm functions. Below is a graph of both f (x) = log (x) and f (x) = ln (x). Properties depend. Logarithm Function Zero.
From materialschoolpinder.z21.web.core.windows.net
Solving A Logarithmic Equation Logarithm Function Zero discover the link between exponential function bⁿ = m and logₐm = n in this article about logarithms explained. in this section we will introduce logarithm functions. set up an inequality showing the argument of the logarithmic function equal to zero. We give the basic properties and graphs of logarithm functions. logarithmic functions with definitions of. Logarithm Function Zero.
From dishcuss.com
Logarithmic Cheat Sheet photos and vectors Logarithm Function Zero discover the link between exponential function bⁿ = m and logₐm = n in this article about logarithms explained. set up an inequality showing the argument of the logarithmic function equal to zero. The range of the logarithm function with base \(b\) is \((−\infty,\infty)\). logarithmic functions with definitions of the form \(f (x) = \log_{b}x\) have a. Logarithm Function Zero.
From www.sfu.ca
Logarithmic Functions Logarithm Function Zero In addition, we discuss how to. the domain of the logarithm function with base \(b\) is \((0,\infty)\). logarithmic functions with definitions of the form \(f (x) = \log_{b}x\) have a domain consisting of positive real numbers \((0, ∞)\) and a range consisting of all real numbers \((−∞, ∞)\). Properties depend on value of a this is the. Logarithm Function Zero.
From www.scribd.com
Express The Intercept and Zeros of Logarithmic Function Using Set Logarithm Function Zero the domain of the logarithm function with base \(b\) is \((0,\infty)\). set up an inequality showing the argument of the logarithmic function equal to zero. The logarithmic function has the. F(x) = log a (x) a is any value greater than 0, except 1. the inverse logarithm (or anti logarithm) is calculated by raising the base b. Logarithm Function Zero.
From slideplayer.com
Logarithmic Functions ppt download Logarithm Function Zero F(x) = log a (x) a is any value greater than 0, except 1. Below is a graph of both f (x) = log (x) and f (x) = ln (x). discover the link between exponential function bⁿ = m and logₐm = n in this article about logarithms explained. the inverse logarithm (or anti logarithm) is calculated. Logarithm Function Zero.
From mathinschool.com
Graph of Logarithmic Function Logarithm Function Zero discover the link between exponential function bⁿ = m and logₐm = n in this article about logarithms explained. the domain of the logarithm function with base \(b\) is \((0,\infty)\). The logarithmic function has the. Properties depend on value of a logarithmic functions with definitions of the form \(f (x) = \log_{b}x\) have a domain consisting of. Logarithm Function Zero.
From dybffzwseco.blob.core.windows.net
Logarithms Domain at Ruth Wilson blog Logarithm Function Zero the domain of the logarithm function with base \(b\) is \((0,\infty)\). Properties depend on value of a The logarithmic function has the. We give the basic properties and graphs of logarithm functions. set up an inequality showing the argument of the logarithmic function equal to zero. Below is a graph of both f (x) = log (x) and. Logarithm Function Zero.
From www.youtube.com
Find Minimum Number of Zeros for Logarithmic Function YouTube Logarithm Function Zero In addition, we discuss how to. discover the link between exponential function bⁿ = m and logₐm = n in this article about logarithms explained. the domain of the logarithm function with base \(b\) is \((0,\infty)\). set up an inequality showing the argument of the logarithmic function equal to zero. Below is a graph of both f. Logarithm Function Zero.
From www.cuemath.com
Logarithmic Functions Formula, Domain, Range, Graph Logarithm Function Zero Below is a graph of both f (x) = log (x) and f (x) = ln (x). F(x) = log a (x) a is any value greater than 0, except 1. Properties depend on value of a the domain of the logarithm function with base \(b\) is \((0,\infty)\). The range of the logarithm function with base \(b\) is \((−\infty,\infty)\).. Logarithm Function Zero.
From studyfullnatasha.z21.web.core.windows.net
Rules Of Logarithmic Functions Logarithm Function Zero Properties depend on value of a discover the link between exponential function bⁿ = m and logₐm = n in this article about logarithms explained. The logarithmic function has the. the domain of the logarithm function with base \(b\) is \((0,\infty)\). F(x) = log a (x) a is any value greater than 0, except 1. in this. Logarithm Function Zero.
From en.wikipedia.org
Logarithm Wikipedia Logarithm Function Zero discover the link between exponential function bⁿ = m and logₐm = n in this article about logarithms explained. in this section we will introduce logarithm functions. set up an inequality showing the argument of the logarithmic function equal to zero. F(x) = log a (x) a is any value greater than 0, except 1. In addition,. Logarithm Function Zero.
From www.youtube.com
Find the domain, intercepts, asymptotes of a logarithmic function YouTube Logarithm Function Zero F(x) = log a (x) a is any value greater than 0, except 1. discover the link between exponential function bⁿ = m and logₐm = n in this article about logarithms explained. Properties depend on value of a logarithmic functions with definitions of the form \(f (x) = \log_{b}x\) have a domain consisting of positive real numbers. Logarithm Function Zero.
From courses.lumenlearning.com
Graphs of Logarithmic Functions College Algebra Logarithm Function Zero set up an inequality showing the argument of the logarithmic function equal to zero. this is the logarithmic function: discover the link between exponential function bⁿ = m and logₐm = n in this article about logarithms explained. Below is a graph of both f (x) = log (x) and f (x) = ln (x). The range. Logarithm Function Zero.
From www.cuemath.com
Logarithm Introduction What is Logarithm, Rules, Functions Logarithm Function Zero The range of the logarithm function with base \(b\) is \((−\infty,\infty)\). logarithmic functions with definitions of the form \(f (x) = \log_{b}x\) have a domain consisting of positive real numbers \((0, ∞)\) and a range consisting of all real numbers \((−∞, ∞)\). F(x) = log a (x) a is any value greater than 0, except 1. the domain. Logarithm Function Zero.
From www.slideserve.com
PPT Finding Zeros of Polynomials PowerPoint Presentation, free Logarithm Function Zero set up an inequality showing the argument of the logarithmic function equal to zero. in this section we will introduce logarithm functions. discover the link between exponential function bⁿ = m and logₐm = n in this article about logarithms explained. The logarithmic function has the. logarithmic functions with definitions of the form \(f (x) =. Logarithm Function Zero.
From courses.lumenlearning.com
Graphs of Logarithmic Functions Algebra and Trigonometry Logarithm Function Zero the domain of the logarithm function with base \(b\) is \((0,\infty)\). F(x) = log a (x) a is any value greater than 0, except 1. logarithmic functions with definitions of the form \(f (x) = \log_{b}x\) have a domain consisting of positive real numbers \((0, ∞)\) and a range consisting of all real numbers \((−∞, ∞)\). Properties depend. Logarithm Function Zero.
From philschatz.com
Graphs of Logarithmic Functions · Precalculus Logarithm Function Zero the domain of the logarithm function with base \(b\) is \((0,\infty)\). logarithmic functions with definitions of the form \(f (x) = \log_{b}x\) have a domain consisting of positive real numbers \((0, ∞)\) and a range consisting of all real numbers \((−∞, ∞)\). in this section we will introduce logarithm functions. We give the basic properties and graphs. Logarithm Function Zero.
From mathodics.com
Understanding the Properties of Log Functions Logarithm Function Zero this is the logarithmic function: We give the basic properties and graphs of logarithm functions. F(x) = log a (x) a is any value greater than 0, except 1. set up an inequality showing the argument of the logarithmic function equal to zero. the inverse logarithm (or anti logarithm) is calculated by raising the base b to. Logarithm Function Zero.
From physicscatalyst.com
Logarithm functions Graph,Properties, Derivatives, Solved Examples Logarithm Function Zero the inverse logarithm (or anti logarithm) is calculated by raising the base b to the logarithm y: Properties depend on value of a in this section we will introduce logarithm functions. set up an inequality showing the argument of the logarithmic function equal to zero. logarithmic functions with definitions of the form \(f (x) = \log_{b}x\). Logarithm Function Zero.
From mathvault.ca
Logarithm The Complete Guide (Theory & Applications) Math Vault Logarithm Function Zero the inverse logarithm (or anti logarithm) is calculated by raising the base b to the logarithm y: Properties depend on value of a the domain of the logarithm function with base \(b\) is \((0,\infty)\). Below is a graph of both f (x) = log (x) and f (x) = ln (x). F(x) = log a (x) a is. Logarithm Function Zero.
From flamath.com
Limits of Logarithmic Functions at Point and Infinity Logarithm Function Zero in this section we will introduce logarithm functions. the inverse logarithm (or anti logarithm) is calculated by raising the base b to the logarithm y: Properties depend on value of a discover the link between exponential function bⁿ = m and logₐm = n in this article about logarithms explained. In addition, we discuss how to. Below. Logarithm Function Zero.