Pendant Vertex at Raymond Irwin blog

Pendant Vertex. Let g g be a graph. A vertex v v of g g is said to be a pendant vertex if and only if it has degree 1 1. Prove that the number of pendant vertices. Vtnr plummeted more than 58% on wednesday after the producer and. the pendant number of a graph g, denoted by \(\varpi _p(g)\), is the least number of vertices in the graph \( g. A vertex having no incident edge is called an isolated vertex. , v_n \}$ for $n \geq 2$. For a graph g = (v(g), e(g)), a vertex x1 ∈ v(g) is. a vertex u is called a pendant vertex (or a leaf) of g if d g ( u) = 1. although \(g_1\) and \(g_2\) use the same names for the vertices, they apply to different vertices in the graph: a vertex whose removal in a graph g increases the number of components of g is called a cut vertex. The number of edges incident on a vertex. Shares of vertex energy, inc. a vertex of a graph is said to be pendant if its neighborhood contains exactly one vertex. a vertex of degree one is called a pendant vertex, and the edge incident to it is a pendant edge.

Deg (v) =1 • isolated vertex: the pendant number of a graph g, denoted by \(\varpi _p(g)\), is the least number of vertices in the graph \( g. Let g g be a graph. In a graph, pendant vertices are the vertices that have a degree of 1, meaning they are connected. a tree on 1 vertex has 0 edges; we are essentially dividing a vertex in two, thus there are $|v|=4+5+3+1+\color{red}{1}+p=14+p$. This is the base case. , v_n \}$ for $n \geq 2$. The unique neighbor of a pendant vertex is. a vertex whose removal in a graph g increases the number of components of g is called a cut vertex.

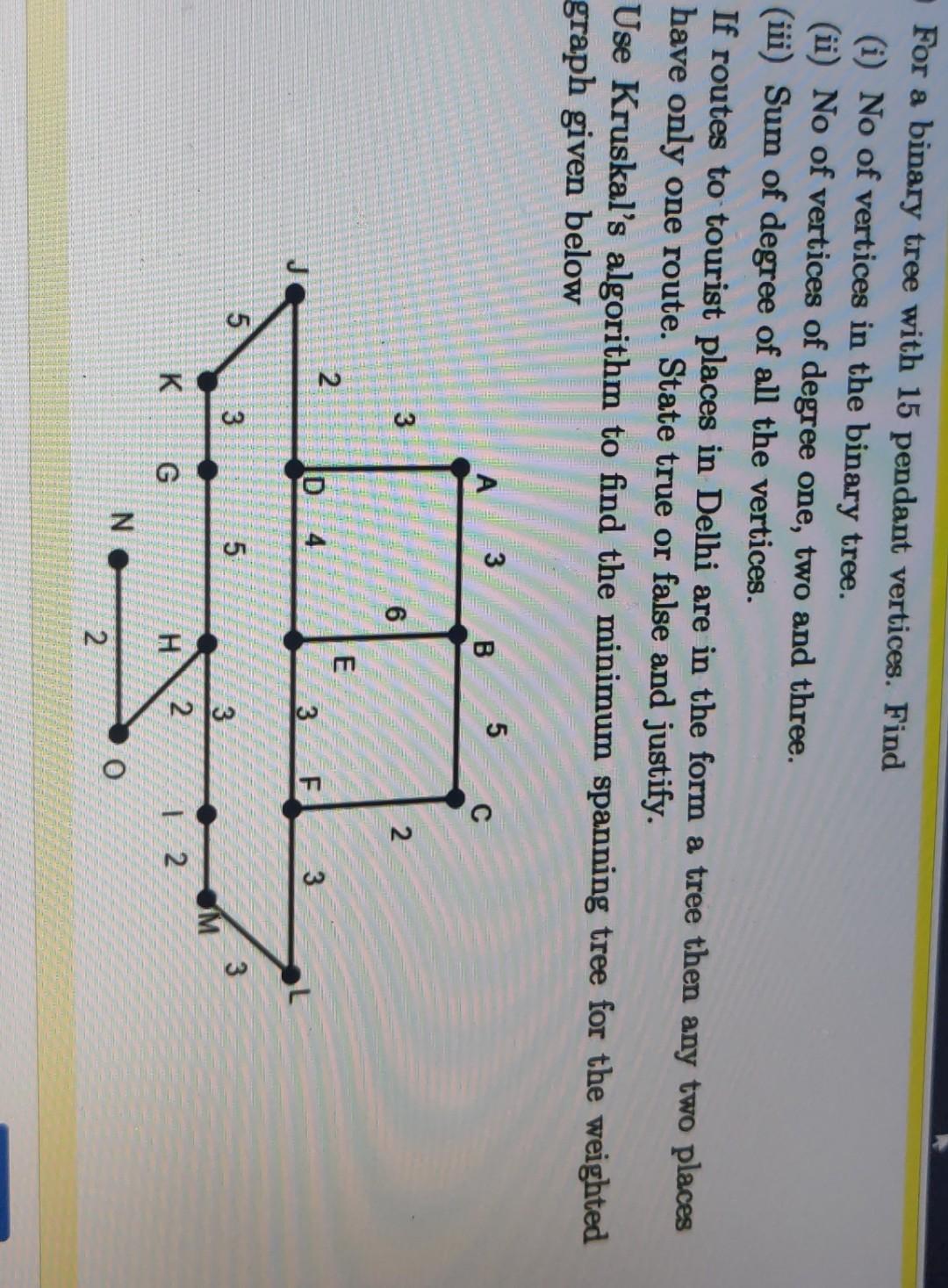
Solved For a binary tree with 15 pendant vertices. Find (i)

Pendant Vertex , v_n \}$ for $n \geq 2$. For a graph g = (v(g), e(g)), a vertex x1 ∈ v(g) is. Shares of vertex energy, inc. Vtnr plummeted more than 58% on wednesday after the producer and. Prove that the number of pendant vertices. A vertex having no incident edge is called an isolated vertex. a vertex with degree 1 is called a leaf vertex or end vertex or a pendant vertex, and the edge incident with that vertex is called a. a vertex u is called a pendant vertex (or a leaf) of g if d g ( u) = 1. let $t$ be a tree with vertices $\{v_1, v_2,. although \(g_1\) and \(g_2\) use the same names for the vertices, they apply to different vertices in the graph: we are essentially dividing a vertex in two, thus there are $|v|=4+5+3+1+\color{red}{1}+p=14+p$. A vertex v v of g g is said to be a pendant vertex if and only if it has degree 1 1. The number of edges incident on a vertex. the pendant number of a graph g, denoted by \(\varpi _p(g)\), is the least number of vertices in the graph \( g. Let g g be a graph. Let g be a graph, a vertex v of g is called a pendant vertex if and only if v has degree 1.