Cross Edge Dfs . It is an edge that connects two nodes such that they do not have any ancestor and a descendant relationship between them. That is, $(u,v) \in e'$ is a forward edge if $u$ is an. Else, if v is neither an ancestor or descendant of u, then edge (u; A cross edge in a graph is an edge that goes from a vertex $v$ to another vertex $u$ such that $u$ is neither an ancestor nor descendant of $v$. Backtrack along breadcrumbs until reach unexplored neighbor. So what you need to argue is that in an. Follow path until you get stuck. Cross edges point from one vertex to another vertex to which it is incomparable with respect to the ordering induced by the dfs tree. V) is a forward edge. Else, if v is a descendant of u, then edge (u;
from www.chegg.com
Cross edges point from one vertex to another vertex to which it is incomparable with respect to the ordering induced by the dfs tree. A cross edge in a graph is an edge that goes from a vertex $v$ to another vertex $u$ such that $u$ is neither an ancestor nor descendant of $v$. V) is a forward edge. Else, if v is a descendant of u, then edge (u; That is, $(u,v) \in e'$ is a forward edge if $u$ is an. Follow path until you get stuck. Backtrack along breadcrumbs until reach unexplored neighbor. It is an edge that connects two nodes such that they do not have any ancestor and a descendant relationship between them. Else, if v is neither an ancestor or descendant of u, then edge (u; So what you need to argue is that in an.
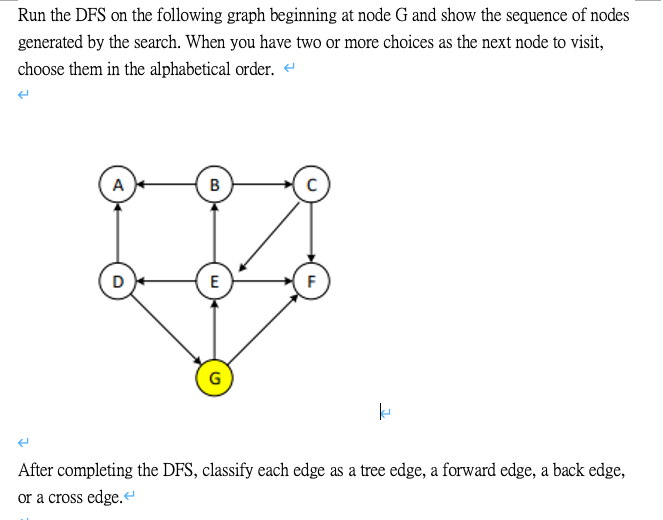
Solved Run the DFS on the following graph beginning at node
Cross Edge Dfs Follow path until you get stuck. Follow path until you get stuck. That is, $(u,v) \in e'$ is a forward edge if $u$ is an. Else, if v is a descendant of u, then edge (u; Else, if v is neither an ancestor or descendant of u, then edge (u; A cross edge in a graph is an edge that goes from a vertex $v$ to another vertex $u$ such that $u$ is neither an ancestor nor descendant of $v$. Backtrack along breadcrumbs until reach unexplored neighbor. So what you need to argue is that in an. V) is a forward edge. Cross edges point from one vertex to another vertex to which it is incomparable with respect to the ordering induced by the dfs tree. It is an edge that connects two nodes such that they do not have any ancestor and a descendant relationship between them.
From www.interviewbit.com
Depth First Search InterviewBit Cross Edge Dfs So what you need to argue is that in an. Follow path until you get stuck. Backtrack along breadcrumbs until reach unexplored neighbor. Cross edges point from one vertex to another vertex to which it is incomparable with respect to the ordering induced by the dfs tree. V) is a forward edge. It is an edge that connects two nodes. Cross Edge Dfs.
From www.gamingnexus.com
Cross Edge Review Gaming Nexus Cross Edge Dfs That is, $(u,v) \in e'$ is a forward edge if $u$ is an. It is an edge that connects two nodes such that they do not have any ancestor and a descendant relationship between them. So what you need to argue is that in an. Else, if v is neither an ancestor or descendant of u, then edge (u; Else,. Cross Edge Dfs.
From www.legendra.com
Cross Edge Fiche RPG (reviews, previews, wallpapers, videos, covers Cross Edge Dfs Else, if v is neither an ancestor or descendant of u, then edge (u; V) is a forward edge. Backtrack along breadcrumbs until reach unexplored neighbor. A cross edge in a graph is an edge that goes from a vertex $v$ to another vertex $u$ such that $u$ is neither an ancestor nor descendant of $v$. Cross edges point from. Cross Edge Dfs.
From www.slideserve.com
PPT 20. DFS, BFS, Biconnectivity, Digraphs PowerPoint Presentation Cross Edge Dfs Cross edges point from one vertex to another vertex to which it is incomparable with respect to the ordering induced by the dfs tree. A cross edge in a graph is an edge that goes from a vertex $v$ to another vertex $u$ such that $u$ is neither an ancestor nor descendant of $v$. So what you need to argue. Cross Edge Dfs.
From www.giantbomb.com
Cross Edge International Releases Giant Bomb Cross Edge Dfs So what you need to argue is that in an. That is, $(u,v) \in e'$ is a forward edge if $u$ is an. V) is a forward edge. Else, if v is neither an ancestor or descendant of u, then edge (u; It is an edge that connects two nodes such that they do not have any ancestor and a. Cross Edge Dfs.
From www.youtube.com
Ch 2.7 DFS depthfirst forest ,Tree edges , Back edges ,Forward edges Cross Edge Dfs Cross edges point from one vertex to another vertex to which it is incomparable with respect to the ordering induced by the dfs tree. That is, $(u,v) \in e'$ is a forward edge if $u$ is an. Backtrack along breadcrumbs until reach unexplored neighbor. Else, if v is neither an ancestor or descendant of u, then edge (u; A cross. Cross Edge Dfs.
From www.codeforces.com
[Tutorial] The DFS tree and its applications how I found out I really Cross Edge Dfs V) is a forward edge. It is an edge that connects two nodes such that they do not have any ancestor and a descendant relationship between them. So what you need to argue is that in an. Cross edges point from one vertex to another vertex to which it is incomparable with respect to the ordering induced by the dfs. Cross Edge Dfs.
From www.gematsu.com
Cross Edge Review Gematsu Cross Edge Dfs So what you need to argue is that in an. V) is a forward edge. It is an edge that connects two nodes such that they do not have any ancestor and a descendant relationship between them. Else, if v is neither an ancestor or descendant of u, then edge (u; Follow path until you get stuck. Backtrack along breadcrumbs. Cross Edge Dfs.
From slideplayer.com
Graph Algorithms Using Depth First Search ppt download Cross Edge Dfs Else, if v is a descendant of u, then edge (u; Cross edges point from one vertex to another vertex to which it is incomparable with respect to the ordering induced by the dfs tree. Else, if v is neither an ancestor or descendant of u, then edge (u; A cross edge in a graph is an edge that goes. Cross Edge Dfs.
From rpgamer.com
Cross Edge Review RPGamer Cross Edge Dfs Backtrack along breadcrumbs until reach unexplored neighbor. V) is a forward edge. It is an edge that connects two nodes such that they do not have any ancestor and a descendant relationship between them. Follow path until you get stuck. A cross edge in a graph is an edge that goes from a vertex $v$ to another vertex $u$ such. Cross Edge Dfs.
From steam-games.org
Cross Edge Steam Games Cross Edge Dfs Else, if v is a descendant of u, then edge (u; Else, if v is neither an ancestor or descendant of u, then edge (u; So what you need to argue is that in an. It is an edge that connects two nodes such that they do not have any ancestor and a descendant relationship between them. That is, $(u,v). Cross Edge Dfs.
From studylib.net
DFS Edge Classification Cross Edge Dfs Follow path until you get stuck. A cross edge in a graph is an edge that goes from a vertex $v$ to another vertex $u$ such that $u$ is neither an ancestor nor descendant of $v$. Backtrack along breadcrumbs until reach unexplored neighbor. Else, if v is a descendant of u, then edge (u; V) is a forward edge. Cross. Cross Edge Dfs.
From www.ign.com
Cross Edge IGN Cross Edge Dfs That is, $(u,v) \in e'$ is a forward edge if $u$ is an. Cross edges point from one vertex to another vertex to which it is incomparable with respect to the ordering induced by the dfs tree. Else, if v is a descendant of u, then edge (u; Follow path until you get stuck. Else, if v is neither an. Cross Edge Dfs.
From www.gamingnexus.com
Cross Edge Review Gaming Nexus Cross Edge Dfs Backtrack along breadcrumbs until reach unexplored neighbor. It is an edge that connects two nodes such that they do not have any ancestor and a descendant relationship between them. Else, if v is neither an ancestor or descendant of u, then edge (u; V) is a forward edge. That is, $(u,v) \in e'$ is a forward edge if $u$ is. Cross Edge Dfs.
From www.slideserve.com
PPT Advanced DFS, BFS, Graph Modeling PowerPoint Presentation, free Cross Edge Dfs Cross edges point from one vertex to another vertex to which it is incomparable with respect to the ordering induced by the dfs tree. Else, if v is neither an ancestor or descendant of u, then edge (u; Else, if v is a descendant of u, then edge (u; So what you need to argue is that in an. Follow. Cross Edge Dfs.
From pics.alphacoders.com
Cross Edge Picture Image Abyss Cross Edge Dfs It is an edge that connects two nodes such that they do not have any ancestor and a descendant relationship between them. Follow path until you get stuck. Backtrack along breadcrumbs until reach unexplored neighbor. So what you need to argue is that in an. Else, if v is neither an ancestor or descendant of u, then edge (u; Cross. Cross Edge Dfs.
From www.youtube.com
6.3 Types of Edges in DFS Edge Classification Data Structures and Cross Edge Dfs Follow path until you get stuck. It is an edge that connects two nodes such that they do not have any ancestor and a descendant relationship between them. Cross edges point from one vertex to another vertex to which it is incomparable with respect to the ordering induced by the dfs tree. That is, $(u,v) \in e'$ is a forward. Cross Edge Dfs.
From www.chegg.com
Solved Run the DFS on the following graph beginning at node Cross Edge Dfs That is, $(u,v) \in e'$ is a forward edge if $u$ is an. Backtrack along breadcrumbs until reach unexplored neighbor. Follow path until you get stuck. A cross edge in a graph is an edge that goes from a vertex $v$ to another vertex $u$ such that $u$ is neither an ancestor nor descendant of $v$. V) is a forward. Cross Edge Dfs.
From www.vgchartz.com
Cross Edge for PlayStation 3 Sales, Wiki, Release Dates, Review Cross Edge Dfs Cross edges point from one vertex to another vertex to which it is incomparable with respect to the ordering induced by the dfs tree. Else, if v is a descendant of u, then edge (u; Else, if v is neither an ancestor or descendant of u, then edge (u; V) is a forward edge. Follow path until you get stuck.. Cross Edge Dfs.
From slideplayer.com
Data Structures & Algorithms Digraphs and DAGs ppt download Cross Edge Dfs Cross edges point from one vertex to another vertex to which it is incomparable with respect to the ordering induced by the dfs tree. Else, if v is a descendant of u, then edge (u; A cross edge in a graph is an edge that goes from a vertex $v$ to another vertex $u$ such that $u$ is neither an. Cross Edge Dfs.
From www.geeksforgeeks.org
Tree, Back, Edge and Cross Edges in DFS of Graph Cross Edge Dfs A cross edge in a graph is an edge that goes from a vertex $v$ to another vertex $u$ such that $u$ is neither an ancestor nor descendant of $v$. Follow path until you get stuck. It is an edge that connects two nodes such that they do not have any ancestor and a descendant relationship between them. Else, if. Cross Edge Dfs.
From capcom.fandom.com
Cross Edge Database FANDOM powered by Wikia Cross Edge Dfs Follow path until you get stuck. Else, if v is a descendant of u, then edge (u; So what you need to argue is that in an. Backtrack along breadcrumbs until reach unexplored neighbor. V) is a forward edge. That is, $(u,v) \in e'$ is a forward edge if $u$ is an. It is an edge that connects two nodes. Cross Edge Dfs.
From www.gamingnexus.com
Cross Edge Review Gaming Nexus Cross Edge Dfs Else, if v is a descendant of u, then edge (u; V) is a forward edge. It is an edge that connects two nodes such that they do not have any ancestor and a descendant relationship between them. A cross edge in a graph is an edge that goes from a vertex $v$ to another vertex $u$ such that $u$. Cross Edge Dfs.
From www.chegg.com
In the pseudocode description of the directed DFS Cross Edge Dfs That is, $(u,v) \in e'$ is a forward edge if $u$ is an. It is an edge that connects two nodes such that they do not have any ancestor and a descendant relationship between them. Else, if v is neither an ancestor or descendant of u, then edge (u; V) is a forward edge. Follow path until you get stuck.. Cross Edge Dfs.
From www.slideserve.com
PPT DepthFirst Search PowerPoint Presentation, free download ID Cross Edge Dfs V) is a forward edge. Else, if v is neither an ancestor or descendant of u, then edge (u; Cross edges point from one vertex to another vertex to which it is incomparable with respect to the ordering induced by the dfs tree. A cross edge in a graph is an edge that goes from a vertex $v$ to another. Cross Edge Dfs.
From www.youtube.com
「Cross Edge (XEdge)」 Post Game Final Boss ☆Doppelganger☆ (1080p) YouTube Cross Edge Dfs So what you need to argue is that in an. A cross edge in a graph is an edge that goes from a vertex $v$ to another vertex $u$ such that $u$ is neither an ancestor nor descendant of $v$. Else, if v is a descendant of u, then edge (u; Backtrack along breadcrumbs until reach unexplored neighbor. Follow path. Cross Edge Dfs.
From www.youtube.com
Types of Edges in Dfs tree Graph Detailed explanation Harshit jain Cross Edge Dfs V) is a forward edge. A cross edge in a graph is an edge that goes from a vertex $v$ to another vertex $u$ such that $u$ is neither an ancestor nor descendant of $v$. So what you need to argue is that in an. It is an edge that connects two nodes such that they do not have any. Cross Edge Dfs.
From www.youtube.com
DFS and Its Applications and ALL TRICKY GATE PYQs Revision and Cross Edge Dfs Else, if v is a descendant of u, then edge (u; Follow path until you get stuck. V) is a forward edge. So what you need to argue is that in an. It is an edge that connects two nodes such that they do not have any ancestor and a descendant relationship between them. Backtrack along breadcrumbs until reach unexplored. Cross Edge Dfs.
From rpgamer.com
Cross Edge Review RPGamer Cross Edge Dfs That is, $(u,v) \in e'$ is a forward edge if $u$ is an. It is an edge that connects two nodes such that they do not have any ancestor and a descendant relationship between them. Backtrack along breadcrumbs until reach unexplored neighbor. V) is a forward edge. Else, if v is neither an ancestor or descendant of u, then edge. Cross Edge Dfs.
From www.slideserve.com
PPT DepthFirst Search PowerPoint Presentation, free download ID Cross Edge Dfs A cross edge in a graph is an edge that goes from a vertex $v$ to another vertex $u$ such that $u$ is neither an ancestor nor descendant of $v$. So what you need to argue is that in an. V) is a forward edge. Follow path until you get stuck. It is an edge that connects two nodes such. Cross Edge Dfs.
From www.zonared.com
Cross Edge todo sobre el juego, en Zonared Cross Edge Dfs Else, if v is a descendant of u, then edge (u; V) is a forward edge. Cross edges point from one vertex to another vertex to which it is incomparable with respect to the ordering induced by the dfs tree. It is an edge that connects two nodes such that they do not have any ancestor and a descendant relationship. Cross Edge Dfs.
From www.youtube.com
DFS and Its Applications and ALL TRICKY GATE PYQs Revision and Cross Edge Dfs That is, $(u,v) \in e'$ is a forward edge if $u$ is an. Backtrack along breadcrumbs until reach unexplored neighbor. A cross edge in a graph is an edge that goes from a vertex $v$ to another vertex $u$ such that $u$ is neither an ancestor nor descendant of $v$. It is an edge that connects two nodes such that. Cross Edge Dfs.
From www.slideserve.com
PPT Graph Undirected graph Directed graph PowerPoint Presentation Cross Edge Dfs Follow path until you get stuck. A cross edge in a graph is an edge that goes from a vertex $v$ to another vertex $u$ such that $u$ is neither an ancestor nor descendant of $v$. It is an edge that connects two nodes such that they do not have any ancestor and a descendant relationship between them. Else, if. Cross Edge Dfs.
From www.youtube.com
Cross Edge (PS3) Gameplay YouTube Cross Edge Dfs Backtrack along breadcrumbs until reach unexplored neighbor. That is, $(u,v) \in e'$ is a forward edge if $u$ is an. Follow path until you get stuck. Cross edges point from one vertex to another vertex to which it is incomparable with respect to the ordering induced by the dfs tree. So what you need to argue is that in an.. Cross Edge Dfs.
From www.slideserve.com
PPT Graph Undirected graph Directed graph PowerPoint Presentation Cross Edge Dfs Else, if v is neither an ancestor or descendant of u, then edge (u; Else, if v is a descendant of u, then edge (u; Cross edges point from one vertex to another vertex to which it is incomparable with respect to the ordering induced by the dfs tree. Backtrack along breadcrumbs until reach unexplored neighbor. Follow path until you. Cross Edge Dfs.