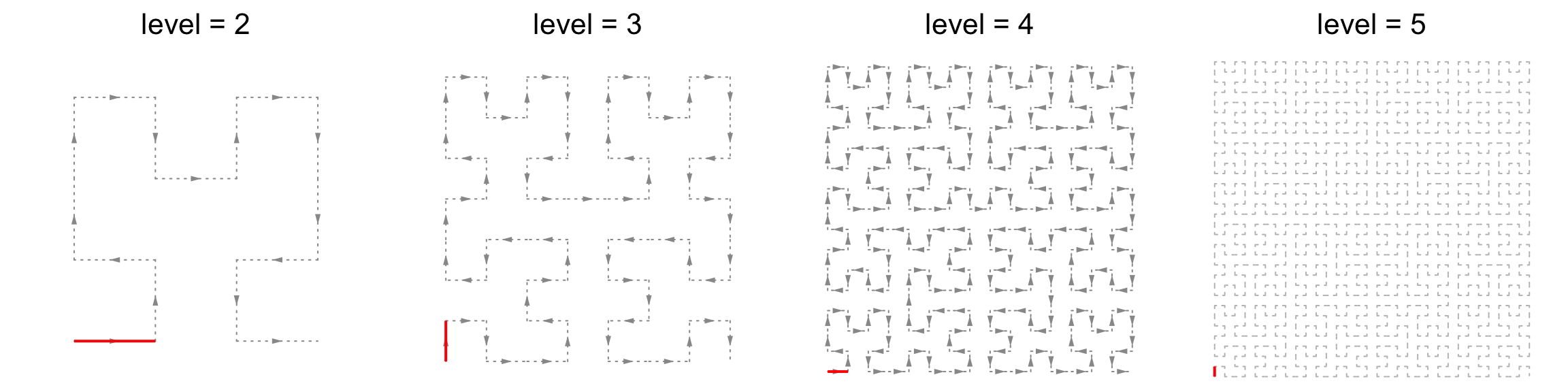
Hilbert Curve Properties . 1) the sequence {fn} converges uniformly; The function jn is a root of n(j; The hilbert curve has always bugged me because it had no closed equation or function that i could find. 2) the limit function touches every point in the square. To prove 1), we note that in the interval [k4 − n, (k + 1)4 − n),. If we take a curve like the one. The two claims to be proven are: A nice description of hilbert curves can be seen in grant sanderson’s (. What is its equation or function? For example, if i wanted to find the. This follows from the existence of the dual isogeny. The hilbert curve is a remarkable construct in many ways, but the thing that makes it useful in computer science is the fact that it has good clustering properties.
from jokergoo.github.io
1) the sequence {fn} converges uniformly; 2) the limit function touches every point in the square. For example, if i wanted to find the. The function jn is a root of n(j; If we take a curve like the one. A nice description of hilbert curves can be seen in grant sanderson’s (. This follows from the existence of the dual isogeny. What is its equation or function? The two claims to be proven are: The hilbert curve has always bugged me because it had no closed equation or function that i could find.
HilbertCurve
Hilbert Curve Properties For example, if i wanted to find the. A nice description of hilbert curves can be seen in grant sanderson’s (. What is its equation or function? The hilbert curve has always bugged me because it had no closed equation or function that i could find. If we take a curve like the one. The hilbert curve is a remarkable construct in many ways, but the thing that makes it useful in computer science is the fact that it has good clustering properties. 2) the limit function touches every point in the square. This follows from the existence of the dual isogeny. The function jn is a root of n(j; For example, if i wanted to find the. The two claims to be proven are: 1) the sequence {fn} converges uniformly; To prove 1), we note that in the interval [k4 − n, (k + 1)4 − n),.
From jokergoo.github.io
HilbertCurve Hilbert Curve Properties The function jn is a root of n(j; The two claims to be proven are: 1) the sequence {fn} converges uniformly; The hilbert curve is a remarkable construct in many ways, but the thing that makes it useful in computer science is the fact that it has good clustering properties. If we take a curve like the one. This follows. Hilbert Curve Properties.
From octave.sourceforge.io
Function Reference hilbert_curve Hilbert Curve Properties 2) the limit function touches every point in the square. This follows from the existence of the dual isogeny. The hilbert curve is a remarkable construct in many ways, but the thing that makes it useful in computer science is the fact that it has good clustering properties. What is its equation or function? A nice description of hilbert curves. Hilbert Curve Properties.
From pythonturtle.academy
Hilbert Curve Learn Python Hilbert Curve Properties To prove 1), we note that in the interval [k4 − n, (k + 1)4 − n),. The two claims to be proven are: 2) the limit function touches every point in the square. The hilbert curve has always bugged me because it had no closed equation or function that i could find. A nice description of hilbert curves can. Hilbert Curve Properties.
From www.researchgate.net
The first six Hilbert curves, plotted from upper left to lower right Hilbert Curve Properties If we take a curve like the one. To prove 1), we note that in the interval [k4 − n, (k + 1)4 − n),. This follows from the existence of the dual isogeny. The hilbert curve has always bugged me because it had no closed equation or function that i could find. For example, if i wanted to find. Hilbert Curve Properties.
From jokergoo.github.io
HilbertCurve Hilbert Curve Properties 1) the sequence {fn} converges uniformly; The hilbert curve is a remarkable construct in many ways, but the thing that makes it useful in computer science is the fact that it has good clustering properties. To prove 1), we note that in the interval [k4 − n, (k + 1)4 − n),. The function jn is a root of n(j;. Hilbert Curve Properties.
From www.researchgate.net
Example of Hilbert curve generation (a) Order‐1, (b) Order‐2, (c) Order Hilbert Curve Properties To prove 1), we note that in the interval [k4 − n, (k + 1)4 − n),. The two claims to be proven are: A nice description of hilbert curves can be seen in grant sanderson’s (. The hilbert curve has always bugged me because it had no closed equation or function that i could find. What is its equation. Hilbert Curve Properties.
From manual.notch.one
Hilbert Curve Notch Manual 0.9.23 Hilbert Curve Properties To prove 1), we note that in the interval [k4 − n, (k + 1)4 − n),. For example, if i wanted to find the. A nice description of hilbert curves can be seen in grant sanderson’s (. The two claims to be proven are: 2) the limit function touches every point in the square. The function jn is a. Hilbert Curve Properties.
From www.bic.mni.mcgill.ca
Hilbert Space Filling Curves Hilbert Curve Properties To prove 1), we note that in the interval [k4 − n, (k + 1)4 − n),. For example, if i wanted to find the. The function jn is a root of n(j; The two claims to be proven are: The hilbert curve has always bugged me because it had no closed equation or function that i could find. The. Hilbert Curve Properties.
From www.researchgate.net
The modified 3D Hilbert curve of size 9 6 4 , constructed using the Hilbert Curve Properties 1) the sequence {fn} converges uniformly; The hilbert curve has always bugged me because it had no closed equation or function that i could find. A nice description of hilbert curves can be seen in grant sanderson’s (. The two claims to be proven are: For example, if i wanted to find the. To prove 1), we note that in. Hilbert Curve Properties.
From www.researchgate.net
Illustration of a 3D Hilbert space filling curve for 4 iterations Hilbert Curve Properties 1) the sequence {fn} converges uniformly; The hilbert curve is a remarkable construct in many ways, but the thing that makes it useful in computer science is the fact that it has good clustering properties. If we take a curve like the one. What is its equation or function? The function jn is a root of n(j; A nice description. Hilbert Curve Properties.
From www.researchgate.net
(a) Hilbert curve of order N=1. (b) Hilbert curve of order N=2. (c Hilbert Curve Properties The hilbert curve is a remarkable construct in many ways, but the thing that makes it useful in computer science is the fact that it has good clustering properties. The two claims to be proven are: 1) the sequence {fn} converges uniformly; If we take a curve like the one. To prove 1), we note that in the interval [k4. Hilbert Curve Properties.
From im.icerm.brown.edu
Perspectives on the Hilbert Curve Illustrating Mathematics Hilbert Curve Properties The two claims to be proven are: A nice description of hilbert curves can be seen in grant sanderson’s (. What is its equation or function? The function jn is a root of n(j; For example, if i wanted to find the. 2) the limit function touches every point in the square. If we take a curve like the one.. Hilbert Curve Properties.
From www.datagenetics.com
Hilbert Curves Hilbert Curve Properties This follows from the existence of the dual isogeny. 2) the limit function touches every point in the square. The hilbert curve is a remarkable construct in many ways, but the thing that makes it useful in computer science is the fact that it has good clustering properties. The two claims to be proven are: The hilbert curve has always. Hilbert Curve Properties.
From www.researchgate.net
The bijective mapping of the 3 th order iteration of the Hilbert curve Hilbert Curve Properties The function jn is a root of n(j; 2) the limit function touches every point in the square. If we take a curve like the one. A nice description of hilbert curves can be seen in grant sanderson’s (. The two claims to be proven are: The hilbert curve is a remarkable construct in many ways, but the thing that. Hilbert Curve Properties.
From quantum-journal.org
Hilbert curve vs Hilbert space exploiting fractal 2D covering to Hilbert Curve Properties 2) the limit function touches every point in the square. The two claims to be proven are: A nice description of hilbert curves can be seen in grant sanderson’s (. This follows from the existence of the dual isogeny. The function jn is a root of n(j; For example, if i wanted to find the. The hilbert curve has always. Hilbert Curve Properties.
From pixels.com
Hilbert Curves of Order 1 to 10 Digital Art by Martin Krzywinski Pixels Hilbert Curve Properties A nice description of hilbert curves can be seen in grant sanderson’s (. The hilbert curve has always bugged me because it had no closed equation or function that i could find. 2) the limit function touches every point in the square. The two claims to be proven are: What is its equation or function? This follows from the existence. Hilbert Curve Properties.
From www.youtube.com
Fractals Hilbert Curve A Practical Approach for Graphics Programming Hilbert Curve Properties 1) the sequence {fn} converges uniformly; A nice description of hilbert curves can be seen in grant sanderson’s (. What is its equation or function? The two claims to be proven are: This follows from the existence of the dual isogeny. 2) the limit function touches every point in the square. The function jn is a root of n(j; For. Hilbert Curve Properties.
From octave.sourceforge.io
Function Reference hilbert_curve Hilbert Curve Properties The two claims to be proven are: What is its equation or function? 1) the sequence {fn} converges uniformly; The hilbert curve is a remarkable construct in many ways, but the thing that makes it useful in computer science is the fact that it has good clustering properties. A nice description of hilbert curves can be seen in grant sanderson’s. Hilbert Curve Properties.
From www.semanticscholar.org
Table 1 from Arithmetic properties of homogeneous Hilbert curves Hilbert Curve Properties This follows from the existence of the dual isogeny. What is its equation or function? The two claims to be proven are: The hilbert curve has always bugged me because it had no closed equation or function that i could find. To prove 1), we note that in the interval [k4 − n, (k + 1)4 − n),. If we. Hilbert Curve Properties.
From www.researchgate.net
The side lengths of Hilbert curves with different orders (n = 1, 2, 3 Hilbert Curve Properties The two claims to be proven are: 2) the limit function touches every point in the square. 1) the sequence {fn} converges uniformly; The hilbert curve is a remarkable construct in many ways, but the thing that makes it useful in computer science is the fact that it has good clustering properties. What is its equation or function? This follows. Hilbert Curve Properties.
From www.brandongong.org
Three ways to draw Hilbert curves · Brandon Gong Hilbert Curve Properties 2) the limit function touches every point in the square. This follows from the existence of the dual isogeny. For example, if i wanted to find the. To prove 1), we note that in the interval [k4 − n, (k + 1)4 − n),. The hilbert curve is a remarkable construct in many ways, but the thing that makes it. Hilbert Curve Properties.
From www.researchgate.net
Recursive Hilbert curve generation. (a) Firstorder Hilbert curve of Hilbert Curve Properties A nice description of hilbert curves can be seen in grant sanderson’s (. What is its equation or function? To prove 1), we note that in the interval [k4 − n, (k + 1)4 − n),. This follows from the existence of the dual isogeny. The hilbert curve has always bugged me because it had no closed equation or function. Hilbert Curve Properties.
From awesomeopensource.com
Hilbert Curve Hilbert Curve Properties The hilbert curve is a remarkable construct in many ways, but the thing that makes it useful in computer science is the fact that it has good clustering properties. This follows from the existence of the dual isogeny. The hilbert curve has always bugged me because it had no closed equation or function that i could find. 1) the sequence. Hilbert Curve Properties.
From www.researchgate.net
Hilbert Structuredcube a) Hilbert curve iteration Hilbert Curve Properties The hilbert curve is a remarkable construct in many ways, but the thing that makes it useful in computer science is the fact that it has good clustering properties. 2) the limit function touches every point in the square. The two claims to be proven are: 1) the sequence {fn} converges uniformly; If we take a curve like the one.. Hilbert Curve Properties.
From www.researchgate.net
3. A 3dimensional, level 2 Hilbert curve. Download Scientific Diagram Hilbert Curve Properties A nice description of hilbert curves can be seen in grant sanderson’s (. 1) the sequence {fn} converges uniformly; What is its equation or function? 2) the limit function touches every point in the square. The function jn is a root of n(j; For example, if i wanted to find the. The hilbert curve is a remarkable construct in many. Hilbert Curve Properties.
From www.researchgate.net
First 6 steps toward building the Hilbert curve in two dimensions Hilbert Curve Properties What is its equation or function? The two claims to be proven are: 1) the sequence {fn} converges uniformly; For example, if i wanted to find the. The hilbert curve is a remarkable construct in many ways, but the thing that makes it useful in computer science is the fact that it has good clustering properties. A nice description of. Hilbert Curve Properties.
From www.reddit.com
Hilbert Curve, part 3 r/mathpics Hilbert Curve Properties A nice description of hilbert curves can be seen in grant sanderson’s (. The hilbert curve is a remarkable construct in many ways, but the thing that makes it useful in computer science is the fact that it has good clustering properties. For example, if i wanted to find the. The function jn is a root of n(j; The two. Hilbert Curve Properties.
From www.researchgate.net
Hilbert Curve and cropped image Download Scientific Diagram Hilbert Curve Properties The function jn is a root of n(j; 1) the sequence {fn} converges uniformly; The two claims to be proven are: 2) the limit function touches every point in the square. If we take a curve like the one. What is its equation or function? This follows from the existence of the dual isogeny. A nice description of hilbert curves. Hilbert Curve Properties.
From www.researchgate.net
The side lengths of Hilbert curves with different orders (n = 1, 2, 3 Hilbert Curve Properties A nice description of hilbert curves can be seen in grant sanderson’s (. The hilbert curve has always bugged me because it had no closed equation or function that i could find. To prove 1), we note that in the interval [k4 − n, (k + 1)4 − n),. What is its equation or function? For example, if i wanted. Hilbert Curve Properties.
From danbscott.ghost.io
Hilbert Curve Hilbert Curve Properties The two claims to be proven are: 2) the limit function touches every point in the square. To prove 1), we note that in the interval [k4 − n, (k + 1)4 − n),. What is its equation or function? For example, if i wanted to find the. This follows from the existence of the dual isogeny. If we take. Hilbert Curve Properties.
From www.researchgate.net
Hilbert curves in two dimensions for p = 1, 2, 3 Download Scientific Hilbert Curve Properties The function jn is a root of n(j; If we take a curve like the one. For example, if i wanted to find the. The hilbert curve has always bugged me because it had no closed equation or function that i could find. A nice description of hilbert curves can be seen in grant sanderson’s (. The hilbert curve is. Hilbert Curve Properties.
From www.researchgate.net
Different orders of Hilbert SpaceFilling Curves [30] Download Hilbert Curve Properties If we take a curve like the one. To prove 1), we note that in the interval [k4 − n, (k + 1)4 − n),. The hilbert curve has always bugged me because it had no closed equation or function that i could find. The two claims to be proven are: This follows from the existence of the dual isogeny.. Hilbert Curve Properties.
From www.researchgate.net
(PDF) characteristics of Hilbert curvebased metamaterials Hilbert Curve Properties For example, if i wanted to find the. What is its equation or function? 2) the limit function touches every point in the square. 1) the sequence {fn} converges uniformly; The hilbert curve has always bugged me because it had no closed equation or function that i could find. This follows from the existence of the dual isogeny. The function. Hilbert Curve Properties.
From www.researchgate.net
Hilbert curve and number. a Four basic subdivision modes of Hilbert Hilbert Curve Properties 2) the limit function touches every point in the square. This follows from the existence of the dual isogeny. If we take a curve like the one. The hilbert curve has always bugged me because it had no closed equation or function that i could find. The function jn is a root of n(j; What is its equation or function?. Hilbert Curve Properties.
From www.researchgate.net
A standard Hilbert curve of order 5. Download Scientific Diagram Hilbert Curve Properties The hilbert curve is a remarkable construct in many ways, but the thing that makes it useful in computer science is the fact that it has good clustering properties. This follows from the existence of the dual isogeny. If we take a curve like the one. 1) the sequence {fn} converges uniformly; The function jn is a root of n(j;. Hilbert Curve Properties.