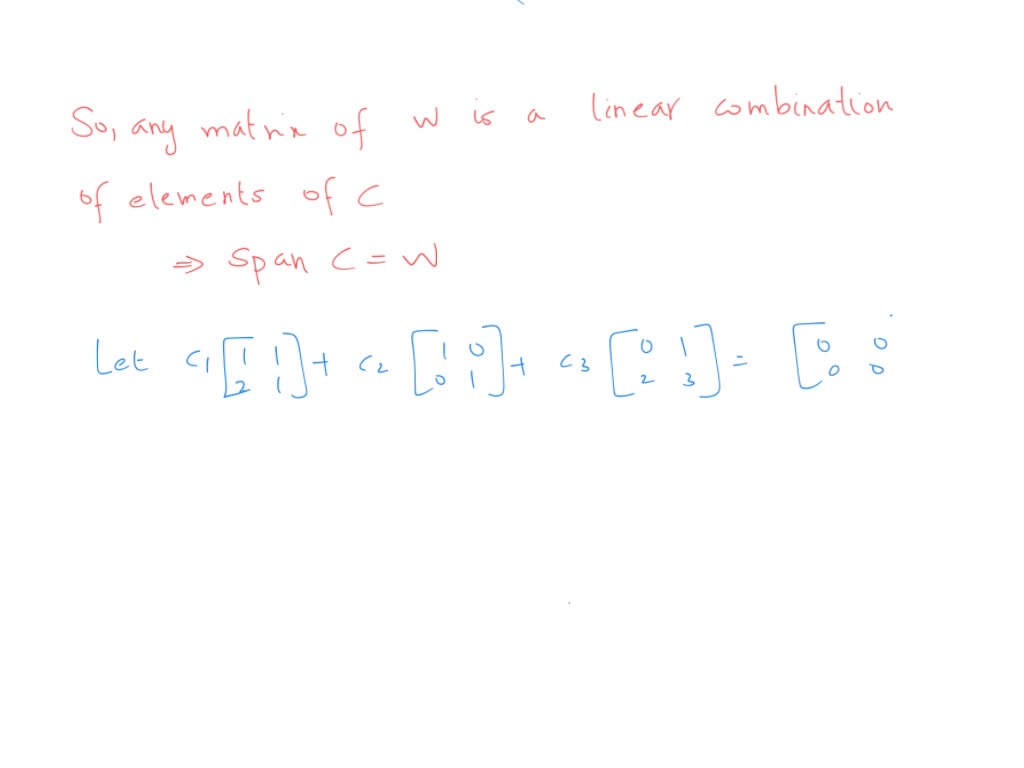Standard Basis Of The Space Of 2X2 Matrices . Here the vector space is 2x2. To find a basis for the space of 2×2 lower triangular matrices, we need to determine a set of linearly independent. In particular, \(\mathbb{r}^n \) has dimension \(n\). The set {b 1, b 2,., b r} is linearly independent. The standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. A basis for a vector space is by definition a spanning set which is linearly independent. S = span {b 1, b 2,., b r}. | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. In this simple presentation, i construct the standard basis in the space of 2x2. Let \(u\) be a vector space with basis \(b=\{u_1, \ldots, u_n\}\), and let \(u\) be a vector in \(u\). Because a basis “spans” the. A set of matrices that span the space and are linearly independent must be found in order to establish a basis for the space of. Form a basis for \(\mathbb{r}^n \). This is sometimes known as the standard basis. A set of vectors b = {b 1, b 2,., b r} is called a basis of a subspace s if.
from www.numerade.com
In particular, \(\mathbb{r}^n \) has dimension \(n\). Here the vector space is 2x2. Because a basis “spans” the. To find a basis for the space of 2×2 lower triangular matrices, we need to determine a set of linearly independent. This is sometimes known as the standard basis. | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. S = span {b 1, b 2,., b r}. The standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. In this simple presentation, i construct the standard basis in the space of 2x2. A basis for a vector space is by definition a spanning set which is linearly independent.
SOLVED Let W be the set of 2x2 matrices such that A ∈ W is a
Standard Basis Of The Space Of 2X2 Matrices Because a basis “spans” the. A set of vectors b = {b 1, b 2,., b r} is called a basis of a subspace s if. The standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. In particular, \(\mathbb{r}^n \) has dimension \(n\). To find a basis for the space of 2×2 lower triangular matrices, we need to determine a set of linearly independent. Let \(u\) be a vector space with basis \(b=\{u_1, \ldots, u_n\}\), and let \(u\) be a vector in \(u\). Form a basis for \(\mathbb{r}^n \). This is sometimes known as the standard basis. | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. S = span {b 1, b 2,., b r}. A basis for a vector space is by definition a spanning set which is linearly independent. A set of matrices that span the space and are linearly independent must be found in order to establish a basis for the space of. The set {b 1, b 2,., b r} is linearly independent. Because a basis “spans” the. In this simple presentation, i construct the standard basis in the space of 2x2. Here the vector space is 2x2.
From www.numerade.com
SOLVED Find a basis for the space of 2x2 diagonal matrices. basis Standard Basis Of The Space Of 2X2 Matrices Form a basis for \(\mathbb{r}^n \). Here the vector space is 2x2. Because a basis “spans” the. A set of matrices that span the space and are linearly independent must be found in order to establish a basis for the space of. Let \(u\) be a vector space with basis \(b=\{u_1, \ldots, u_n\}\), and let \(u\) be a vector in. Standard Basis Of The Space Of 2X2 Matrices.
From www.youtube.com
Use the Standard Basis to Find a Standard Matrix YouTube Standard Basis Of The Space Of 2X2 Matrices Form a basis for \(\mathbb{r}^n \). A set of vectors b = {b 1, b 2,., b r} is called a basis of a subspace s if. Because a basis “spans” the. | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. Let \(u\) be a vector space with basis \(b=\{u_1, \ldots, u_n\}\), and let. Standard Basis Of The Space Of 2X2 Matrices.
From www.youtube.com
P.4 Pauli matrices with Unit matrix form complete basis of complex Standard Basis Of The Space Of 2X2 Matrices S = span {b 1, b 2,., b r}. A set of matrices that span the space and are linearly independent must be found in order to establish a basis for the space of. Form a basis for \(\mathbb{r}^n \). This is sometimes known as the standard basis. A basis for a vector space is by definition a spanning set. Standard Basis Of The Space Of 2X2 Matrices.
From www.chegg.com
Solved The set B is a basis of the space of uppertriangular Standard Basis Of The Space Of 2X2 Matrices S = span {b 1, b 2,., b r}. This is sometimes known as the standard basis. To find a basis for the space of 2×2 lower triangular matrices, we need to determine a set of linearly independent. | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. Let \(u\) be a vector space with. Standard Basis Of The Space Of 2X2 Matrices.
From www.chegg.com
Solved MATH 3377 Activity 4 Vector Spaces The Vector Space Standard Basis Of The Space Of 2X2 Matrices Let \(u\) be a vector space with basis \(b=\{u_1, \ldots, u_n\}\), and let \(u\) be a vector in \(u\). A set of vectors b = {b 1, b 2,., b r} is called a basis of a subspace s if. S = span {b 1, b 2,., b r}. | | x | | = √x ⋅ x = √(x1)2. Standard Basis Of The Space Of 2X2 Matrices.
From www.youtube.com
Matrix addition 2x2 matrices in Pashto YouTube Standard Basis Of The Space Of 2X2 Matrices S = span {b 1, b 2,., b r}. A set of vectors b = {b 1, b 2,., b r} is called a basis of a subspace s if. In this simple presentation, i construct the standard basis in the space of 2x2. To find a basis for the space of 2×2 lower triangular matrices, we need to determine. Standard Basis Of The Space Of 2X2 Matrices.
From www.numerade.com
SOLVED R2x2 is the space of 2x2 matrices, so that R2x2 is the linear Standard Basis Of The Space Of 2X2 Matrices A set of vectors b = {b 1, b 2,., b r} is called a basis of a subspace s if. This is sometimes known as the standard basis. In this simple presentation, i construct the standard basis in the space of 2x2. The set {b 1, b 2,., b r} is linearly independent. A basis for a vector space. Standard Basis Of The Space Of 2X2 Matrices.
From www.storyofmathematics.com
Find a basis for the space of 2×2 lower triangular matrices. The Standard Basis Of The Space Of 2X2 Matrices The set {b 1, b 2,., b r} is linearly independent. | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. Let \(u\) be a vector space with basis \(b=\{u_1, \ldots, u_n\}\), and let \(u\) be a vector in \(u\). A set of matrices that span the space and are linearly independent must be found. Standard Basis Of The Space Of 2X2 Matrices.
From www.youtube.com
Finding a Standard Matrix Using the Standard Basis YouTube Standard Basis Of The Space Of 2X2 Matrices | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. This is sometimes known as the standard basis. Form a basis for \(\mathbb{r}^n \). A set of vectors b = {b 1, b 2,., b r} is called a basis of a subspace s if. In this simple presentation, i construct the standard basis in. Standard Basis Of The Space Of 2X2 Matrices.
From www.numerade.com
SOLVED Let Mi and Mz Consider the inner product = trace(AT B) in the Standard Basis Of The Space Of 2X2 Matrices | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. Form a basis for \(\mathbb{r}^n \). This is sometimes known as the standard basis. Because a basis “spans” the. A set of vectors b = {b 1, b 2,., b r} is called a basis of a subspace s if. S = span {b 1,. Standard Basis Of The Space Of 2X2 Matrices.
From www.chegg.com
Solved The vector space M2(R) of 2×2 real matrices has Standard Basis Of The Space Of 2X2 Matrices To find a basis for the space of 2×2 lower triangular matrices, we need to determine a set of linearly independent. A set of matrices that span the space and are linearly independent must be found in order to establish a basis for the space of. Here the vector space is 2x2. A set of vectors b = {b 1,. Standard Basis Of The Space Of 2X2 Matrices.
From www.chegg.com
Solved 64. Let V be the space of all upper triangular 2x 2 Standard Basis Of The Space Of 2X2 Matrices S = span {b 1, b 2,., b r}. The standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. This is sometimes known as the standard basis. A basis for a vector space is by definition a spanning set which is linearly independent. To find a basis for the space of 2×2 lower. Standard Basis Of The Space Of 2X2 Matrices.
From www.youtube.com
Finding a basis for a subset of 2x2 matrices YouTube Standard Basis Of The Space Of 2X2 Matrices Form a basis for \(\mathbb{r}^n \). The set {b 1, b 2,., b r} is linearly independent. Because a basis “spans” the. S = span {b 1, b 2,., b r}. | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. A set of matrices that span the space and are linearly independent must be. Standard Basis Of The Space Of 2X2 Matrices.
From www.numerade.com
SOLVED Let W be the set of 2x2 matrices such that A ∈ W is a Standard Basis Of The Space Of 2X2 Matrices A set of matrices that span the space and are linearly independent must be found in order to establish a basis for the space of. Form a basis for \(\mathbb{r}^n \). S = span {b 1, b 2,., b r}. | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. The standard notion of the. Standard Basis Of The Space Of 2X2 Matrices.
From www.youtube.com
dimension of subspace of 2x2 matrices MCQ MA Linear Algebra University Standard Basis Of The Space Of 2X2 Matrices Let \(u\) be a vector space with basis \(b=\{u_1, \ldots, u_n\}\), and let \(u\) be a vector in \(u\). Here the vector space is 2x2. To find a basis for the space of 2×2 lower triangular matrices, we need to determine a set of linearly independent. A set of matrices that span the space and are linearly independent must be. Standard Basis Of The Space Of 2X2 Matrices.
From www.animalia-life.club
Adding Matrices 2x2 Standard Basis Of The Space Of 2X2 Matrices Here the vector space is 2x2. Let \(u\) be a vector space with basis \(b=\{u_1, \ldots, u_n\}\), and let \(u\) be a vector in \(u\). In particular, \(\mathbb{r}^n \) has dimension \(n\). The set {b 1, b 2,., b r} is linearly independent. Form a basis for \(\mathbb{r}^n \). This is sometimes known as the standard basis. A set of. Standard Basis Of The Space Of 2X2 Matrices.
From www.youtube.com
Find a basis for the space of 2 \times 2 diagonal matrices.\text{Basis Standard Basis Of The Space Of 2X2 Matrices A set of matrices that span the space and are linearly independent must be found in order to establish a basis for the space of. | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. Form a basis for \(\mathbb{r}^n \). To find a basis for the space of 2×2 lower triangular matrices, we need. Standard Basis Of The Space Of 2X2 Matrices.
From www.numerade.com
point) Find a basis for the space of 2 x 2 lower triangular matrices Standard Basis Of The Space Of 2X2 Matrices Here the vector space is 2x2. A basis for a vector space is by definition a spanning set which is linearly independent. To find a basis for the space of 2×2 lower triangular matrices, we need to determine a set of linearly independent. Form a basis for \(\mathbb{r}^n \). Because a basis “spans” the. S = span {b 1, b. Standard Basis Of The Space Of 2X2 Matrices.
From www.slideserve.com
PPT Consider the 2x2 matrix PowerPoint Presentation, free download Standard Basis Of The Space Of 2X2 Matrices Form a basis for \(\mathbb{r}^n \). A basis for a vector space is by definition a spanning set which is linearly independent. The standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. A set of vectors b = {b 1, b 2,., b r} is called a basis of a subspace s if.. Standard Basis Of The Space Of 2X2 Matrices.
From www.numerade.com
SOLVED point) Consider the ordered bases B = [; [ and c={[+ [5 Standard Basis Of The Space Of 2X2 Matrices This is sometimes known as the standard basis. In particular, \(\mathbb{r}^n \) has dimension \(n\). A set of matrices that span the space and are linearly independent must be found in order to establish a basis for the space of. The set {b 1, b 2,., b r} is linearly independent. Let \(u\) be a vector space with basis \(b=\{u_1,. Standard Basis Of The Space Of 2X2 Matrices.
From www.numerade.com
SOLVED Recall that M2,2 is the vector space of 2x2 matrices Define the Standard Basis Of The Space Of 2X2 Matrices This is sometimes known as the standard basis. In particular, \(\mathbb{r}^n \) has dimension \(n\). Form a basis for \(\mathbb{r}^n \). To find a basis for the space of 2×2 lower triangular matrices, we need to determine a set of linearly independent. The set {b 1, b 2,., b r} is linearly independent. | | x | | = √x. Standard Basis Of The Space Of 2X2 Matrices.
From www.youtube.com
Tutorial Q79 Pauli matrices basis in 2x2 matrices, Part I YouTube Standard Basis Of The Space Of 2X2 Matrices A set of vectors b = {b 1, b 2,., b r} is called a basis of a subspace s if. | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. A basis for a vector space is by definition a spanning set which is linearly independent. The set {b 1, b 2,., b r}. Standard Basis Of The Space Of 2X2 Matrices.
From www.slideserve.com
PPT 2x2 Matrices, Determinants and Inverses PowerPoint Presentation Standard Basis Of The Space Of 2X2 Matrices To find a basis for the space of 2×2 lower triangular matrices, we need to determine a set of linearly independent. S = span {b 1, b 2,., b r}. The standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. This is sometimes known as the standard basis. A set of matrices that. Standard Basis Of The Space Of 2X2 Matrices.
From www.researchgate.net
A 2x2 matrix is defined by its columns, image of the basis vectors Standard Basis Of The Space Of 2X2 Matrices | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. Because a basis “spans” the. This is sometimes known as the standard basis. S = span {b 1, b 2,., b r}. In this simple presentation, i construct the standard basis in the space of 2x2. A set of matrices that span the space and. Standard Basis Of The Space Of 2X2 Matrices.
From www.chegg.com
Solved b) Consider the vector space of symmetric 2 x 2 Standard Basis Of The Space Of 2X2 Matrices A set of vectors b = {b 1, b 2,., b r} is called a basis of a subspace s if. Here the vector space is 2x2. Form a basis for \(\mathbb{r}^n \). To find a basis for the space of 2×2 lower triangular matrices, we need to determine a set of linearly independent. The standard notion of the length. Standard Basis Of The Space Of 2X2 Matrices.
From www.youtube.com
Find the eigenvalues and eigenvectors of a 2x2 matrix YouTube Standard Basis Of The Space Of 2X2 Matrices Form a basis for \(\mathbb{r}^n \). Because a basis “spans” the. Let \(u\) be a vector space with basis \(b=\{u_1, \ldots, u_n\}\), and let \(u\) be a vector in \(u\). A set of matrices that span the space and are linearly independent must be found in order to establish a basis for the space of. Here the vector space is. Standard Basis Of The Space Of 2X2 Matrices.
From www.numerade.com
SOLVED (1 point) The set [ ][ ][ ] is called the standard basis Standard Basis Of The Space Of 2X2 Matrices Form a basis for \(\mathbb{r}^n \). A basis for a vector space is by definition a spanning set which is linearly independent. In this simple presentation, i construct the standard basis in the space of 2x2. The standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. Here the vector space is 2x2. |. Standard Basis Of The Space Of 2X2 Matrices.
From www.youtube.com
Matrix with respect to a basis YouTube Standard Basis Of The Space Of 2X2 Matrices Because a basis “spans” the. A set of vectors b = {b 1, b 2,., b r} is called a basis of a subspace s if. The set {b 1, b 2,., b r} is linearly independent. To find a basis for the space of 2×2 lower triangular matrices, we need to determine a set of linearly independent. The standard. Standard Basis Of The Space Of 2X2 Matrices.
From www.youtube.com
Tutorial Q78 Basis in vector space of 2x2 matrices YouTube Standard Basis Of The Space Of 2X2 Matrices In particular, \(\mathbb{r}^n \) has dimension \(n\). Here the vector space is 2x2. Form a basis for \(\mathbb{r}^n \). A basis for a vector space is by definition a spanning set which is linearly independent. A set of vectors b = {b 1, b 2,., b r} is called a basis of a subspace s if. | | x |. Standard Basis Of The Space Of 2X2 Matrices.
From www.chegg.com
Solved Let V Be The Vector Space Of All 2x2 Upper Triangu... Standard Basis Of The Space Of 2X2 Matrices Form a basis for \(\mathbb{r}^n \). A basis for a vector space is by definition a spanning set which is linearly independent. Let \(u\) be a vector space with basis \(b=\{u_1, \ldots, u_n\}\), and let \(u\) be a vector in \(u\). A set of matrices that span the space and are linearly independent must be found in order to establish. Standard Basis Of The Space Of 2X2 Matrices.
From www.chegg.com
Solved Let V = R^(2x2) be the vector space of all 2 x 2 Standard Basis Of The Space Of 2X2 Matrices This is sometimes known as the standard basis. Because a basis “spans” the. S = span {b 1, b 2,., b r}. Form a basis for \(\mathbb{r}^n \). | | x | | = √x ⋅ x = √(x1)2 + (x2)2 + ⋯(xn)2. Here the vector space is 2x2. The standard notion of the length of a vector x =. Standard Basis Of The Space Of 2X2 Matrices.
From www.cs.princeton.edu
2x2 Matrices Standard Basis Of The Space Of 2X2 Matrices In particular, \(\mathbb{r}^n \) has dimension \(n\). The standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. The set {b 1, b 2,., b r} is linearly independent. This is sometimes known as the standard basis. Let \(u\) be a vector space with basis \(b=\{u_1, \ldots, u_n\}\), and let \(u\) be a vector. Standard Basis Of The Space Of 2X2 Matrices.
From www.numerade.com
SOLVED (1 point) Let 6 and Mz = M] =[1 Consider the inner product (4 Standard Basis Of The Space Of 2X2 Matrices A set of matrices that span the space and are linearly independent must be found in order to establish a basis for the space of. A basis for a vector space is by definition a spanning set which is linearly independent. In this simple presentation, i construct the standard basis in the space of 2x2. Form a basis for \(\mathbb{r}^n. Standard Basis Of The Space Of 2X2 Matrices.
From www.chegg.com
Solved Let M2.2 be the vector space of all 2 x 2 matrices Standard Basis Of The Space Of 2X2 Matrices Form a basis for \(\mathbb{r}^n \). Let \(u\) be a vector space with basis \(b=\{u_1, \ldots, u_n\}\), and let \(u\) be a vector in \(u\). The set {b 1, b 2,., b r} is linearly independent. The standard notion of the length of a vector x = (x1, x2,., xn) ∈ rn is. This is sometimes known as the standard. Standard Basis Of The Space Of 2X2 Matrices.
From www.youtube.com
Linear Transformations Projection of X and Y Axis Using 2x2 Matrix Standard Basis Of The Space Of 2X2 Matrices This is sometimes known as the standard basis. To find a basis for the space of 2×2 lower triangular matrices, we need to determine a set of linearly independent. Because a basis “spans” the. The set {b 1, b 2,., b r} is linearly independent. A set of vectors b = {b 1, b 2,., b r} is called a. Standard Basis Of The Space Of 2X2 Matrices.