Orthogonal Matrix With Inner Product . But , therefore , (uv) is an orthogonal matrix. This does, using the above. This is because of the polarization identities. Inner product (or ‘dot product’) divided by the products of their lengths. An orthogonal matrix, u, is a square invertible matrix such that : Learn more about the orthogonal. Here, rm nis the space of real m. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. Also, the product of an orthogonal matrix and its transpose is equal to i. For an inner product space, an isometry also preserves the inner product: The standard inner product between matrices is hx;yi= tr(xty) = x i x j x ijy ij where x;y 2rm n. However in general you can define an orthogonal matrix as commuting with the inner product. Thus if our linear transformation preserves lengths of vectors.
from ssaru.github.io
This is because of the polarization identities. Inner product (or ‘dot product’) divided by the products of their lengths. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. An orthogonal matrix, u, is a square invertible matrix such that : But , therefore , (uv) is an orthogonal matrix. For an inner product space, an isometry also preserves the inner product: Here, rm nis the space of real m. Thus if our linear transformation preserves lengths of vectors. This does, using the above. Learn more about the orthogonal.
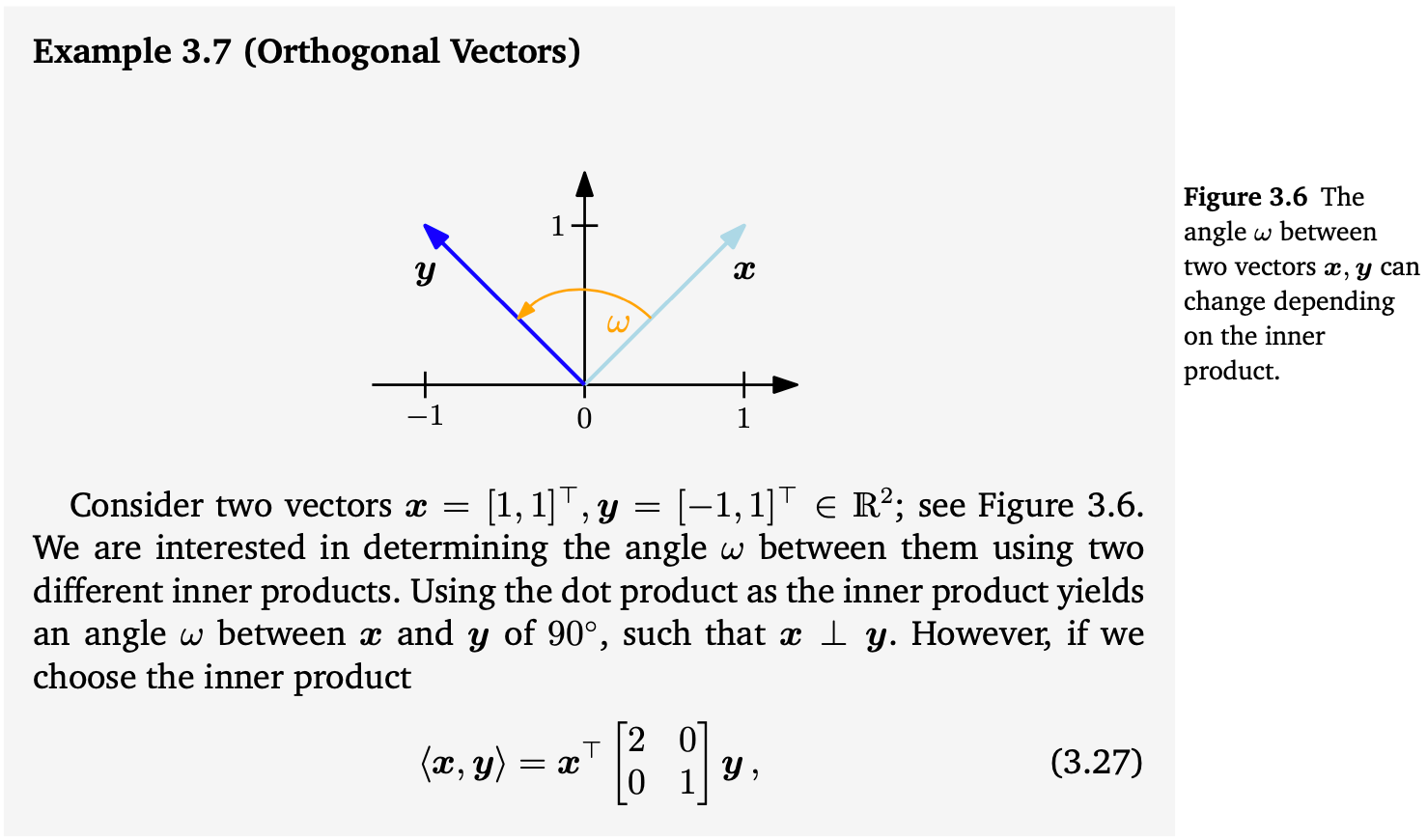
(MML Book 선형대수 Chapter 3.4) Angles and Orthogonality Martin Hwang
Orthogonal Matrix With Inner Product However in general you can define an orthogonal matrix as commuting with the inner product. Here, rm nis the space of real m. Learn more about the orthogonal. An orthogonal matrix, u, is a square invertible matrix such that : Thus if our linear transformation preserves lengths of vectors. Also, the product of an orthogonal matrix and its transpose is equal to i. Inner product (or ‘dot product’) divided by the products of their lengths. But , therefore , (uv) is an orthogonal matrix. The standard inner product between matrices is hx;yi= tr(xty) = x i x j x ijy ij where x;y 2rm n. However in general you can define an orthogonal matrix as commuting with the inner product. This is because of the polarization identities. This does, using the above. For an inner product space, an isometry also preserves the inner product: A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose.
From www.youtube.com
Orthogonal Matrix What is orthogonal Matrix Important Questions on Orthogonal Matrix With Inner Product This is because of the polarization identities. The standard inner product between matrices is hx;yi= tr(xty) = x i x j x ijy ij where x;y 2rm n. But , therefore , (uv) is an orthogonal matrix. An orthogonal matrix, u, is a square invertible matrix such that : Inner product (or ‘dot product’) divided by the products of their. Orthogonal Matrix With Inner Product.
From math.stackexchange.com
inner product space GramSchmidt algorithm used for obtaining the Orthogonal Matrix With Inner Product This is because of the polarization identities. The standard inner product between matrices is hx;yi= tr(xty) = x i x j x ijy ij where x;y 2rm n. This does, using the above. For an inner product space, an isometry also preserves the inner product: Inner product (or ‘dot product’) divided by the products of their lengths. But , therefore. Orthogonal Matrix With Inner Product.
From www.learndatasci.com
Orthogonal and Orthonormal Vectors LearnDataSci Orthogonal Matrix With Inner Product Inner product (or ‘dot product’) divided by the products of their lengths. Also, the product of an orthogonal matrix and its transpose is equal to i. For an inner product space, an isometry also preserves the inner product: This is because of the polarization identities. Thus if our linear transformation preserves lengths of vectors. The standard inner product between matrices. Orthogonal Matrix With Inner Product.
From www.numerade.com
SOLVED Show that the product of two orthogonal matrices is also an Orthogonal Matrix With Inner Product However in general you can define an orthogonal matrix as commuting with the inner product. For an inner product space, an isometry also preserves the inner product: Here, rm nis the space of real m. The standard inner product between matrices is hx;yi= tr(xty) = x i x j x ijy ij where x;y 2rm n. Also, the product of. Orthogonal Matrix With Inner Product.
From math.stackexchange.com
linear algebra What is wrong with my proof that x^Hy = x^Ty for any Orthogonal Matrix With Inner Product Also, the product of an orthogonal matrix and its transpose is equal to i. Inner product (or ‘dot product’) divided by the products of their lengths. However in general you can define an orthogonal matrix as commuting with the inner product. An orthogonal matrix, u, is a square invertible matrix such that : Thus if our linear transformation preserves lengths. Orthogonal Matrix With Inner Product.
From www.youtube.com
【Orthogonality】06 Orthogonal matrix YouTube Orthogonal Matrix With Inner Product Learn more about the orthogonal. An orthogonal matrix, u, is a square invertible matrix such that : The standard inner product between matrices is hx;yi= tr(xty) = x i x j x ijy ij where x;y 2rm n. This is because of the polarization identities. But , therefore , (uv) is an orthogonal matrix. However in general you can define. Orthogonal Matrix With Inner Product.
From slideplayer.com
Introduction The central problems of Linear Algebra are to study the Orthogonal Matrix With Inner Product For an inner product space, an isometry also preserves the inner product: This does, using the above. Here, rm nis the space of real m. An orthogonal matrix, u, is a square invertible matrix such that : However in general you can define an orthogonal matrix as commuting with the inner product. But , therefore , (uv) is an orthogonal. Orthogonal Matrix With Inner Product.
From math.stackexchange.com
linear algebra change of basis and inner product in non orthogonal Orthogonal Matrix With Inner Product Also, the product of an orthogonal matrix and its transpose is equal to i. For an inner product space, an isometry also preserves the inner product: A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. The standard inner product between matrices is hx;yi= tr(xty) = x i x j x ijy ij where. Orthogonal Matrix With Inner Product.
From limfadreams.weebly.com
Orthogonal matrix limfadreams Orthogonal Matrix With Inner Product But , therefore , (uv) is an orthogonal matrix. For an inner product space, an isometry also preserves the inner product: The standard inner product between matrices is hx;yi= tr(xty) = x i x j x ijy ij where x;y 2rm n. An orthogonal matrix, u, is a square invertible matrix such that : Thus if our linear transformation preserves. Orthogonal Matrix With Inner Product.
From dxoaxhuxq.blob.core.windows.net
Orthogonal Matrix Inner Product at Edie Doran blog Orthogonal Matrix With Inner Product An orthogonal matrix, u, is a square invertible matrix such that : But , therefore , (uv) is an orthogonal matrix. This does, using the above. Also, the product of an orthogonal matrix and its transpose is equal to i. This is because of the polarization identities. However in general you can define an orthogonal matrix as commuting with the. Orthogonal Matrix With Inner Product.
From ssaru.github.io
(MML Book 선형대수 Chapter 3.4) Angles and Orthogonality Martin Hwang Orthogonal Matrix With Inner Product Thus if our linear transformation preserves lengths of vectors. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. But , therefore , (uv) is an orthogonal matrix. The standard inner product between matrices is hx;yi= tr(xty) = x i x j x ijy ij where x;y 2rm n. Here, rm nis the space. Orthogonal Matrix With Inner Product.
From mathematica.stackexchange.com
Output the tensor product of two matrix as a matrix Mathematica Stack Orthogonal Matrix With Inner Product This does, using the above. But , therefore , (uv) is an orthogonal matrix. For an inner product space, an isometry also preserves the inner product: This is because of the polarization identities. Learn more about the orthogonal. However in general you can define an orthogonal matrix as commuting with the inner product. Inner product (or ‘dot product’) divided by. Orthogonal Matrix With Inner Product.
From www.youtube.com
Inner product vs dot product YouTube Orthogonal Matrix With Inner Product Learn more about the orthogonal. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. Also, the product of an orthogonal matrix and its transpose is equal to i. Thus if our linear transformation preserves lengths of vectors. This does, using the above. The standard inner product between matrices is hx;yi= tr(xty) = x. Orthogonal Matrix With Inner Product.
From www.slideserve.com
PPT Elementary Linear Algebra Anton & Rorres, 9 th Edition PowerPoint Orthogonal Matrix With Inner Product A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. However in general you can define an orthogonal matrix as commuting with the inner product. An orthogonal matrix, u, is a square invertible matrix such that : For an inner product space, an isometry also preserves the inner product: This does, using the above.. Orthogonal Matrix With Inner Product.
From www.youtube.com
What is Orthogonal Matrix and its Properties Kamaldheeriya YouTube Orthogonal Matrix With Inner Product Also, the product of an orthogonal matrix and its transpose is equal to i. But , therefore , (uv) is an orthogonal matrix. Here, rm nis the space of real m. An orthogonal matrix, u, is a square invertible matrix such that : This does, using the above. Learn more about the orthogonal. For an inner product space, an isometry. Orthogonal Matrix With Inner Product.
From dxovlehoe.blob.core.windows.net
Example Orthogonal Matrix at Verena Cowan blog Orthogonal Matrix With Inner Product But , therefore , (uv) is an orthogonal matrix. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. An orthogonal matrix, u, is a square invertible matrix such that : This does, using the above. Inner product (or ‘dot product’) divided by the products of their lengths. For an inner product space, an. Orthogonal Matrix With Inner Product.
From www.slideserve.com
PPT Elementary Linear Algebra Anton & Rorres, 9 th Edition PowerPoint Orthogonal Matrix With Inner Product A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. However in general you can define an orthogonal matrix as commuting with the inner product. But , therefore , (uv) is an orthogonal matrix. An orthogonal matrix, u, is a square invertible matrix such that : The standard inner product between matrices is hx;yi=. Orthogonal Matrix With Inner Product.
From www.youtube.com
Linear Algebra Inner Product, Vector Length, Orthogonality YouTube Orthogonal Matrix With Inner Product For an inner product space, an isometry also preserves the inner product: A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. Also, the product of an orthogonal matrix and its transpose is equal to i. An orthogonal matrix, u, is a square invertible matrix such that : This does, using the above. Inner. Orthogonal Matrix With Inner Product.
From solvedlib.com
View vectors in R" as nx matrices. For u and in … SolvedLib Orthogonal Matrix With Inner Product This is because of the polarization identities. This does, using the above. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. But , therefore , (uv) is an orthogonal matrix. For an inner product space, an isometry also preserves the inner product: Learn more about the orthogonal. The standard inner product between matrices. Orthogonal Matrix With Inner Product.
From demonstrations.wolfram.com
Orthogonality of Two Functions with Weighted Inner Products Wolfram Orthogonal Matrix With Inner Product Thus if our linear transformation preserves lengths of vectors. Here, rm nis the space of real m. An orthogonal matrix, u, is a square invertible matrix such that : A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. For an inner product space, an isometry also preserves the inner product: The standard inner. Orthogonal Matrix With Inner Product.
From www.coursehero.com
[Solved] Finding the orthogonal basis using the GramSchmidt process Orthogonal Matrix With Inner Product This does, using the above. An orthogonal matrix, u, is a square invertible matrix such that : Inner product (or ‘dot product’) divided by the products of their lengths. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. However in general you can define an orthogonal matrix as commuting with the inner product.. Orthogonal Matrix With Inner Product.
From www.coursehero.com
[Solved] Let T be the orthogonal projection onto a subspace V of R n Orthogonal Matrix With Inner Product However in general you can define an orthogonal matrix as commuting with the inner product. Here, rm nis the space of real m. The standard inner product between matrices is hx;yi= tr(xty) = x i x j x ijy ij where x;y 2rm n. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose.. Orthogonal Matrix With Inner Product.
From www.chegg.com
Solved Let VR2x2 be the vector space of all 2 × 2 matrices Orthogonal Matrix With Inner Product This does, using the above. The standard inner product between matrices is hx;yi= tr(xty) = x i x j x ijy ij where x;y 2rm n. An orthogonal matrix, u, is a square invertible matrix such that : But , therefore , (uv) is an orthogonal matrix. This is because of the polarization identities. Inner product (or ‘dot product’) divided. Orthogonal Matrix With Inner Product.
From www.chegg.com
Solved Consider R3 with the standard inner product given by Orthogonal Matrix With Inner Product Here, rm nis the space of real m. Thus if our linear transformation preserves lengths of vectors. But , therefore , (uv) is an orthogonal matrix. An orthogonal matrix, u, is a square invertible matrix such that : The standard inner product between matrices is hx;yi= tr(xty) = x i x j x ijy ij where x;y 2rm n. However. Orthogonal Matrix With Inner Product.
From www.youtube.com
Outer product vs inner product, and matrix representation of operator Orthogonal Matrix With Inner Product Inner product (or ‘dot product’) divided by the products of their lengths. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. The standard inner product between matrices is hx;yi= tr(xty) = x i x j x ijy ij where x;y 2rm n. Also, the product of an orthogonal matrix and its transpose is. Orthogonal Matrix With Inner Product.
From www.chegg.com
Solved a. Which of the matrices are orthogonal (has Orthogonal Matrix With Inner Product This is because of the polarization identities. For an inner product space, an isometry also preserves the inner product: Inner product (or ‘dot product’) divided by the products of their lengths. This does, using the above. Learn more about the orthogonal. But , therefore , (uv) is an orthogonal matrix. The standard inner product between matrices is hx;yi= tr(xty) =. Orthogonal Matrix With Inner Product.
From www.youtube.com
Properties of Orthogonal Matrix Example1 YouTube Orthogonal Matrix With Inner Product But , therefore , (uv) is an orthogonal matrix. Here, rm nis the space of real m. Thus if our linear transformation preserves lengths of vectors. For an inner product space, an isometry also preserves the inner product: The standard inner product between matrices is hx;yi= tr(xty) = x i x j x ijy ij where x;y 2rm n. However. Orthogonal Matrix With Inner Product.
From math.stackexchange.com
linear algebra How can an inner product be defined through a proof Orthogonal Matrix With Inner Product An orthogonal matrix, u, is a square invertible matrix such that : But , therefore , (uv) is an orthogonal matrix. Learn more about the orthogonal. Also, the product of an orthogonal matrix and its transpose is equal to i. Here, rm nis the space of real m. Thus if our linear transformation preserves lengths of vectors. The standard inner. Orthogonal Matrix With Inner Product.
From datascienceparichay.com
Numpy Check If a Matrix is Orthogonal Data Science Parichay Orthogonal Matrix With Inner Product The standard inner product between matrices is hx;yi= tr(xty) = x i x j x ijy ij where x;y 2rm n. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. Inner product (or ‘dot product’) divided by the products of their lengths. But , therefore , (uv) is an orthogonal matrix. This does,. Orthogonal Matrix With Inner Product.
From math.stackexchange.com
linear algebra For any inner product, can we always find a symmetric Orthogonal Matrix With Inner Product An orthogonal matrix, u, is a square invertible matrix such that : However in general you can define an orthogonal matrix as commuting with the inner product. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. Here, rm nis the space of real m. Learn more about the orthogonal. This is because of. Orthogonal Matrix With Inner Product.
From www.slideserve.com
PPT ENGG2013 Unit 19 The principal axes theorem PowerPoint Orthogonal Matrix With Inner Product This is because of the polarization identities. Learn more about the orthogonal. An orthogonal matrix, u, is a square invertible matrix such that : Here, rm nis the space of real m. For an inner product space, an isometry also preserves the inner product: A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose.. Orthogonal Matrix With Inner Product.
From www.slideserve.com
PPT Chapter 7 Inner Product Spaces PowerPoint Presentation, free Orthogonal Matrix With Inner Product This is because of the polarization identities. An orthogonal matrix, u, is a square invertible matrix such that : Here, rm nis the space of real m. Learn more about the orthogonal. Inner product (or ‘dot product’) divided by the products of their lengths. However in general you can define an orthogonal matrix as commuting with the inner product. This. Orthogonal Matrix With Inner Product.
From www.youtube.com
How to Prove that a Matrix is Orthogonal YouTube Orthogonal Matrix With Inner Product This is because of the polarization identities. Inner product (or ‘dot product’) divided by the products of their lengths. Thus if our linear transformation preserves lengths of vectors. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. For an inner product space, an isometry also preserves the inner product: Here, rm nis the. Orthogonal Matrix With Inner Product.
From math.stackexchange.com
linear algebra Why does the fact that "Tv is orthogonal to v for Orthogonal Matrix With Inner Product An orthogonal matrix, u, is a square invertible matrix such that : For an inner product space, an isometry also preserves the inner product: But , therefore , (uv) is an orthogonal matrix. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. Thus if our linear transformation preserves lengths of vectors. Learn more. Orthogonal Matrix With Inner Product.
From www.youtube.com
Orthogonal Matrix Definition Example Properties Class 12 Maths YouTube Orthogonal Matrix With Inner Product Inner product (or ‘dot product’) divided by the products of their lengths. Here, rm nis the space of real m. The standard inner product between matrices is hx;yi= tr(xty) = x i x j x ijy ij where x;y 2rm n. This is because of the polarization identities. However in general you can define an orthogonal matrix as commuting with. Orthogonal Matrix With Inner Product.