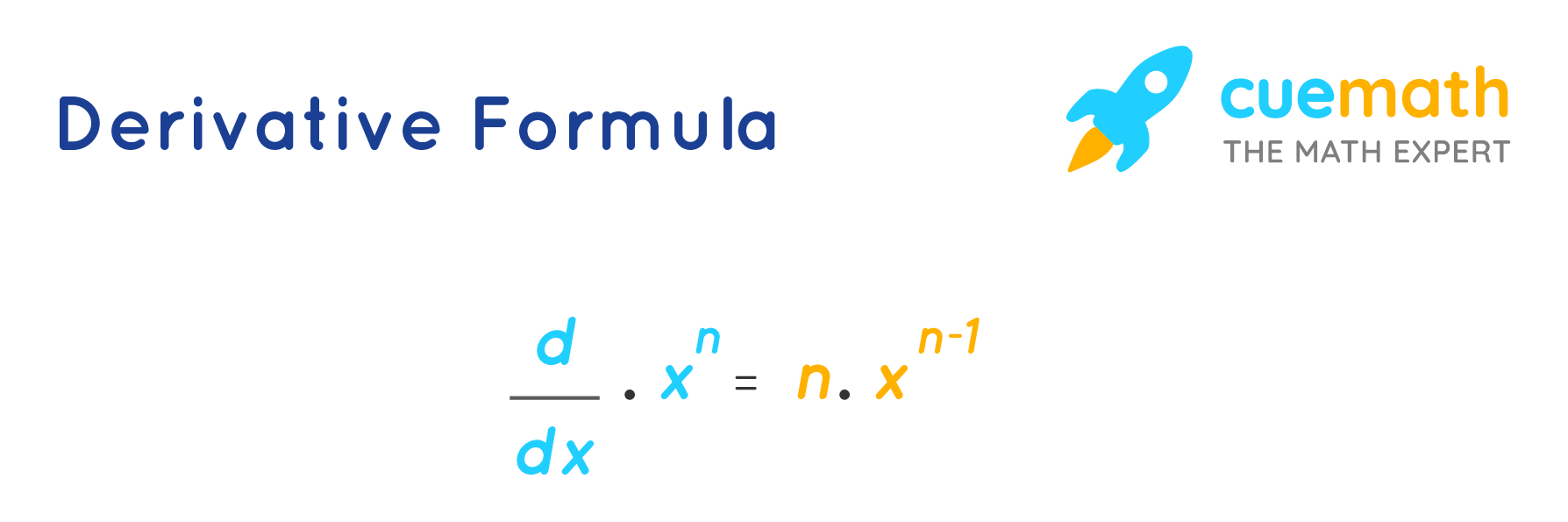Derivatives Math Examples . Change divided by time is one example of a rate. Scroll down the page for more examples and solutions. Here is a set of practice problems to accompany the differentiation formulas section of the derivatives chapter of the notes. In this section we look at some applications of the derivative by focusing on the interpretation of the derivative as the rate of change of a function. Here are useful rules to help you work out the derivatives of many functions (with examples below). For example, if we want to know the derivative at x = 1, we would plug 1 into the derivative to find that: The functions describing the examples above involve a change over time. The following formulas give the definition of derivative. To find the derivative at a given point, we simply plug in the x value. F' (x) = f' (1) = 2 (1) =. The little mark ’ means derivative. The rates of change in the previous.
from www.cuemath.com
The following formulas give the definition of derivative. Here are useful rules to help you work out the derivatives of many functions (with examples below). The functions describing the examples above involve a change over time. The rates of change in the previous. Here is a set of practice problems to accompany the differentiation formulas section of the derivatives chapter of the notes. For example, if we want to know the derivative at x = 1, we would plug 1 into the derivative to find that: The little mark ’ means derivative. Change divided by time is one example of a rate. To find the derivative at a given point, we simply plug in the x value. F' (x) = f' (1) = 2 (1) =.
Derivative Formula Learn Formula to Find Derivatives
Derivatives Math Examples To find the derivative at a given point, we simply plug in the x value. The little mark ’ means derivative. To find the derivative at a given point, we simply plug in the x value. Change divided by time is one example of a rate. In this section we look at some applications of the derivative by focusing on the interpretation of the derivative as the rate of change of a function. Scroll down the page for more examples and solutions. The functions describing the examples above involve a change over time. F' (x) = f' (1) = 2 (1) =. The rates of change in the previous. For example, if we want to know the derivative at x = 1, we would plug 1 into the derivative to find that: Here are useful rules to help you work out the derivatives of many functions (with examples below). Here is a set of practice problems to accompany the differentiation formulas section of the derivatives chapter of the notes. The following formulas give the definition of derivative.
From isacork2017.com
Basic Derivatives Practice Worksheet Isacork Derivatives Math Examples Change divided by time is one example of a rate. The rates of change in the previous. Here is a set of practice problems to accompany the differentiation formulas section of the derivatives chapter of the notes. For example, if we want to know the derivative at x = 1, we would plug 1 into the derivative to find that:. Derivatives Math Examples.
From www.cuemath.com
Derivative Formula What is Derivative Formula? Examples Derivatives Math Examples Here are useful rules to help you work out the derivatives of many functions (with examples below). F' (x) = f' (1) = 2 (1) =. The rates of change in the previous. The little mark ’ means derivative. In this section we look at some applications of the derivative by focusing on the interpretation of the derivative as the. Derivatives Math Examples.
From www.geeksforgeeks.org
Derivative Formulas List Differentiation Formulas with Examples Derivatives Math Examples Change divided by time is one example of a rate. F' (x) = f' (1) = 2 (1) =. The little mark ’ means derivative. Here is a set of practice problems to accompany the differentiation formulas section of the derivatives chapter of the notes. Here are useful rules to help you work out the derivatives of many functions (with. Derivatives Math Examples.
From www.studypool.com
SOLUTION Calculus Derivative Multiple Choice Questions Studypool Derivatives Math Examples Here are useful rules to help you work out the derivatives of many functions (with examples below). The following formulas give the definition of derivative. Scroll down the page for more examples and solutions. The rates of change in the previous. For example, if we want to know the derivative at x = 1, we would plug 1 into the. Derivatives Math Examples.
From www.cuemath.com
Derivatives Calculus, Meaning, Interpretation Derivatives Math Examples The functions describing the examples above involve a change over time. In this section we look at some applications of the derivative by focusing on the interpretation of the derivative as the rate of change of a function. The little mark ’ means derivative. Scroll down the page for more examples and solutions. To find the derivative at a given. Derivatives Math Examples.
From www.youtube.com
Calculus 1 Derivatives YouTube Derivatives Math Examples The little mark ’ means derivative. The following formulas give the definition of derivative. For example, if we want to know the derivative at x = 1, we would plug 1 into the derivative to find that: Here is a set of practice problems to accompany the differentiation formulas section of the derivatives chapter of the notes. The functions describing. Derivatives Math Examples.
From ar.inspiredpencil.com
Differentiation Calculus Examples Derivatives Math Examples The rates of change in the previous. Here is a set of practice problems to accompany the differentiation formulas section of the derivatives chapter of the notes. The following formulas give the definition of derivative. Here are useful rules to help you work out the derivatives of many functions (with examples below). In this section we look at some applications. Derivatives Math Examples.
From www.youtube.com
Definition of the Derivative YouTube Derivatives Math Examples Scroll down the page for more examples and solutions. F' (x) = f' (1) = 2 (1) =. For example, if we want to know the derivative at x = 1, we would plug 1 into the derivative to find that: The functions describing the examples above involve a change over time. Here is a set of practice problems to. Derivatives Math Examples.
From www.eeweb.com
Calculus Derivatives, Rules, and Limits Cheat Sheet EE Derivatives Math Examples The little mark ’ means derivative. Scroll down the page for more examples and solutions. To find the derivative at a given point, we simply plug in the x value. F' (x) = f' (1) = 2 (1) =. Change divided by time is one example of a rate. For example, if we want to know the derivative at x. Derivatives Math Examples.
From www.math-exercises.com
Math Exercises & Math Problems Derivative of a Function Derivatives Math Examples For example, if we want to know the derivative at x = 1, we would plug 1 into the derivative to find that: In this section we look at some applications of the derivative by focusing on the interpretation of the derivative as the rate of change of a function. To find the derivative at a given point, we simply. Derivatives Math Examples.
From www.onlinemathlearning.com
Calculus Derivative Rules (video lessons, examples, solutions) Derivatives Math Examples For example, if we want to know the derivative at x = 1, we would plug 1 into the derivative to find that: The little mark ’ means derivative. F' (x) = f' (1) = 2 (1) =. Here are useful rules to help you work out the derivatives of many functions (with examples below). Scroll down the page for. Derivatives Math Examples.
From www.youtube.com
Calculus Introduction to Derivatives YouTube Derivatives Math Examples Scroll down the page for more examples and solutions. F' (x) = f' (1) = 2 (1) =. The rates of change in the previous. For example, if we want to know the derivative at x = 1, we would plug 1 into the derivative to find that: The functions describing the examples above involve a change over time. Change. Derivatives Math Examples.
From www.youtube.com
Calculus The basic rules for derivatives YouTube Derivatives Math Examples The following formulas give the definition of derivative. Here is a set of practice problems to accompany the differentiation formulas section of the derivatives chapter of the notes. Here are useful rules to help you work out the derivatives of many functions (with examples below). Change divided by time is one example of a rate. The functions describing the examples. Derivatives Math Examples.
From www.teachoo.com
Differentiation Formulas & Rules Basic,Trig Full list Teachoo Derivatives Math Examples Change divided by time is one example of a rate. Here is a set of practice problems to accompany the differentiation formulas section of the derivatives chapter of the notes. The rates of change in the previous. Scroll down the page for more examples and solutions. The functions describing the examples above involve a change over time. For example, if. Derivatives Math Examples.
From calcworkshop.com
Derivative Of Inverse Functions (How To w/ Examples!) Derivatives Math Examples In this section we look at some applications of the derivative by focusing on the interpretation of the derivative as the rate of change of a function. The rates of change in the previous. Scroll down the page for more examples and solutions. F' (x) = f' (1) = 2 (1) =. Change divided by time is one example of. Derivatives Math Examples.
From www.tes.com
Calculus Differentiation Teaching Resources Derivatives Math Examples To find the derivative at a given point, we simply plug in the x value. F' (x) = f' (1) = 2 (1) =. Here is a set of practice problems to accompany the differentiation formulas section of the derivatives chapter of the notes. The following formulas give the definition of derivative. Here are useful rules to help you work. Derivatives Math Examples.
From andymath.com
Definition of Derivative Derivatives Math Examples For example, if we want to know the derivative at x = 1, we would plug 1 into the derivative to find that: Change divided by time is one example of a rate. The functions describing the examples above involve a change over time. F' (x) = f' (1) = 2 (1) =. To find the derivative at a given. Derivatives Math Examples.
From mathoriginal.com
Derivative Rules Power, Product and Sum rules Math Original Derivatives Math Examples The little mark ’ means derivative. Change divided by time is one example of a rate. Scroll down the page for more examples and solutions. The rates of change in the previous. Here are useful rules to help you work out the derivatives of many functions (with examples below). F' (x) = f' (1) = 2 (1) =. Here is. Derivatives Math Examples.
From owlcation.com
What Is Calculus? A Beginner's Guide to Limits and Differentiation Derivatives Math Examples To find the derivative at a given point, we simply plug in the x value. The functions describing the examples above involve a change over time. Change divided by time is one example of a rate. The rates of change in the previous. F' (x) = f' (1) = 2 (1) =. Here are useful rules to help you work. Derivatives Math Examples.
From www.chegg.com
Solved Solve The Following Basic Calculus Problems A. D/... Derivatives Math Examples Change divided by time is one example of a rate. Scroll down the page for more examples and solutions. To find the derivative at a given point, we simply plug in the x value. The rates of change in the previous. Here is a set of practice problems to accompany the differentiation formulas section of the derivatives chapter of the. Derivatives Math Examples.
From pleacher.com
List of Derivative Formulas Derivatives Math Examples F' (x) = f' (1) = 2 (1) =. In this section we look at some applications of the derivative by focusing on the interpretation of the derivative as the rate of change of a function. Here is a set of practice problems to accompany the differentiation formulas section of the derivatives chapter of the notes. For example, if we. Derivatives Math Examples.
From math.stackexchange.com
calculus Derivative of piecewise functions Mathematics Stack Exchange Derivatives Math Examples Scroll down the page for more examples and solutions. The functions describing the examples above involve a change over time. The rates of change in the previous. Here is a set of practice problems to accompany the differentiation formulas section of the derivatives chapter of the notes. For example, if we want to know the derivative at x = 1,. Derivatives Math Examples.
From www.math-exercises.com
Math Exercises & Math Problems Derivative of a Function Derivatives Math Examples The following formulas give the definition of derivative. Here is a set of practice problems to accompany the differentiation formulas section of the derivatives chapter of the notes. The rates of change in the previous. The little mark ’ means derivative. The functions describing the examples above involve a change over time. To find the derivative at a given point,. Derivatives Math Examples.
From calcworkshop.com
Higher Order Derivatives Derivatives Math Examples The following formulas give the definition of derivative. To find the derivative at a given point, we simply plug in the x value. The little mark ’ means derivative. Scroll down the page for more examples and solutions. For example, if we want to know the derivative at x = 1, we would plug 1 into the derivative to find. Derivatives Math Examples.
From www.youtube.com
Calculus Differentiation Examples Derivative of Algebraic functions Derivatives Math Examples Change divided by time is one example of a rate. The little mark ’ means derivative. To find the derivative at a given point, we simply plug in the x value. The following formulas give the definition of derivative. Scroll down the page for more examples and solutions. For example, if we want to know the derivative at x =. Derivatives Math Examples.
From calcworkshop.com
Limit Definition Of Derivative (Defined w/ Examples!) Derivatives Math Examples The functions describing the examples above involve a change over time. For example, if we want to know the derivative at x = 1, we would plug 1 into the derivative to find that: Here are useful rules to help you work out the derivatives of many functions (with examples below). To find the derivative at a given point, we. Derivatives Math Examples.
From www.theacetutors.com
Derivative Rules Cheat Sheet Calculus Ace Tutors Blog Derivatives Math Examples The rates of change in the previous. Here are useful rules to help you work out the derivatives of many functions (with examples below). For example, if we want to know the derivative at x = 1, we would plug 1 into the derivative to find that: F' (x) = f' (1) = 2 (1) =. The little mark ’. Derivatives Math Examples.
From www.cuemath.com
Derivative Formula Learn Formula to Find Derivatives Derivatives Math Examples In this section we look at some applications of the derivative by focusing on the interpretation of the derivative as the rate of change of a function. F' (x) = f' (1) = 2 (1) =. The little mark ’ means derivative. Change divided by time is one example of a rate. Here is a set of practice problems to. Derivatives Math Examples.
From mattwins.blogspot.com
[Mattwins] Calculus Rules of Derivatives Derivatives Math Examples The functions describing the examples above involve a change over time. In this section we look at some applications of the derivative by focusing on the interpretation of the derivative as the rate of change of a function. For example, if we want to know the derivative at x = 1, we would plug 1 into the derivative to find. Derivatives Math Examples.
From www.youtube.com
Calculus The Derivative YouTube Derivatives Math Examples The little mark ’ means derivative. Scroll down the page for more examples and solutions. Here are useful rules to help you work out the derivatives of many functions (with examples below). For example, if we want to know the derivative at x = 1, we would plug 1 into the derivative to find that: The rates of change in. Derivatives Math Examples.
From evgenii.com
Basic derivatives Derivatives Math Examples The functions describing the examples above involve a change over time. Scroll down the page for more examples and solutions. Here is a set of practice problems to accompany the differentiation formulas section of the derivatives chapter of the notes. Change divided by time is one example of a rate. Here are useful rules to help you work out the. Derivatives Math Examples.
From www.showme.com
Definition of the DerivativeExamples Math, Calculus ShowMe Derivatives Math Examples Here are useful rules to help you work out the derivatives of many functions (with examples below). For example, if we want to know the derivative at x = 1, we would plug 1 into the derivative to find that: Scroll down the page for more examples and solutions. The functions describing the examples above involve a change over time.. Derivatives Math Examples.
From www.hyper-ad.com
Math Help Calculus Properties of Derivatives Technical Tutoring Derivatives Math Examples In this section we look at some applications of the derivative by focusing on the interpretation of the derivative as the rate of change of a function. The functions describing the examples above involve a change over time. Change divided by time is one example of a rate. To find the derivative at a given point, we simply plug in. Derivatives Math Examples.
From www.youtube.com
Calculus Basic Derivative Rules YouTube Derivatives Math Examples For example, if we want to know the derivative at x = 1, we would plug 1 into the derivative to find that: The functions describing the examples above involve a change over time. F' (x) = f' (1) = 2 (1) =. In this section we look at some applications of the derivative by focusing on the interpretation of. Derivatives Math Examples.
From www.cuemath.com
Derivatives Calculus, Meaning, Interpretation Derivatives Math Examples F' (x) = f' (1) = 2 (1) =. The little mark ’ means derivative. The following formulas give the definition of derivative. Scroll down the page for more examples and solutions. To find the derivative at a given point, we simply plug in the x value. In this section we look at some applications of the derivative by focusing. Derivatives Math Examples.