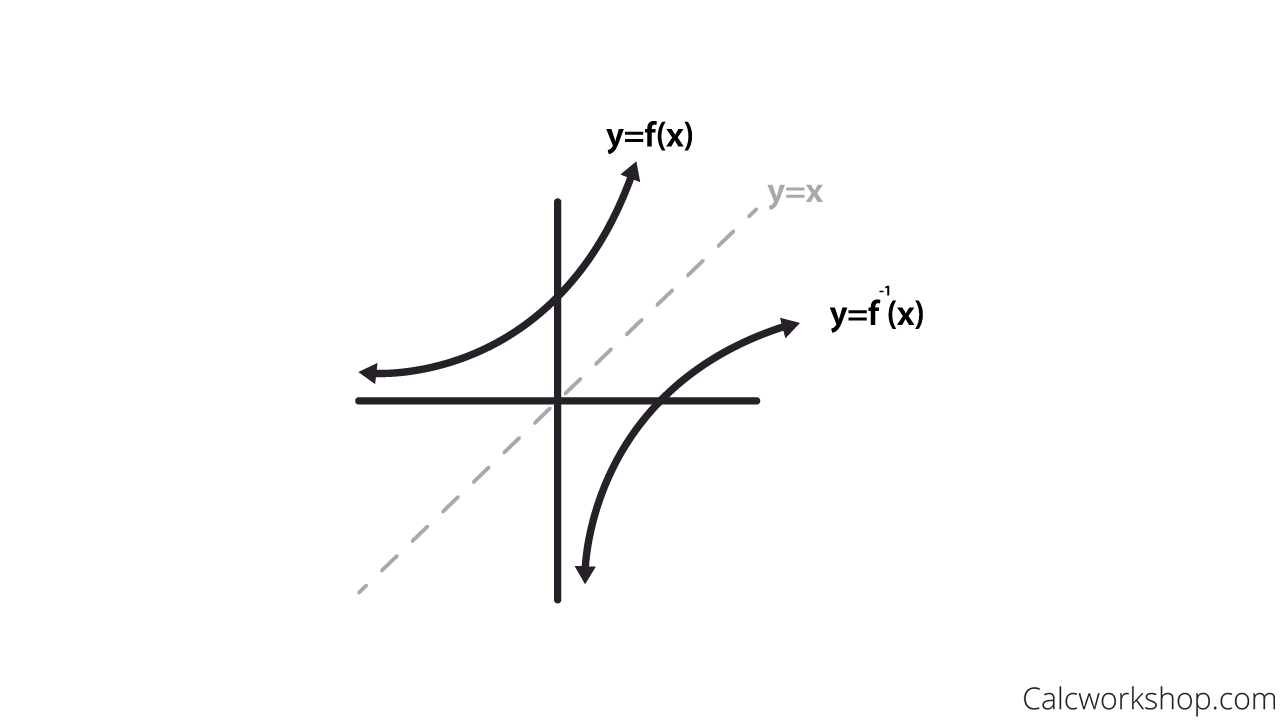
What Is The Purpose Of The Inverse Function . An inverse function of a function f simply undoes the action performed by the function f. Learn the definition, graph, examples, practice problems, and more. An inverse function reverses the operation done by a particular function. In other words, whatever a function does, the inverse function undoes it. The inverse of the function to get the original amount back, or simply calculate the other currency, one must use the inverse. In this section, we define an inverse. The inverse of a function \ (f\) is another function \ (f_ {inv}\) defined so that \ (f (f_ {inv} (x)) = x\) and \ (f_ {inv} (f (x)) = x\) both hold. So a bijective function follows stricter rules than a general function, which allows us to have an inverse. A function has to be bijective to have an inverse.
from calcworkshop.com
Learn the definition, graph, examples, practice problems, and more. So a bijective function follows stricter rules than a general function, which allows us to have an inverse. The inverse of a function \ (f\) is another function \ (f_ {inv}\) defined so that \ (f (f_ {inv} (x)) = x\) and \ (f_ {inv} (f (x)) = x\) both hold. In other words, whatever a function does, the inverse function undoes it. In this section, we define an inverse. An inverse function of a function f simply undoes the action performed by the function f. A function has to be bijective to have an inverse. The inverse of the function to get the original amount back, or simply calculate the other currency, one must use the inverse. An inverse function reverses the operation done by a particular function.
How to Graph and Find Inverse Functions (19 Terrific Examples!)
What Is The Purpose Of The Inverse Function The inverse of a function \ (f\) is another function \ (f_ {inv}\) defined so that \ (f (f_ {inv} (x)) = x\) and \ (f_ {inv} (f (x)) = x\) both hold. The inverse of the function to get the original amount back, or simply calculate the other currency, one must use the inverse. An inverse function reverses the operation done by a particular function. An inverse function of a function f simply undoes the action performed by the function f. A function has to be bijective to have an inverse. In other words, whatever a function does, the inverse function undoes it. So a bijective function follows stricter rules than a general function, which allows us to have an inverse. The inverse of a function \ (f\) is another function \ (f_ {inv}\) defined so that \ (f (f_ {inv} (x)) = x\) and \ (f_ {inv} (f (x)) = x\) both hold. In this section, we define an inverse. Learn the definition, graph, examples, practice problems, and more.
From www.slideserve.com
PPT 6.3 Inverse Functions PowerPoint Presentation, free download ID692333 What Is The Purpose Of The Inverse Function Learn the definition, graph, examples, practice problems, and more. The inverse of a function \ (f\) is another function \ (f_ {inv}\) defined so that \ (f (f_ {inv} (x)) = x\) and \ (f_ {inv} (f (x)) = x\) both hold. An inverse function of a function f simply undoes the action performed by the function f. In other. What Is The Purpose Of The Inverse Function.
From www.cuemath.com
Inverse Function Formula Learn the Formula to Find the Inverse of a Function What Is The Purpose Of The Inverse Function A function has to be bijective to have an inverse. In other words, whatever a function does, the inverse function undoes it. Learn the definition, graph, examples, practice problems, and more. The inverse of a function \ (f\) is another function \ (f_ {inv}\) defined so that \ (f (f_ {inv} (x)) = x\) and \ (f_ {inv} (f (x)). What Is The Purpose Of The Inverse Function.
From www.chegg.com
Solved What is the domain of the inverse function of What Is The Purpose Of The Inverse Function An inverse function reverses the operation done by a particular function. An inverse function of a function f simply undoes the action performed by the function f. Learn the definition, graph, examples, practice problems, and more. A function has to be bijective to have an inverse. The inverse of a function \ (f\) is another function \ (f_ {inv}\) defined. What Is The Purpose Of The Inverse Function.
From www.youtube.com
Verifying Inverse Functions Precalculus YouTube What Is The Purpose Of The Inverse Function A function has to be bijective to have an inverse. An inverse function of a function f simply undoes the action performed by the function f. The inverse of the function to get the original amount back, or simply calculate the other currency, one must use the inverse. In this section, we define an inverse. The inverse of a function. What Is The Purpose Of The Inverse Function.
From www.youtube.com
Math 1A/1B. PreCalculus Inverse Functions YouTube What Is The Purpose Of The Inverse Function An inverse function reverses the operation done by a particular function. The inverse of the function to get the original amount back, or simply calculate the other currency, one must use the inverse. In other words, whatever a function does, the inverse function undoes it. So a bijective function follows stricter rules than a general function, which allows us to. What Is The Purpose Of The Inverse Function.
From www.youtube.com
Introduction to Inverse Functions YouTube What Is The Purpose Of The Inverse Function Learn the definition, graph, examples, practice problems, and more. In other words, whatever a function does, the inverse function undoes it. In this section, we define an inverse. The inverse of the function to get the original amount back, or simply calculate the other currency, one must use the inverse. A function has to be bijective to have an inverse.. What Is The Purpose Of The Inverse Function.
From www.youtube.com
Graphing Inverse Functions YouTube What Is The Purpose Of The Inverse Function A function has to be bijective to have an inverse. Learn the definition, graph, examples, practice problems, and more. An inverse function of a function f simply undoes the action performed by the function f. The inverse of a function \ (f\) is another function \ (f_ {inv}\) defined so that \ (f (f_ {inv} (x)) = x\) and \. What Is The Purpose Of The Inverse Function.
From www.slideshare.net
Inverse functions What Is The Purpose Of The Inverse Function A function has to be bijective to have an inverse. So a bijective function follows stricter rules than a general function, which allows us to have an inverse. An inverse function reverses the operation done by a particular function. In other words, whatever a function does, the inverse function undoes it. The inverse of a function \ (f\) is another. What Is The Purpose Of The Inverse Function.
From www.slideserve.com
PPT 6.3 Inverse Functions PowerPoint Presentation ID692333 What Is The Purpose Of The Inverse Function In other words, whatever a function does, the inverse function undoes it. The inverse of a function \ (f\) is another function \ (f_ {inv}\) defined so that \ (f (f_ {inv} (x)) = x\) and \ (f_ {inv} (f (x)) = x\) both hold. A function has to be bijective to have an inverse. In this section, we define. What Is The Purpose Of The Inverse Function.
From spmaddmaths.blog.onlinetuition.com.my
Inverse Function Example 1 SPM Additional Mathematics What Is The Purpose Of The Inverse Function So a bijective function follows stricter rules than a general function, which allows us to have an inverse. An inverse function of a function f simply undoes the action performed by the function f. Learn the definition, graph, examples, practice problems, and more. The inverse of a function \ (f\) is another function \ (f_ {inv}\) defined so that \. What Is The Purpose Of The Inverse Function.
From www.onlinemathlearning.com
Inverse Functions (examples, solutions, videos, activities) What Is The Purpose Of The Inverse Function In this section, we define an inverse. In other words, whatever a function does, the inverse function undoes it. A function has to be bijective to have an inverse. An inverse function of a function f simply undoes the action performed by the function f. The inverse of a function \ (f\) is another function \ (f_ {inv}\) defined so. What Is The Purpose Of The Inverse Function.
From www.pinterest.com
Evaluating Inverse Trigonometric Functions, Basic Introduction, Examples... Trigonometric What Is The Purpose Of The Inverse Function The inverse of a function \ (f\) is another function \ (f_ {inv}\) defined so that \ (f (f_ {inv} (x)) = x\) and \ (f_ {inv} (f (x)) = x\) both hold. An inverse function of a function f simply undoes the action performed by the function f. So a bijective function follows stricter rules than a general function,. What Is The Purpose Of The Inverse Function.
From www.slideshare.net
Inverse functions and relations What Is The Purpose Of The Inverse Function In other words, whatever a function does, the inverse function undoes it. So a bijective function follows stricter rules than a general function, which allows us to have an inverse. In this section, we define an inverse. An inverse function reverses the operation done by a particular function. The inverse of the function to get the original amount back, or. What Is The Purpose Of The Inverse Function.
From eevibes.com
How to determine the inverse of a function give an example? EEVibes What Is The Purpose Of The Inverse Function So a bijective function follows stricter rules than a general function, which allows us to have an inverse. An inverse function of a function f simply undoes the action performed by the function f. In other words, whatever a function does, the inverse function undoes it. Learn the definition, graph, examples, practice problems, and more. An inverse function reverses the. What Is The Purpose Of The Inverse Function.
From ar.inspiredpencil.com
Examples Of Function And Its Inverse What Is The Purpose Of The Inverse Function In this section, we define an inverse. Learn the definition, graph, examples, practice problems, and more. So a bijective function follows stricter rules than a general function, which allows us to have an inverse. An inverse function of a function f simply undoes the action performed by the function f. In other words, whatever a function does, the inverse function. What Is The Purpose Of The Inverse Function.
From calcworkshop.com
How to Graph and Find Inverse Functions (19 Terrific Examples!) What Is The Purpose Of The Inverse Function So a bijective function follows stricter rules than a general function, which allows us to have an inverse. The inverse of a function \ (f\) is another function \ (f_ {inv}\) defined so that \ (f (f_ {inv} (x)) = x\) and \ (f_ {inv} (f (x)) = x\) both hold. Learn the definition, graph, examples, practice problems, and more.. What Is The Purpose Of The Inverse Function.
From www.storyofmathematics.com
Inverse of a Function Explanation & Examples What Is The Purpose Of The Inverse Function A function has to be bijective to have an inverse. The inverse of the function to get the original amount back, or simply calculate the other currency, one must use the inverse. In this section, we define an inverse. In other words, whatever a function does, the inverse function undoes it. An inverse function reverses the operation done by a. What Is The Purpose Of The Inverse Function.
From www.youtube.com
20. Find the Inverse Function of f(x) = 2x 7 YouTube What Is The Purpose Of The Inverse Function So a bijective function follows stricter rules than a general function, which allows us to have an inverse. The inverse of the function to get the original amount back, or simply calculate the other currency, one must use the inverse. An inverse function reverses the operation done by a particular function. In other words, whatever a function does, the inverse. What Is The Purpose Of The Inverse Function.
From telgurus.co.uk
What is an Inverse function? Definition, Examples, method What Is The Purpose Of The Inverse Function The inverse of a function \ (f\) is another function \ (f_ {inv}\) defined so that \ (f (f_ {inv} (x)) = x\) and \ (f_ {inv} (f (x)) = x\) both hold. A function has to be bijective to have an inverse. So a bijective function follows stricter rules than a general function, which allows us to have an. What Is The Purpose Of The Inverse Function.
From www.youtube.com
How To Find The Inverse of a Function YouTube What Is The Purpose Of The Inverse Function An inverse function reverses the operation done by a particular function. A function has to be bijective to have an inverse. The inverse of a function \ (f\) is another function \ (f_ {inv}\) defined so that \ (f (f_ {inv} (x)) = x\) and \ (f_ {inv} (f (x)) = x\) both hold. In this section, we define an. What Is The Purpose Of The Inverse Function.
From www.youtube.com
How to find the inverse of a function example YouTube What Is The Purpose Of The Inverse Function An inverse function of a function f simply undoes the action performed by the function f. The inverse of a function \ (f\) is another function \ (f_ {inv}\) defined so that \ (f (f_ {inv} (x)) = x\) and \ (f_ {inv} (f (x)) = x\) both hold. In this section, we define an inverse. The inverse of the. What Is The Purpose Of The Inverse Function.
From www.wikihow.com
How to Algebraically Find the Inverse of a Function 5 Steps What Is The Purpose Of The Inverse Function The inverse of the function to get the original amount back, or simply calculate the other currency, one must use the inverse. An inverse function reverses the operation done by a particular function. A function has to be bijective to have an inverse. Learn the definition, graph, examples, practice problems, and more. The inverse of a function \ (f\) is. What Is The Purpose Of The Inverse Function.
From www.mathskey.com
Given the graph of the inverse function below, What Is The Purpose Of The Inverse Function In other words, whatever a function does, the inverse function undoes it. Learn the definition, graph, examples, practice problems, and more. So a bijective function follows stricter rules than a general function, which allows us to have an inverse. An inverse function reverses the operation done by a particular function. The inverse of the function to get the original amount. What Is The Purpose Of The Inverse Function.
From www.slideserve.com
PPT Inverse Functions Objectives PowerPoint Presentation, free download ID6298865 What Is The Purpose Of The Inverse Function So a bijective function follows stricter rules than a general function, which allows us to have an inverse. In other words, whatever a function does, the inverse function undoes it. The inverse of the function to get the original amount back, or simply calculate the other currency, one must use the inverse. In this section, we define an inverse. Learn. What Is The Purpose Of The Inverse Function.
From mathsathome.com
How to Find an Inverse Function What Is The Purpose Of The Inverse Function In this section, we define an inverse. In other words, whatever a function does, the inverse function undoes it. An inverse function of a function f simply undoes the action performed by the function f. The inverse of the function to get the original amount back, or simply calculate the other currency, one must use the inverse. An inverse function. What Is The Purpose Of The Inverse Function.
From www.mashupmath.com
Finding the Inverse of a Function Complete Guide — Mashup Math What Is The Purpose Of The Inverse Function Learn the definition, graph, examples, practice problems, and more. In this section, we define an inverse. So a bijective function follows stricter rules than a general function, which allows us to have an inverse. The inverse of the function to get the original amount back, or simply calculate the other currency, one must use the inverse. The inverse of a. What Is The Purpose Of The Inverse Function.
From thirdspacelearning.com
Inverse Functions GCSE Maths Steps, Examples & Worksheet What Is The Purpose Of The Inverse Function A function has to be bijective to have an inverse. An inverse function of a function f simply undoes the action performed by the function f. An inverse function reverses the operation done by a particular function. Learn the definition, graph, examples, practice problems, and more. So a bijective function follows stricter rules than a general function, which allows us. What Is The Purpose Of The Inverse Function.
From www.wikihow.com
How to Find the Inverse of a Function 4 Steps (with Pictures) What Is The Purpose Of The Inverse Function An inverse function reverses the operation done by a particular function. In other words, whatever a function does, the inverse function undoes it. An inverse function of a function f simply undoes the action performed by the function f. A function has to be bijective to have an inverse. So a bijective function follows stricter rules than a general function,. What Is The Purpose Of The Inverse Function.
From www.inertialearning.com
Inverse Functions InertiaLearning What Is The Purpose Of The Inverse Function Learn the definition, graph, examples, practice problems, and more. In other words, whatever a function does, the inverse function undoes it. In this section, we define an inverse. The inverse of the function to get the original amount back, or simply calculate the other currency, one must use the inverse. So a bijective function follows stricter rules than a general. What Is The Purpose Of The Inverse Function.
From www.youtube.com
How to Find and Graph the Inverse of a Function Algebra 2 Math Video YouTube What Is The Purpose Of The Inverse Function A function has to be bijective to have an inverse. The inverse of the function to get the original amount back, or simply calculate the other currency, one must use the inverse. An inverse function reverses the operation done by a particular function. Learn the definition, graph, examples, practice problems, and more. So a bijective function follows stricter rules than. What Is The Purpose Of The Inverse Function.
From www.youtube.com
Derivative of Inverse Functions Calculus 1 YouTube What Is The Purpose Of The Inverse Function Learn the definition, graph, examples, practice problems, and more. An inverse function of a function f simply undoes the action performed by the function f. The inverse of a function \ (f\) is another function \ (f_ {inv}\) defined so that \ (f (f_ {inv} (x)) = x\) and \ (f_ {inv} (f (x)) = x\) both hold. A function. What Is The Purpose Of The Inverse Function.
From owlcation.com
How to Find the Inverse of a Function (With Examples) Owlcation What Is The Purpose Of The Inverse Function In this section, we define an inverse. The inverse of a function \ (f\) is another function \ (f_ {inv}\) defined so that \ (f (f_ {inv} (x)) = x\) and \ (f_ {inv} (f (x)) = x\) both hold. So a bijective function follows stricter rules than a general function, which allows us to have an inverse. In other. What Is The Purpose Of The Inverse Function.
From spmaddmaths.blog.onlinetuition.com.my
Inverse Function SPM Additional Mathematics What Is The Purpose Of The Inverse Function An inverse function of a function f simply undoes the action performed by the function f. In other words, whatever a function does, the inverse function undoes it. So a bijective function follows stricter rules than a general function, which allows us to have an inverse. The inverse of the function to get the original amount back, or simply calculate. What Is The Purpose Of The Inverse Function.
From www.ck12.org
OneStep Equations and Inverse Operations CK12 Foundation What Is The Purpose Of The Inverse Function The inverse of the function to get the original amount back, or simply calculate the other currency, one must use the inverse. Learn the definition, graph, examples, practice problems, and more. In this section, we define an inverse. The inverse of a function \ (f\) is another function \ (f_ {inv}\) defined so that \ (f (f_ {inv} (x)) =. What Is The Purpose Of The Inverse Function.
From worksheetlistmo.z21.web.core.windows.net
How To Graph Inverse Functions What Is The Purpose Of The Inverse Function The inverse of the function to get the original amount back, or simply calculate the other currency, one must use the inverse. So a bijective function follows stricter rules than a general function, which allows us to have an inverse. A function has to be bijective to have an inverse. In this section, we define an inverse. Learn the definition,. What Is The Purpose Of The Inverse Function.