N Vs Log N Complexity . Specifically, it indicates that the time. This order of time complexity can be seen in cases where an n * n matrix needs to be sorted along the rows. $$ dividing through by $\log(n^n)$ yields $$. So yes in terms of complexity $\mathcal{o}(\log{}n)$ is faster. With that we have $\log^2n =\log n * \log n \geq \log n$ (since $\log n \geq 1$). A quick select on finding kth element in an. The notation o (log n) represents logarithmic time complexity in algorithm analysis. When you have a single loop within. We understand the logarithmic aspect of time complexity and we understand n*log(n)’s relation to linear time complexity,. I am wondering if this time complexity difference between n log n and n are significant in real life. It is a mistake when taken in the context that o(n) and o(n log n) functions have better complexity than o(1) and o(log n). When the input size is reduced by half, maybe when iterating, handling recursion, or whatsoever, it is a logarithmic time complexity (o(log n)).
from web.stanford.edu
We understand the logarithmic aspect of time complexity and we understand n*log(n)’s relation to linear time complexity,. When the input size is reduced by half, maybe when iterating, handling recursion, or whatsoever, it is a logarithmic time complexity (o(log n)). So yes in terms of complexity $\mathcal{o}(\log{}n)$ is faster. The notation o (log n) represents logarithmic time complexity in algorithm analysis. This order of time complexity can be seen in cases where an n * n matrix needs to be sorted along the rows. It is a mistake when taken in the context that o(n) and o(n log n) functions have better complexity than o(1) and o(log n). A quick select on finding kth element in an. Specifically, it indicates that the time. With that we have $\log^2n =\log n * \log n \geq \log n$ (since $\log n \geq 1$). When you have a single loop within.
CS106B Big O and Asymptotic Analysis
N Vs Log N Complexity With that we have $\log^2n =\log n * \log n \geq \log n$ (since $\log n \geq 1$). Specifically, it indicates that the time. With that we have $\log^2n =\log n * \log n \geq \log n$ (since $\log n \geq 1$). So yes in terms of complexity $\mathcal{o}(\log{}n)$ is faster. $$ dividing through by $\log(n^n)$ yields $$. The notation o (log n) represents logarithmic time complexity in algorithm analysis. I am wondering if this time complexity difference between n log n and n are significant in real life. When the input size is reduced by half, maybe when iterating, handling recursion, or whatsoever, it is a logarithmic time complexity (o(log n)). This order of time complexity can be seen in cases where an n * n matrix needs to be sorted along the rows. It is a mistake when taken in the context that o(n) and o(n log n) functions have better complexity than o(1) and o(log n). We understand the logarithmic aspect of time complexity and we understand n*log(n)’s relation to linear time complexity,. A quick select on finding kth element in an. When you have a single loop within.
From dzone.com
Learning Big O Notation With O(n) Complexity DZone N Vs Log N Complexity This order of time complexity can be seen in cases where an n * n matrix needs to be sorted along the rows. When the input size is reduced by half, maybe when iterating, handling recursion, or whatsoever, it is a logarithmic time complexity (o(log n)). When you have a single loop within. With that we have $\log^2n =\log n. N Vs Log N Complexity.
From www.happycoders.eu
Big O Notation and Time Complexity Easily Explained N Vs Log N Complexity Specifically, it indicates that the time. This order of time complexity can be seen in cases where an n * n matrix needs to be sorted along the rows. $$ dividing through by $\log(n^n)$ yields $$. A quick select on finding kth element in an. I am wondering if this time complexity difference between n log n and n are. N Vs Log N Complexity.
From www.youtube.com
O(n log n) Algorithm for Counting Inversions 1 Algorithm YouTube N Vs Log N Complexity When the input size is reduced by half, maybe when iterating, handling recursion, or whatsoever, it is a logarithmic time complexity (o(log n)). Specifically, it indicates that the time. When you have a single loop within. The notation o (log n) represents logarithmic time complexity in algorithm analysis. This order of time complexity can be seen in cases where an. N Vs Log N Complexity.
From www.youtube.com
Analysis of Binary Search Algorithm Time complexity of Binary Search N Vs Log N Complexity It is a mistake when taken in the context that o(n) and o(n log n) functions have better complexity than o(1) and o(log n). $$ dividing through by $\log(n^n)$ yields $$. The notation o (log n) represents logarithmic time complexity in algorithm analysis. I am wondering if this time complexity difference between n log n and n are significant in. N Vs Log N Complexity.
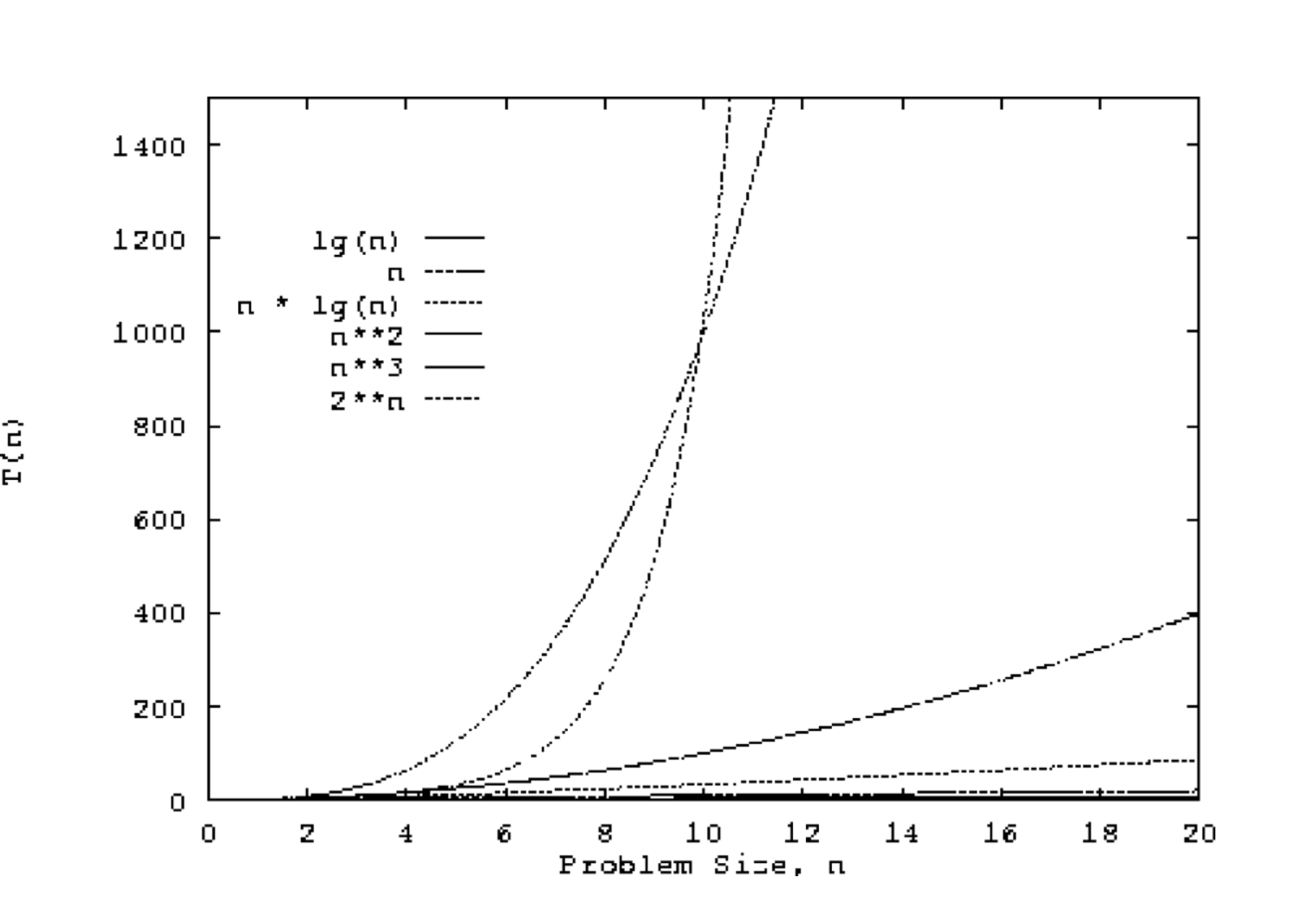
From science.slc.edu
Running Time Graphs N Vs Log N Complexity We understand the logarithmic aspect of time complexity and we understand n*log(n)’s relation to linear time complexity,. A quick select on finding kth element in an. This order of time complexity can be seen in cases where an n * n matrix needs to be sorted along the rows. Specifically, it indicates that the time. When the input size is. N Vs Log N Complexity.
From www.youtube.com
Is complexity O(log(n)) equivalent to O(sqrt(n))? YouTube N Vs Log N Complexity $$ dividing through by $\log(n^n)$ yields $$. The notation o (log n) represents logarithmic time complexity in algorithm analysis. When you have a single loop within. Specifically, it indicates that the time. So yes in terms of complexity $\mathcal{o}(\log{}n)$ is faster. With that we have $\log^2n =\log n * \log n \geq \log n$ (since $\log n \geq 1$). A. N Vs Log N Complexity.
From stackoverflow.com
language agnostic O(N log N) Complexity Similar to linear? Stack N Vs Log N Complexity The notation o (log n) represents logarithmic time complexity in algorithm analysis. Specifically, it indicates that the time. This order of time complexity can be seen in cases where an n * n matrix needs to be sorted along the rows. $$ dividing through by $\log(n^n)$ yields $$. We understand the logarithmic aspect of time complexity and we understand n*log(n)’s. N Vs Log N Complexity.
From www.youtube.com
Big O Notation Series 5 O (n log n) explained for beginners YouTube N Vs Log N Complexity I am wondering if this time complexity difference between n log n and n are significant in real life. Specifically, it indicates that the time. When you have a single loop within. The notation o (log n) represents logarithmic time complexity in algorithm analysis. It is a mistake when taken in the context that o(n) and o(n log n) functions. N Vs Log N Complexity.
From science.slc.edu
Running Time Graphs N Vs Log N Complexity When you have a single loop within. A quick select on finding kth element in an. I am wondering if this time complexity difference between n log n and n are significant in real life. When the input size is reduced by half, maybe when iterating, handling recursion, or whatsoever, it is a logarithmic time complexity (o(log n)). This order. N Vs Log N Complexity.
From web.stanford.edu
CS106B Big O and Asymptotic Analysis N Vs Log N Complexity This order of time complexity can be seen in cases where an n * n matrix needs to be sorted along the rows. So yes in terms of complexity $\mathcal{o}(\log{}n)$ is faster. We understand the logarithmic aspect of time complexity and we understand n*log(n)’s relation to linear time complexity,. I am wondering if this time complexity difference between n log. N Vs Log N Complexity.
From www.pinterest.com
Linear Time vs. Logarithmic Time — Big O Notation Big o notation N Vs Log N Complexity A quick select on finding kth element in an. We understand the logarithmic aspect of time complexity and we understand n*log(n)’s relation to linear time complexity,. The notation o (log n) represents logarithmic time complexity in algorithm analysis. I am wondering if this time complexity difference between n log n and n are significant in real life. $$ dividing through. N Vs Log N Complexity.
From paulonteri.com
Complexity Analysis & Big O DSA N Vs Log N Complexity It is a mistake when taken in the context that o(n) and o(n log n) functions have better complexity than o(1) and o(log n). We understand the logarithmic aspect of time complexity and we understand n*log(n)’s relation to linear time complexity,. $$ dividing through by $\log(n^n)$ yields $$. With that we have $\log^2n =\log n * \log n \geq \log. N Vs Log N Complexity.
From medium.com
Time Complexity A Simple Explanation (with Code Examples) by Brahim N Vs Log N Complexity The notation o (log n) represents logarithmic time complexity in algorithm analysis. A quick select on finding kth element in an. When the input size is reduced by half, maybe when iterating, handling recursion, or whatsoever, it is a logarithmic time complexity (o(log n)). Specifically, it indicates that the time. This order of time complexity can be seen in cases. N Vs Log N Complexity.
From morioh.com
Algorithms Explained Computational Complexity N Vs Log N Complexity A quick select on finding kth element in an. When the input size is reduced by half, maybe when iterating, handling recursion, or whatsoever, it is a logarithmic time complexity (o(log n)). It is a mistake when taken in the context that o(n) and o(n log n) functions have better complexity than o(1) and o(log n). $$ dividing through by. N Vs Log N Complexity.
From mavink.com
Complexities Of Sorting Algorithms N Vs Log N Complexity A quick select on finding kth element in an. When you have a single loop within. With that we have $\log^2n =\log n * \log n \geq \log n$ (since $\log n \geq 1$). The notation o (log n) represents logarithmic time complexity in algorithm analysis. This order of time complexity can be seen in cases where an n *. N Vs Log N Complexity.
From quizlet.com
Time Complexity Diagram Quizlet N Vs Log N Complexity So yes in terms of complexity $\mathcal{o}(\log{}n)$ is faster. The notation o (log n) represents logarithmic time complexity in algorithm analysis. I am wondering if this time complexity difference between n log n and n are significant in real life. With that we have $\log^2n =\log n * \log n \geq \log n$ (since $\log n \geq 1$). This order. N Vs Log N Complexity.
From askcodes.net
Big O confusion log2(N) vs log3(N) Ask Codes N Vs Log N Complexity When the input size is reduced by half, maybe when iterating, handling recursion, or whatsoever, it is a logarithmic time complexity (o(log n)). This order of time complexity can be seen in cases where an n * n matrix needs to be sorted along the rows. I am wondering if this time complexity difference between n log n and n. N Vs Log N Complexity.
From learn2torials.com
Part5 Logarithmic Time Complexity O(log n) N Vs Log N Complexity $$ dividing through by $\log(n^n)$ yields $$. It is a mistake when taken in the context that o(n) and o(n log n) functions have better complexity than o(1) and o(log n). The notation o (log n) represents logarithmic time complexity in algorithm analysis. This order of time complexity can be seen in cases where an n * n matrix needs. N Vs Log N Complexity.
From www.slideshare.net
Time complexity N Vs Log N Complexity So yes in terms of complexity $\mathcal{o}(\log{}n)$ is faster. It is a mistake when taken in the context that o(n) and o(n log n) functions have better complexity than o(1) and o(log n). Specifically, it indicates that the time. With that we have $\log^2n =\log n * \log n \geq \log n$ (since $\log n \geq 1$). A quick select. N Vs Log N Complexity.
From www.csubc.com
Lecture 5 predicate logic CPSC N Vs Log N Complexity With that we have $\log^2n =\log n * \log n \geq \log n$ (since $\log n \geq 1$). Specifically, it indicates that the time. When the input size is reduced by half, maybe when iterating, handling recursion, or whatsoever, it is a logarithmic time complexity (o(log n)). This order of time complexity can be seen in cases where an n. N Vs Log N Complexity.
From erotourtes.github.io
Data structures and algorithms Knowledge Base N Vs Log N Complexity When you have a single loop within. With that we have $\log^2n =\log n * \log n \geq \log n$ (since $\log n \geq 1$). This order of time complexity can be seen in cases where an n * n matrix needs to be sorted along the rows. So yes in terms of complexity $\mathcal{o}(\log{}n)$ is faster. Specifically, it indicates. N Vs Log N Complexity.
From www.reddit.com
Can anyone explain why this function has a time complexity of O(logn N Vs Log N Complexity Specifically, it indicates that the time. With that we have $\log^2n =\log n * \log n \geq \log n$ (since $\log n \geq 1$). I am wondering if this time complexity difference between n log n and n are significant in real life. $$ dividing through by $\log(n^n)$ yields $$. When the input size is reduced by half, maybe when. N Vs Log N Complexity.
From www.youtube.com
Big O(Log N) Logarithmic Time Complexity Binary Search Algorithm N Vs Log N Complexity The notation o (log n) represents logarithmic time complexity in algorithm analysis. We understand the logarithmic aspect of time complexity and we understand n*log(n)’s relation to linear time complexity,. Specifically, it indicates that the time. This order of time complexity can be seen in cases where an n * n matrix needs to be sorted along the rows. A quick. N Vs Log N Complexity.
From www.youtube.com
Why does log(N) appear so frequently in Complexity Analysis? YouTube N Vs Log N Complexity So yes in terms of complexity $\mathcal{o}(\log{}n)$ is faster. When the input size is reduced by half, maybe when iterating, handling recursion, or whatsoever, it is a logarithmic time complexity (o(log n)). When you have a single loop within. A quick select on finding kth element in an. The notation o (log n) represents logarithmic time complexity in algorithm analysis.. N Vs Log N Complexity.
From skaylab.com
Exercices fonctions logarithmes Terminales C&D SkayLab N Vs Log N Complexity $$ dividing through by $\log(n^n)$ yields $$. This order of time complexity can be seen in cases where an n * n matrix needs to be sorted along the rows. Specifically, it indicates that the time. It is a mistake when taken in the context that o(n) and o(n log n) functions have better complexity than o(1) and o(log n).. N Vs Log N Complexity.
From chart-studio.plotly.com
logn, 2logn, nlogn, 2nlogn, n(logn)^2, 2n(logn)^2, n log(logn), 2n log N Vs Log N Complexity This order of time complexity can be seen in cases where an n * n matrix needs to be sorted along the rows. The notation o (log n) represents logarithmic time complexity in algorithm analysis. Specifically, it indicates that the time. It is a mistake when taken in the context that o(n) and o(n log n) functions have better complexity. N Vs Log N Complexity.
From thetapacademy.com
Time & Space Complexity in Data Structures The TAP Academy N Vs Log N Complexity It is a mistake when taken in the context that o(n) and o(n log n) functions have better complexity than o(1) and o(log n). When you have a single loop within. So yes in terms of complexity $\mathcal{o}(\log{}n)$ is faster. With that we have $\log^2n =\log n * \log n \geq \log n$ (since $\log n \geq 1$). Specifically, it. N Vs Log N Complexity.
From www.geeksforgeeks.org
What is Logarithmic Time Complexity? A Complete Tutorial N Vs Log N Complexity $$ dividing through by $\log(n^n)$ yields $$. It is a mistake when taken in the context that o(n) and o(n log n) functions have better complexity than o(1) and o(log n). Specifically, it indicates that the time. With that we have $\log^2n =\log n * \log n \geq \log n$ (since $\log n \geq 1$). When you have a single. N Vs Log N Complexity.
From science.slc.edu
Running Time Graphs N Vs Log N Complexity It is a mistake when taken in the context that o(n) and o(n log n) functions have better complexity than o(1) and o(log n). When you have a single loop within. This order of time complexity can be seen in cases where an n * n matrix needs to be sorted along the rows. The notation o (log n) represents. N Vs Log N Complexity.
From dev.to
What is the logarithmic runtime O(log(n))? DEV Community N Vs Log N Complexity I am wondering if this time complexity difference between n log n and n are significant in real life. Specifically, it indicates that the time. $$ dividing through by $\log(n^n)$ yields $$. A quick select on finding kth element in an. This order of time complexity can be seen in cases where an n * n matrix needs to be. N Vs Log N Complexity.
From learn2torials.com
Part5 Logarithmic Time Complexity O(log n) N Vs Log N Complexity $$ dividing through by $\log(n^n)$ yields $$. I am wondering if this time complexity difference between n log n and n are significant in real life. With that we have $\log^2n =\log n * \log n \geq \log n$ (since $\log n \geq 1$). So yes in terms of complexity $\mathcal{o}(\log{}n)$ is faster. When you have a single loop within.. N Vs Log N Complexity.
From www.youtube.com
Analysis of Quick Sort Algorithm Time complexity of Quick Sort N Vs Log N Complexity When the input size is reduced by half, maybe when iterating, handling recursion, or whatsoever, it is a logarithmic time complexity (o(log n)). It is a mistake when taken in the context that o(n) and o(n log n) functions have better complexity than o(1) and o(log n). This order of time complexity can be seen in cases where an n. N Vs Log N Complexity.
From www.slideserve.com
PPT Sorting PowerPoint Presentation, free download ID1112947 N Vs Log N Complexity I am wondering if this time complexity difference between n log n and n are significant in real life. When the input size is reduced by half, maybe when iterating, handling recursion, or whatsoever, it is a logarithmic time complexity (o(log n)). With that we have $\log^2n =\log n * \log n \geq \log n$ (since $\log n \geq 1$).. N Vs Log N Complexity.
From daplus.net
O (log n)은 정확히 무엇을 의미합니까? 리뷰나라 N Vs Log N Complexity When the input size is reduced by half, maybe when iterating, handling recursion, or whatsoever, it is a logarithmic time complexity (o(log n)). A quick select on finding kth element in an. It is a mistake when taken in the context that o(n) and o(n log n) functions have better complexity than o(1) and o(log n). So yes in terms. N Vs Log N Complexity.
From exchangetuts.com
Is complexity O(log(n)) equivalent to O(sqrt(n))? N Vs Log N Complexity The notation o (log n) represents logarithmic time complexity in algorithm analysis. $$ dividing through by $\log(n^n)$ yields $$. It is a mistake when taken in the context that o(n) and o(n log n) functions have better complexity than o(1) and o(log n). We understand the logarithmic aspect of time complexity and we understand n*log(n)’s relation to linear time complexity,.. N Vs Log N Complexity.