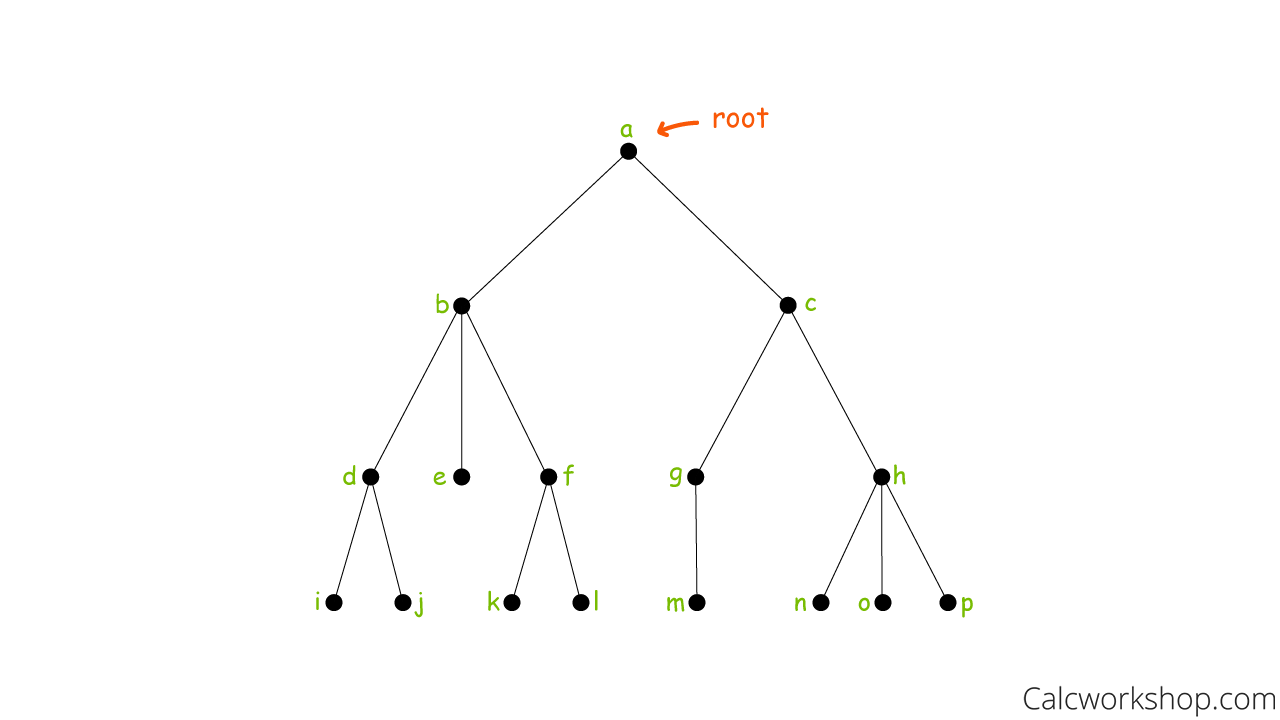
Tree Graph Cycle . A simple connected graph is. X3.1 presents some standard characterizations and properties of trees. So a forest is a. Some examples are shown in figure 12.237. Today we’ll talk about a very special class of graphs called trees. A forest is a disjoint union of trees. in this lecture, we introduce trees and discuss some basic related properties. in this theory, a tree is defined as an undirected graph without any cycles or loops. Adding edge bj to graph t creates cycle ( b , c , i , j ). Trees arise in all sorts of applications and you’ll see them in just about every. graph theory { lecture 4: A tree is a connected graph that has no cycles. It explores the properties and. for example, if you add an edge to a tree graph between any two existing vertices, you will create a cycle, and the resulting graph is no longer a tree.
from calcworkshop.com
It explores the properties and. A simple connected graph is. A tree is a connected graph that has no cycles. in this lecture, we introduce trees and discuss some basic related properties. Some examples are shown in figure 12.237. in this theory, a tree is defined as an undirected graph without any cycles or loops. X3.1 presents some standard characterizations and properties of trees. for example, if you add an edge to a tree graph between any two existing vertices, you will create a cycle, and the resulting graph is no longer a tree. Trees arise in all sorts of applications and you’ll see them in just about every. Today we’ll talk about a very special class of graphs called trees.
Tree Graph (How To w/ 11+ StepbyStep Examples!)
Tree Graph Cycle in this lecture, we introduce trees and discuss some basic related properties. Adding edge bj to graph t creates cycle ( b , c , i , j ). So a forest is a. for example, if you add an edge to a tree graph between any two existing vertices, you will create a cycle, and the resulting graph is no longer a tree. X3.1 presents some standard characterizations and properties of trees. It explores the properties and. Today we’ll talk about a very special class of graphs called trees. A forest is a disjoint union of trees. Trees arise in all sorts of applications and you’ll see them in just about every. graph theory { lecture 4: A simple connected graph is. A tree is a connected graph that has no cycles. in this lecture, we introduce trees and discuss some basic related properties. Some examples are shown in figure 12.237. in this theory, a tree is defined as an undirected graph without any cycles or loops.
From calcworkshop.com
Tree Graph (How To w/ 11+ StepbyStep Examples!) Tree Graph Cycle in this lecture, we introduce trees and discuss some basic related properties. graph theory { lecture 4: Some examples are shown in figure 12.237. Adding edge bj to graph t creates cycle ( b , c , i , j ). A forest is a disjoint union of trees. for example, if you add an edge to. Tree Graph Cycle.
From learningzonesurinamecaj.z14.web.core.windows.net
Plant Diagram For Kids Tree Graph Cycle A tree is a connected graph that has no cycles. So a forest is a. Adding edge bj to graph t creates cycle ( b , c , i , j ). X3.1 presents some standard characterizations and properties of trees. A forest is a disjoint union of trees. for example, if you add an edge to a tree. Tree Graph Cycle.
From stackoverflow.com
Undirected graph conversion to tree Stack Overflow Tree Graph Cycle Adding edge bj to graph t creates cycle ( b , c , i , j ). Trees arise in all sorts of applications and you’ll see them in just about every. So a forest is a. Some examples are shown in figure 12.237. in this theory, a tree is defined as an undirected graph without any cycles or. Tree Graph Cycle.
From www.slideserve.com
PPT Minimum Spanning Trees Featuring Disjoint Sets PowerPoint Presentation ID9513962 Tree Graph Cycle Today we’ll talk about a very special class of graphs called trees. Trees arise in all sorts of applications and you’ll see them in just about every. It explores the properties and. for example, if you add an edge to a tree graph between any two existing vertices, you will create a cycle, and the resulting graph is no. Tree Graph Cycle.
From www.mdpi.com
Mathematics Free FullText Constructing an Evolutionary Tree and PathCycle Graph Evolution Tree Graph Cycle So a forest is a. Some examples are shown in figure 12.237. Adding edge bj to graph t creates cycle ( b , c , i , j ). X3.1 presents some standard characterizations and properties of trees. A tree is a connected graph that has no cycles. It explores the properties and. A forest is a disjoint union of. Tree Graph Cycle.
From mavink.com
Forest Graph Theory Tree Graph Cycle Adding edge bj to graph t creates cycle ( b , c , i , j ). Trees arise in all sorts of applications and you’ll see them in just about every. in this theory, a tree is defined as an undirected graph without any cycles or loops. graph theory { lecture 4: for example, if you. Tree Graph Cycle.
From mavink.com
Graph Theory Tree Tree Graph Cycle A forest is a disjoint union of trees. So a forest is a. Adding edge bj to graph t creates cycle ( b , c , i , j ). A tree is a connected graph that has no cycles. in this lecture, we introduce trees and discuss some basic related properties. A simple connected graph is. graph. Tree Graph Cycle.
From www.prepbytes.com
Graph Tree PrepBytes Blog Tree Graph Cycle A simple connected graph is. So a forest is a. graph theory { lecture 4: in this lecture, we introduce trees and discuss some basic related properties. Trees arise in all sorts of applications and you’ll see them in just about every. Today we’ll talk about a very special class of graphs called trees. for example, if. Tree Graph Cycle.
From www.vectorstock.com
Infographic plant growth stages tree Royalty Free Vector Tree Graph Cycle Today we’ll talk about a very special class of graphs called trees. Trees arise in all sorts of applications and you’ll see them in just about every. for example, if you add an edge to a tree graph between any two existing vertices, you will create a cycle, and the resulting graph is no longer a tree. It explores. Tree Graph Cycle.
From mavink.com
Graph Theory Tree Tree Graph Cycle It explores the properties and. A simple connected graph is. Today we’ll talk about a very special class of graphs called trees. in this lecture, we introduce trees and discuss some basic related properties. Trees arise in all sorts of applications and you’ll see them in just about every. graph theory { lecture 4: for example, if. Tree Graph Cycle.
From www.youtube.com
Identifying Isomorphic Trees Graph Theory YouTube Tree Graph Cycle So a forest is a. A forest is a disjoint union of trees. in this lecture, we introduce trees and discuss some basic related properties. Today we’ll talk about a very special class of graphs called trees. Adding edge bj to graph t creates cycle ( b , c , i , j ). Some examples are shown in. Tree Graph Cycle.
From slides.com
Introduction to Trees and Graphs Tree Graph Cycle Some examples are shown in figure 12.237. X3.1 presents some standard characterizations and properties of trees. Today we’ll talk about a very special class of graphs called trees. in this theory, a tree is defined as an undirected graph without any cycles or loops. A tree is a connected graph that has no cycles. Trees arise in all sorts. Tree Graph Cycle.
From www.interviewkickstart.com
Graph Theory Trees Tree Graph Cycle It explores the properties and. Adding edge bj to graph t creates cycle ( b , c , i , j ). A simple connected graph is. Some examples are shown in figure 12.237. X3.1 presents some standard characterizations and properties of trees. in this theory, a tree is defined as an undirected graph without any cycles or loops.. Tree Graph Cycle.
From www.youtube.com
Intro to Tree Graphs Trees in Graph Theory, Equivalent Definitions YouTube Tree Graph Cycle X3.1 presents some standard characterizations and properties of trees. graph theory { lecture 4: for example, if you add an edge to a tree graph between any two existing vertices, you will create a cycle, and the resulting graph is no longer a tree. in this lecture, we introduce trees and discuss some basic related properties. A. Tree Graph Cycle.
From www.youtube.com
Tree center(s) Graph Theory YouTube Tree Graph Cycle X3.1 presents some standard characterizations and properties of trees. Some examples are shown in figure 12.237. A simple connected graph is. Trees arise in all sorts of applications and you’ll see them in just about every. for example, if you add an edge to a tree graph between any two existing vertices, you will create a cycle, and the. Tree Graph Cycle.
From slides.com
Introduction to Trees and Graphs Tree Graph Cycle X3.1 presents some standard characterizations and properties of trees. A simple connected graph is. A forest is a disjoint union of trees. graph theory { lecture 4: Adding edge bj to graph t creates cycle ( b , c , i , j ). for example, if you add an edge to a tree graph between any two. Tree Graph Cycle.
From calcworkshop.com
Tree Graph (How To w/ 11+ StepbyStep Examples!) Tree Graph Cycle A tree is a connected graph that has no cycles. So a forest is a. X3.1 presents some standard characterizations and properties of trees. Adding edge bj to graph t creates cycle ( b , c , i , j ). graph theory { lecture 4: Some examples are shown in figure 12.237. A forest is a disjoint union. Tree Graph Cycle.
From www.investopedia.com
Tree Diagram Definition Tree Graph Cycle It explores the properties and. graph theory { lecture 4: Trees arise in all sorts of applications and you’ll see them in just about every. for example, if you add an edge to a tree graph between any two existing vertices, you will create a cycle, and the resulting graph is no longer a tree. Today we’ll talk. Tree Graph Cycle.
From projectopenletter.com
Simple Tree Diagram Examples Printable Form, Templates and Letter Tree Graph Cycle graph theory { lecture 4: So a forest is a. It explores the properties and. A tree is a connected graph that has no cycles. A simple connected graph is. X3.1 presents some standard characterizations and properties of trees. A forest is a disjoint union of trees. in this lecture, we introduce trees and discuss some basic related. Tree Graph Cycle.
From www.dreamstime.com
Tree Graph And Check Mark Cycle Illustration Stock Illustration Illustration of business, cube Tree Graph Cycle Today we’ll talk about a very special class of graphs called trees. Adding edge bj to graph t creates cycle ( b , c , i , j ). in this theory, a tree is defined as an undirected graph without any cycles or loops. A tree is a connected graph that has no cycles. Some examples are shown. Tree Graph Cycle.
From ptwiddle.github.io
Lecture 6 Trees Tree Graph Cycle Some examples are shown in figure 12.237. A tree is a connected graph that has no cycles. in this lecture, we introduce trees and discuss some basic related properties. graph theory { lecture 4: A simple connected graph is. X3.1 presents some standard characterizations and properties of trees. for example, if you add an edge to a. Tree Graph Cycle.
From www.youtube.com
Tree (graph theory) YouTube Tree Graph Cycle graph theory { lecture 4: in this theory, a tree is defined as an undirected graph without any cycles or loops. in this lecture, we introduce trees and discuss some basic related properties. A simple connected graph is. Trees arise in all sorts of applications and you’ll see them in just about every. for example, if. Tree Graph Cycle.
From www.youtube.com
Rooting a tree Graph Theory YouTube Tree Graph Cycle X3.1 presents some standard characterizations and properties of trees. Trees arise in all sorts of applications and you’ll see them in just about every. So a forest is a. in this lecture, we introduce trees and discuss some basic related properties. for example, if you add an edge to a tree graph between any two existing vertices, you. Tree Graph Cycle.
From www.pinterest.com
the tree life cycle is shown in this graphic Tree Graph Cycle X3.1 presents some standard characterizations and properties of trees. So a forest is a. Some examples are shown in figure 12.237. in this lecture, we introduce trees and discuss some basic related properties. in this theory, a tree is defined as an undirected graph without any cycles or loops. Adding edge bj to graph t creates cycle (. Tree Graph Cycle.
From corporatefinanceinstitute.com
Tree Diagram Definition, Event Types, Calculating Probabilities Tree Graph Cycle X3.1 presents some standard characterizations and properties of trees. Some examples are shown in figure 12.237. graph theory { lecture 4: for example, if you add an edge to a tree graph between any two existing vertices, you will create a cycle, and the resulting graph is no longer a tree. Today we’ll talk about a very special. Tree Graph Cycle.
From www.jointjs.com
Tree graph and cycles Demo applications & examples Tree Graph Cycle A tree is a connected graph that has no cycles. X3.1 presents some standard characterizations and properties of trees. It explores the properties and. Trees arise in all sorts of applications and you’ll see them in just about every. A simple connected graph is. in this lecture, we introduce trees and discuss some basic related properties. in this. Tree Graph Cycle.
From www.researchgate.net
Example of spanning tree. G corresponds to a graph where all cycles are... Download Scientific Tree Graph Cycle graph theory { lecture 4: So a forest is a. in this lecture, we introduce trees and discuss some basic related properties. Some examples are shown in figure 12.237. for example, if you add an edge to a tree graph between any two existing vertices, you will create a cycle, and the resulting graph is no longer. Tree Graph Cycle.
From math.stackexchange.com
Define A Graph Tree Graph With "Cycles" as Nodes Mathematics Stack Exchange Tree Graph Cycle for example, if you add an edge to a tree graph between any two existing vertices, you will create a cycle, and the resulting graph is no longer a tree. Adding edge bj to graph t creates cycle ( b , c , i , j ). in this lecture, we introduce trees and discuss some basic related. Tree Graph Cycle.
From www.slideserve.com
PPT Lecture 32 Graph TRAVERSALS PowerPoint Presentation, free download ID2608133 Tree Graph Cycle Today we’ll talk about a very special class of graphs called trees. for example, if you add an edge to a tree graph between any two existing vertices, you will create a cycle, and the resulting graph is no longer a tree. in this theory, a tree is defined as an undirected graph without any cycles or loops.. Tree Graph Cycle.
From courses.cs.washington.edu
Trees as Graphs Tree Graph Cycle graph theory { lecture 4: in this lecture, we introduce trees and discuss some basic related properties. Some examples are shown in figure 12.237. It explores the properties and. in this theory, a tree is defined as an undirected graph without any cycles or loops. A simple connected graph is. for example, if you add an. Tree Graph Cycle.
From www.slideserve.com
PPT Trees and Cycles. PowerPoint Presentation, free download ID1800921 Tree Graph Cycle A tree is a connected graph that has no cycles. in this lecture, we introduce trees and discuss some basic related properties. It explores the properties and. for example, if you add an edge to a tree graph between any two existing vertices, you will create a cycle, and the resulting graph is no longer a tree. Trees. Tree Graph Cycle.
From www.dreamstime.com
A Growth Cycle of a Longan Tree on a White Background. Stock Vector Illustration of diagram Tree Graph Cycle in this lecture, we introduce trees and discuss some basic related properties. graph theory { lecture 4: Trees arise in all sorts of applications and you’ll see them in just about every. A forest is a disjoint union of trees. A simple connected graph is. So a forest is a. Some examples are shown in figure 12.237. A. Tree Graph Cycle.
From www.sexizpix.com
Tree Life Cycle Free Presentation Template Piktochart Sexiz Pix Tree Graph Cycle Adding edge bj to graph t creates cycle ( b , c , i , j ). A simple connected graph is. A tree is a connected graph that has no cycles. in this lecture, we introduce trees and discuss some basic related properties. in this theory, a tree is defined as an undirected graph without any cycles. Tree Graph Cycle.
From math.stackexchange.com
Define A Graph Tree Graph With "Cycles" as Nodes Mathematics Stack Exchange Tree Graph Cycle in this lecture, we introduce trees and discuss some basic related properties. A forest is a disjoint union of trees. graph theory { lecture 4: in this theory, a tree is defined as an undirected graph without any cycles or loops. Trees arise in all sorts of applications and you’ll see them in just about every. Today. Tree Graph Cycle.
From aznswerzonenun.z21.web.core.windows.net
Tree Life Cycle Printable Tree Graph Cycle Today we’ll talk about a very special class of graphs called trees. Trees arise in all sorts of applications and you’ll see them in just about every. in this lecture, we introduce trees and discuss some basic related properties. So a forest is a. A simple connected graph is. A forest is a disjoint union of trees. A tree. Tree Graph Cycle.