Thresholds Versus Fractional Expectation-Thresholds . For an increasing family ℱ {\mathcal {f}} on a finite set 𝑋 x, we write (with definitions below) subscript 𝑝 𝑐 ℱ p_ {c} ( {\mathcal {f}}), subscript 𝑞 𝑓 ℱ q_ {f}. $p_c \mathcal(f) = o(q_f (\mathcal{f}) \mathrm{log}\ell (\mathcal{f})$ for any increasing family $\mathcal{f}$ on a finite set $x$, where. Proving a conjecture of talagrand, a fractional version of the. For an increasing family f on a finite set x, we write (with definitions below) pc(f), qf(f) and `(f) for the threshold, fractional expectation.
from www.studocu.com
Proving a conjecture of talagrand, a fractional version of the. For an increasing family f on a finite set x, we write (with definitions below) pc(f), qf(f) and `(f) for the threshold, fractional expectation. For an increasing family ℱ {\mathcal {f}} on a finite set 𝑋 x, we write (with definitions below) subscript 𝑝 𝑐 ℱ p_ {c} ( {\mathcal {f}}), subscript 𝑞 𝑓 ℱ q_ {f}. $p_c \mathcal(f) = o(q_f (\mathcal{f}) \mathrm{log}\ell (\mathcal{f})$ for any increasing family $\mathcal{f}$ on a finite set $x$, where.
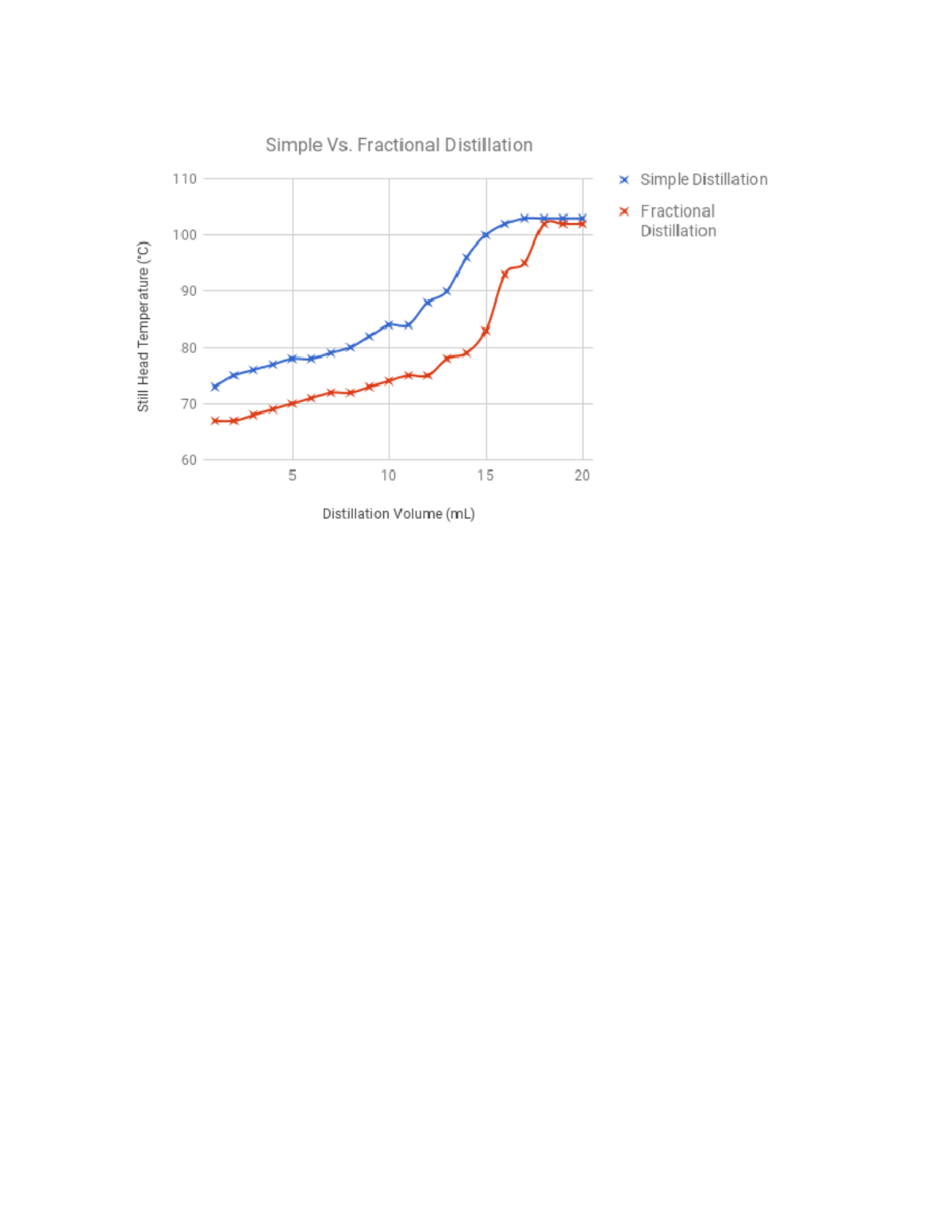
Lab 1 Report Simple vs. Fractional Distillation Results and
Thresholds Versus Fractional Expectation-Thresholds For an increasing family ℱ {\mathcal {f}} on a finite set 𝑋 x, we write (with definitions below) subscript 𝑝 𝑐 ℱ p_ {c} ( {\mathcal {f}}), subscript 𝑞 𝑓 ℱ q_ {f}. $p_c \mathcal(f) = o(q_f (\mathcal{f}) \mathrm{log}\ell (\mathcal{f})$ for any increasing family $\mathcal{f}$ on a finite set $x$, where. For an increasing family f on a finite set x, we write (with definitions below) pc(f), qf(f) and `(f) for the threshold, fractional expectation. Proving a conjecture of talagrand, a fractional version of the. For an increasing family ℱ {\mathcal {f}} on a finite set 𝑋 x, we write (with definitions below) subscript 𝑝 𝑐 ℱ p_ {c} ( {\mathcal {f}}), subscript 𝑞 𝑓 ℱ q_ {f}.
From www.researchgate.net
Fraction skill score (FSS) with different thresholds for Thresholds Versus Fractional Expectation-Thresholds $p_c \mathcal(f) = o(q_f (\mathcal{f}) \mathrm{log}\ell (\mathcal{f})$ for any increasing family $\mathcal{f}$ on a finite set $x$, where. For an increasing family f on a finite set x, we write (with definitions below) pc(f), qf(f) and `(f) for the threshold, fractional expectation. Proving a conjecture of talagrand, a fractional version of the. For an increasing family ℱ {\mathcal {f}} on. Thresholds Versus Fractional Expectation-Thresholds.
From www.researchgate.net
Trajectory projection of fractionalorder fronts depending of the Thresholds Versus Fractional Expectation-Thresholds For an increasing family ℱ {\mathcal {f}} on a finite set 𝑋 x, we write (with definitions below) subscript 𝑝 𝑐 ℱ p_ {c} ( {\mathcal {f}}), subscript 𝑞 𝑓 ℱ q_ {f}. $p_c \mathcal(f) = o(q_f (\mathcal{f}) \mathrm{log}\ell (\mathcal{f})$ for any increasing family $\mathcal{f}$ on a finite set $x$, where. For an increasing family f on a finite set. Thresholds Versus Fractional Expectation-Thresholds.
From www.ahajournals.org
Revisiting the Optimal Fractional Flow Reserve and Instantaneous Wave Thresholds Versus Fractional Expectation-Thresholds $p_c \mathcal(f) = o(q_f (\mathcal{f}) \mathrm{log}\ell (\mathcal{f})$ for any increasing family $\mathcal{f}$ on a finite set $x$, where. For an increasing family f on a finite set x, we write (with definitions below) pc(f), qf(f) and `(f) for the threshold, fractional expectation. Proving a conjecture of talagrand, a fractional version of the. For an increasing family ℱ {\mathcal {f}} on. Thresholds Versus Fractional Expectation-Thresholds.
From gpnotebook.com
Classification of heart failure based on ejection fraction HF pef Thresholds Versus Fractional Expectation-Thresholds For an increasing family ℱ {\mathcal {f}} on a finite set 𝑋 x, we write (with definitions below) subscript 𝑝 𝑐 ℱ p_ {c} ( {\mathcal {f}}), subscript 𝑞 𝑓 ℱ q_ {f}. Proving a conjecture of talagrand, a fractional version of the. $p_c \mathcal(f) = o(q_f (\mathcal{f}) \mathrm{log}\ell (\mathcal{f})$ for any increasing family $\mathcal{f}$ on a finite set $x$,. Thresholds Versus Fractional Expectation-Thresholds.
From www.researchgate.net
SVM's best threshold vs. Malicious Nodes percentage In our simulations Thresholds Versus Fractional Expectation-Thresholds For an increasing family ℱ {\mathcal {f}} on a finite set 𝑋 x, we write (with definitions below) subscript 𝑝 𝑐 ℱ p_ {c} ( {\mathcal {f}}), subscript 𝑞 𝑓 ℱ q_ {f}. $p_c \mathcal(f) = o(q_f (\mathcal{f}) \mathrm{log}\ell (\mathcal{f})$ for any increasing family $\mathcal{f}$ on a finite set $x$, where. For an increasing family f on a finite set. Thresholds Versus Fractional Expectation-Thresholds.
From www.researchgate.net
(a) Scatter fraction versus source position for no septa, 0.15and Thresholds Versus Fractional Expectation-Thresholds $p_c \mathcal(f) = o(q_f (\mathcal{f}) \mathrm{log}\ell (\mathcal{f})$ for any increasing family $\mathcal{f}$ on a finite set $x$, where. For an increasing family f on a finite set x, we write (with definitions below) pc(f), qf(f) and `(f) for the threshold, fractional expectation. For an increasing family ℱ {\mathcal {f}} on a finite set 𝑋 x, we write (with definitions below). Thresholds Versus Fractional Expectation-Thresholds.
From wwwnc.cdc.gov
Figure Thresholds versus Anomaly Detection for Surveillance of Thresholds Versus Fractional Expectation-Thresholds For an increasing family ℱ {\mathcal {f}} on a finite set 𝑋 x, we write (with definitions below) subscript 𝑝 𝑐 ℱ p_ {c} ( {\mathcal {f}}), subscript 𝑞 𝑓 ℱ q_ {f}. $p_c \mathcal(f) = o(q_f (\mathcal{f}) \mathrm{log}\ell (\mathcal{f})$ for any increasing family $\mathcal{f}$ on a finite set $x$, where. For an increasing family f on a finite set. Thresholds Versus Fractional Expectation-Thresholds.
From www.researchgate.net
Threshold versus P fa graph generated empirically for the first five Thresholds Versus Fractional Expectation-Thresholds $p_c \mathcal(f) = o(q_f (\mathcal{f}) \mathrm{log}\ell (\mathcal{f})$ for any increasing family $\mathcal{f}$ on a finite set $x$, where. For an increasing family f on a finite set x, we write (with definitions below) pc(f), qf(f) and `(f) for the threshold, fractional expectation. Proving a conjecture of talagrand, a fractional version of the. For an increasing family ℱ {\mathcal {f}} on. Thresholds Versus Fractional Expectation-Thresholds.
From www.researchgate.net
Thresholds of left ventricular ejection fraction (LVEF) and definition Thresholds Versus Fractional Expectation-Thresholds $p_c \mathcal(f) = o(q_f (\mathcal{f}) \mathrm{log}\ell (\mathcal{f})$ for any increasing family $\mathcal{f}$ on a finite set $x$, where. For an increasing family f on a finite set x, we write (with definitions below) pc(f), qf(f) and `(f) for the threshold, fractional expectation. Proving a conjecture of talagrand, a fractional version of the. For an increasing family ℱ {\mathcal {f}} on. Thresholds Versus Fractional Expectation-Thresholds.
From www.researchgate.net
6 Estimates of Observed Fraction of 1's vs Expected Fraction, by Thresholds Versus Fractional Expectation-Thresholds For an increasing family ℱ {\mathcal {f}} on a finite set 𝑋 x, we write (with definitions below) subscript 𝑝 𝑐 ℱ p_ {c} ( {\mathcal {f}}), subscript 𝑞 𝑓 ℱ q_ {f}. For an increasing family f on a finite set x, we write (with definitions below) pc(f), qf(f) and `(f) for the threshold, fractional expectation. Proving a conjecture. Thresholds Versus Fractional Expectation-Thresholds.
From www.studocu.com
Lab 1 Report Simple vs. Fractional Distillation Results and Thresholds Versus Fractional Expectation-Thresholds For an increasing family f on a finite set x, we write (with definitions below) pc(f), qf(f) and `(f) for the threshold, fractional expectation. Proving a conjecture of talagrand, a fractional version of the. $p_c \mathcal(f) = o(q_f (\mathcal{f}) \mathrm{log}\ell (\mathcal{f})$ for any increasing family $\mathcal{f}$ on a finite set $x$, where. For an increasing family ℱ {\mathcal {f}} on. Thresholds Versus Fractional Expectation-Thresholds.
From deepai.org
Thresholds versus fractional expectationthresholds DeepAI Thresholds Versus Fractional Expectation-Thresholds For an increasing family f on a finite set x, we write (with definitions below) pc(f), qf(f) and `(f) for the threshold, fractional expectation. For an increasing family ℱ {\mathcal {f}} on a finite set 𝑋 x, we write (with definitions below) subscript 𝑝 𝑐 ℱ p_ {c} ( {\mathcal {f}}), subscript 𝑞 𝑓 ℱ q_ {f}. Proving a conjecture. Thresholds Versus Fractional Expectation-Thresholds.
From www.researchgate.net
chart of expected thresholds for 16kHz. Download Scientific Diagram Thresholds Versus Fractional Expectation-Thresholds For an increasing family ℱ {\mathcal {f}} on a finite set 𝑋 x, we write (with definitions below) subscript 𝑝 𝑐 ℱ p_ {c} ( {\mathcal {f}}), subscript 𝑞 𝑓 ℱ q_ {f}. $p_c \mathcal(f) = o(q_f (\mathcal{f}) \mathrm{log}\ell (\mathcal{f})$ for any increasing family $\mathcal{f}$ on a finite set $x$, where. Proving a conjecture of talagrand, a fractional version of. Thresholds Versus Fractional Expectation-Thresholds.
From www.researchgate.net
Diversity in SBE propagation patterns. A, Spearman correlation matrices Thresholds Versus Fractional Expectation-Thresholds $p_c \mathcal(f) = o(q_f (\mathcal{f}) \mathrm{log}\ell (\mathcal{f})$ for any increasing family $\mathcal{f}$ on a finite set $x$, where. Proving a conjecture of talagrand, a fractional version of the. For an increasing family f on a finite set x, we write (with definitions below) pc(f), qf(f) and `(f) for the threshold, fractional expectation. For an increasing family ℱ {\mathcal {f}} on. Thresholds Versus Fractional Expectation-Thresholds.
From www.researchgate.net
Psychophysical Thresholds versus M Download Scientific Diagram Thresholds Versus Fractional Expectation-Thresholds Proving a conjecture of talagrand, a fractional version of the. $p_c \mathcal(f) = o(q_f (\mathcal{f}) \mathrm{log}\ell (\mathcal{f})$ for any increasing family $\mathcal{f}$ on a finite set $x$, where. For an increasing family f on a finite set x, we write (with definitions below) pc(f), qf(f) and `(f) for the threshold, fractional expectation. For an increasing family ℱ {\mathcal {f}} on. Thresholds Versus Fractional Expectation-Thresholds.
From www.researchgate.net
The fraction skill score (FSS) as a function of the different β values Thresholds Versus Fractional Expectation-Thresholds For an increasing family ℱ {\mathcal {f}} on a finite set 𝑋 x, we write (with definitions below) subscript 𝑝 𝑐 ℱ p_ {c} ( {\mathcal {f}}), subscript 𝑞 𝑓 ℱ q_ {f}. Proving a conjecture of talagrand, a fractional version of the. For an increasing family f on a finite set x, we write (with definitions below) pc(f), qf(f). Thresholds Versus Fractional Expectation-Thresholds.
From chart-studio.plotly.com
Fractional Distillation Temperature vs Volume of Distillate scatter Thresholds Versus Fractional Expectation-Thresholds For an increasing family ℱ {\mathcal {f}} on a finite set 𝑋 x, we write (with definitions below) subscript 𝑝 𝑐 ℱ p_ {c} ( {\mathcal {f}}), subscript 𝑞 𝑓 ℱ q_ {f}. Proving a conjecture of talagrand, a fractional version of the. For an increasing family f on a finite set x, we write (with definitions below) pc(f), qf(f). Thresholds Versus Fractional Expectation-Thresholds.
From www.ahajournals.org
Revisiting the Optimal Fractional Flow Reserve and Instantaneous Wave Thresholds Versus Fractional Expectation-Thresholds For an increasing family f on a finite set x, we write (with definitions below) pc(f), qf(f) and `(f) for the threshold, fractional expectation. For an increasing family ℱ {\mathcal {f}} on a finite set 𝑋 x, we write (with definitions below) subscript 𝑝 𝑐 ℱ p_ {c} ( {\mathcal {f}}), subscript 𝑞 𝑓 ℱ q_ {f}. $p_c \mathcal(f) =. Thresholds Versus Fractional Expectation-Thresholds.
From www.researchgate.net
Effect of carrying capacity on the expected thresholds x (o) for Thresholds Versus Fractional Expectation-Thresholds $p_c \mathcal(f) = o(q_f (\mathcal{f}) \mathrm{log}\ell (\mathcal{f})$ for any increasing family $\mathcal{f}$ on a finite set $x$, where. For an increasing family f on a finite set x, we write (with definitions below) pc(f), qf(f) and `(f) for the threshold, fractional expectation. Proving a conjecture of talagrand, a fractional version of the. For an increasing family ℱ {\mathcal {f}} on. Thresholds Versus Fractional Expectation-Thresholds.
From www.researchgate.net
Thresholds versus the aspect ratio for different thicknesses of Thresholds Versus Fractional Expectation-Thresholds For an increasing family f on a finite set x, we write (with definitions below) pc(f), qf(f) and `(f) for the threshold, fractional expectation. Proving a conjecture of talagrand, a fractional version of the. $p_c \mathcal(f) = o(q_f (\mathcal{f}) \mathrm{log}\ell (\mathcal{f})$ for any increasing family $\mathcal{f}$ on a finite set $x$, where. For an increasing family ℱ {\mathcal {f}} on. Thresholds Versus Fractional Expectation-Thresholds.
From www.coursehero.com
[Solved] based on the graph from simple and fractional distillation Thresholds Versus Fractional Expectation-Thresholds Proving a conjecture of talagrand, a fractional version of the. For an increasing family f on a finite set x, we write (with definitions below) pc(f), qf(f) and `(f) for the threshold, fractional expectation. For an increasing family ℱ {\mathcal {f}} on a finite set 𝑋 x, we write (with definitions below) subscript 𝑝 𝑐 ℱ p_ {c} ( {\mathcal. Thresholds Versus Fractional Expectation-Thresholds.
From stackoverflow.com
r Count values above a range of thresholds Stack Overflow Thresholds Versus Fractional Expectation-Thresholds For an increasing family f on a finite set x, we write (with definitions below) pc(f), qf(f) and `(f) for the threshold, fractional expectation. Proving a conjecture of talagrand, a fractional version of the. $p_c \mathcal(f) = o(q_f (\mathcal{f}) \mathrm{log}\ell (\mathcal{f})$ for any increasing family $\mathcal{f}$ on a finite set $x$, where. For an increasing family ℱ {\mathcal {f}} on. Thresholds Versus Fractional Expectation-Thresholds.
From www.researchgate.net
Fraction skill score (FSS) using thresholds of 0.254, 2.54, 6.35, 12.7 Thresholds Versus Fractional Expectation-Thresholds Proving a conjecture of talagrand, a fractional version of the. For an increasing family ℱ {\mathcal {f}} on a finite set 𝑋 x, we write (with definitions below) subscript 𝑝 𝑐 ℱ p_ {c} ( {\mathcal {f}}), subscript 𝑞 𝑓 ℱ q_ {f}. For an increasing family f on a finite set x, we write (with definitions below) pc(f), qf(f). Thresholds Versus Fractional Expectation-Thresholds.
From www.researchgate.net
Fraction of "early" classifications using different tp* thresholds in Thresholds Versus Fractional Expectation-Thresholds For an increasing family f on a finite set x, we write (with definitions below) pc(f), qf(f) and `(f) for the threshold, fractional expectation. $p_c \mathcal(f) = o(q_f (\mathcal{f}) \mathrm{log}\ell (\mathcal{f})$ for any increasing family $\mathcal{f}$ on a finite set $x$, where. For an increasing family ℱ {\mathcal {f}} on a finite set 𝑋 x, we write (with definitions below). Thresholds Versus Fractional Expectation-Thresholds.
From www.youtube.com
Thresholds Versus Fractional ExpectationThresholds Keith Frankston Thresholds Versus Fractional Expectation-Thresholds For an increasing family ℱ {\mathcal {f}} on a finite set 𝑋 x, we write (with definitions below) subscript 𝑝 𝑐 ℱ p_ {c} ( {\mathcal {f}}), subscript 𝑞 𝑓 ℱ q_ {f}. For an increasing family f on a finite set x, we write (with definitions below) pc(f), qf(f) and `(f) for the threshold, fractional expectation. $p_c \mathcal(f) =. Thresholds Versus Fractional Expectation-Thresholds.
From www.researchgate.net
The fractional skill score (FSS; a and b) and bias (c and d) of the Thresholds Versus Fractional Expectation-Thresholds For an increasing family ℱ {\mathcal {f}} on a finite set 𝑋 x, we write (with definitions below) subscript 𝑝 𝑐 ℱ p_ {c} ( {\mathcal {f}}), subscript 𝑞 𝑓 ℱ q_ {f}. Proving a conjecture of talagrand, a fractional version of the. $p_c \mathcal(f) = o(q_f (\mathcal{f}) \mathrm{log}\ell (\mathcal{f})$ for any increasing family $\mathcal{f}$ on a finite set $x$,. Thresholds Versus Fractional Expectation-Thresholds.
From www.researchgate.net
Schematic of the POTFGN+Period model (A) Shown is a fractional Thresholds Versus Fractional Expectation-Thresholds Proving a conjecture of talagrand, a fractional version of the. For an increasing family f on a finite set x, we write (with definitions below) pc(f), qf(f) and `(f) for the threshold, fractional expectation. For an increasing family ℱ {\mathcal {f}} on a finite set 𝑋 x, we write (with definitions below) subscript 𝑝 𝑐 ℱ p_ {c} ( {\mathcal. Thresholds Versus Fractional Expectation-Thresholds.
From www.logicmonitor.com
Static thresholds vs. dynamic thresholds Which is right for your IT Thresholds Versus Fractional Expectation-Thresholds For an increasing family ℱ {\mathcal {f}} on a finite set 𝑋 x, we write (with definitions below) subscript 𝑝 𝑐 ℱ p_ {c} ( {\mathcal {f}}), subscript 𝑞 𝑓 ℱ q_ {f}. For an increasing family f on a finite set x, we write (with definitions below) pc(f), qf(f) and `(f) for the threshold, fractional expectation. Proving a conjecture. Thresholds Versus Fractional Expectation-Thresholds.
From www.slideshare.net
Distillation Thresholds Versus Fractional Expectation-Thresholds For an increasing family f on a finite set x, we write (with definitions below) pc(f), qf(f) and `(f) for the threshold, fractional expectation. Proving a conjecture of talagrand, a fractional version of the. For an increasing family ℱ {\mathcal {f}} on a finite set 𝑋 x, we write (with definitions below) subscript 𝑝 𝑐 ℱ p_ {c} ( {\mathcal. Thresholds Versus Fractional Expectation-Thresholds.
From www.researchgate.net
(PDF) Is it Time to Revisit Fractional Flow Reserve Thresholds? Thresholds Versus Fractional Expectation-Thresholds Proving a conjecture of talagrand, a fractional version of the. For an increasing family f on a finite set x, we write (with definitions below) pc(f), qf(f) and `(f) for the threshold, fractional expectation. $p_c \mathcal(f) = o(q_f (\mathcal{f}) \mathrm{log}\ell (\mathcal{f})$ for any increasing family $\mathcal{f}$ on a finite set $x$, where. For an increasing family ℱ {\mathcal {f}} on. Thresholds Versus Fractional Expectation-Thresholds.
From www.researchgate.net
Relative predictive power of functional and physical protein networks Thresholds Versus Fractional Expectation-Thresholds Proving a conjecture of talagrand, a fractional version of the. For an increasing family f on a finite set x, we write (with definitions below) pc(f), qf(f) and `(f) for the threshold, fractional expectation. $p_c \mathcal(f) = o(q_f (\mathcal{f}) \mathrm{log}\ell (\mathcal{f})$ for any increasing family $\mathcal{f}$ on a finite set $x$, where. For an increasing family ℱ {\mathcal {f}} on. Thresholds Versus Fractional Expectation-Thresholds.
From www.researchgate.net
Estimated thresholds versus tariff barriers. Download Scientific Diagram Thresholds Versus Fractional Expectation-Thresholds For an increasing family ℱ {\mathcal {f}} on a finite set 𝑋 x, we write (with definitions below) subscript 𝑝 𝑐 ℱ p_ {c} ( {\mathcal {f}}), subscript 𝑞 𝑓 ℱ q_ {f}. Proving a conjecture of talagrand, a fractional version of the. $p_c \mathcal(f) = o(q_f (\mathcal{f}) \mathrm{log}\ell (\mathcal{f})$ for any increasing family $\mathcal{f}$ on a finite set $x$,. Thresholds Versus Fractional Expectation-Thresholds.
From www.researchgate.net
FIGURE Hearing thresholds vs. hearing improvement. Hearing thresholds Thresholds Versus Fractional Expectation-Thresholds $p_c \mathcal(f) = o(q_f (\mathcal{f}) \mathrm{log}\ell (\mathcal{f})$ for any increasing family $\mathcal{f}$ on a finite set $x$, where. For an increasing family ℱ {\mathcal {f}} on a finite set 𝑋 x, we write (with definitions below) subscript 𝑝 𝑐 ℱ p_ {c} ( {\mathcal {f}}), subscript 𝑞 𝑓 ℱ q_ {f}. For an increasing family f on a finite set. Thresholds Versus Fractional Expectation-Thresholds.
From www.researchgate.net
5 Expectation value of the Mermin operator M as a function of Thresholds Versus Fractional Expectation-Thresholds For an increasing family ℱ {\mathcal {f}} on a finite set 𝑋 x, we write (with definitions below) subscript 𝑝 𝑐 ℱ p_ {c} ( {\mathcal {f}}), subscript 𝑞 𝑓 ℱ q_ {f}. $p_c \mathcal(f) = o(q_f (\mathcal{f}) \mathrm{log}\ell (\mathcal{f})$ for any increasing family $\mathcal{f}$ on a finite set $x$, where. For an increasing family f on a finite set. Thresholds Versus Fractional Expectation-Thresholds.
From www.ahajournals.org
A Simple, EvidenceBased Approach to Help Guide Diagnosis of Heart Thresholds Versus Fractional Expectation-Thresholds For an increasing family f on a finite set x, we write (with definitions below) pc(f), qf(f) and `(f) for the threshold, fractional expectation. Proving a conjecture of talagrand, a fractional version of the. For an increasing family ℱ {\mathcal {f}} on a finite set 𝑋 x, we write (with definitions below) subscript 𝑝 𝑐 ℱ p_ {c} ( {\mathcal. Thresholds Versus Fractional Expectation-Thresholds.