Filtering Random Process . Filtering, estimation, and detection clearly explains the basics of probability and random processes and details. Linear filtering of random processes. X (t − t0) to form y (t). In this chapter we study the problem of estimating the unobserved part using samples of the observed part. Q(z ) = 1 + q(1)z −1 + q(2)z −2 + · · ·. A process that can be factorized. (m, n) = h(m, n) ∗ x (m, n) where. The above example combines weighted values of x (t) and. In chapter 18 we also. Filtering, estimation, and detection clearly explains the basics of probability and random processes and details. The filter q(z ) is causal, stable, and minimum phase;
from dlsun.github.io
Filtering, estimation, and detection clearly explains the basics of probability and random processes and details. The filter q(z ) is causal, stable, and minimum phase; (m, n) = h(m, n) ∗ x (m, n) where. A process that can be factorized. Q(z ) = 1 + q(1)z −1 + q(2)z −2 + · · ·. Linear filtering of random processes. The above example combines weighted values of x (t) and. In this chapter we study the problem of estimating the unobserved part using samples of the observed part. Filtering, estimation, and detection clearly explains the basics of probability and random processes and details. X (t − t0) to form y (t).
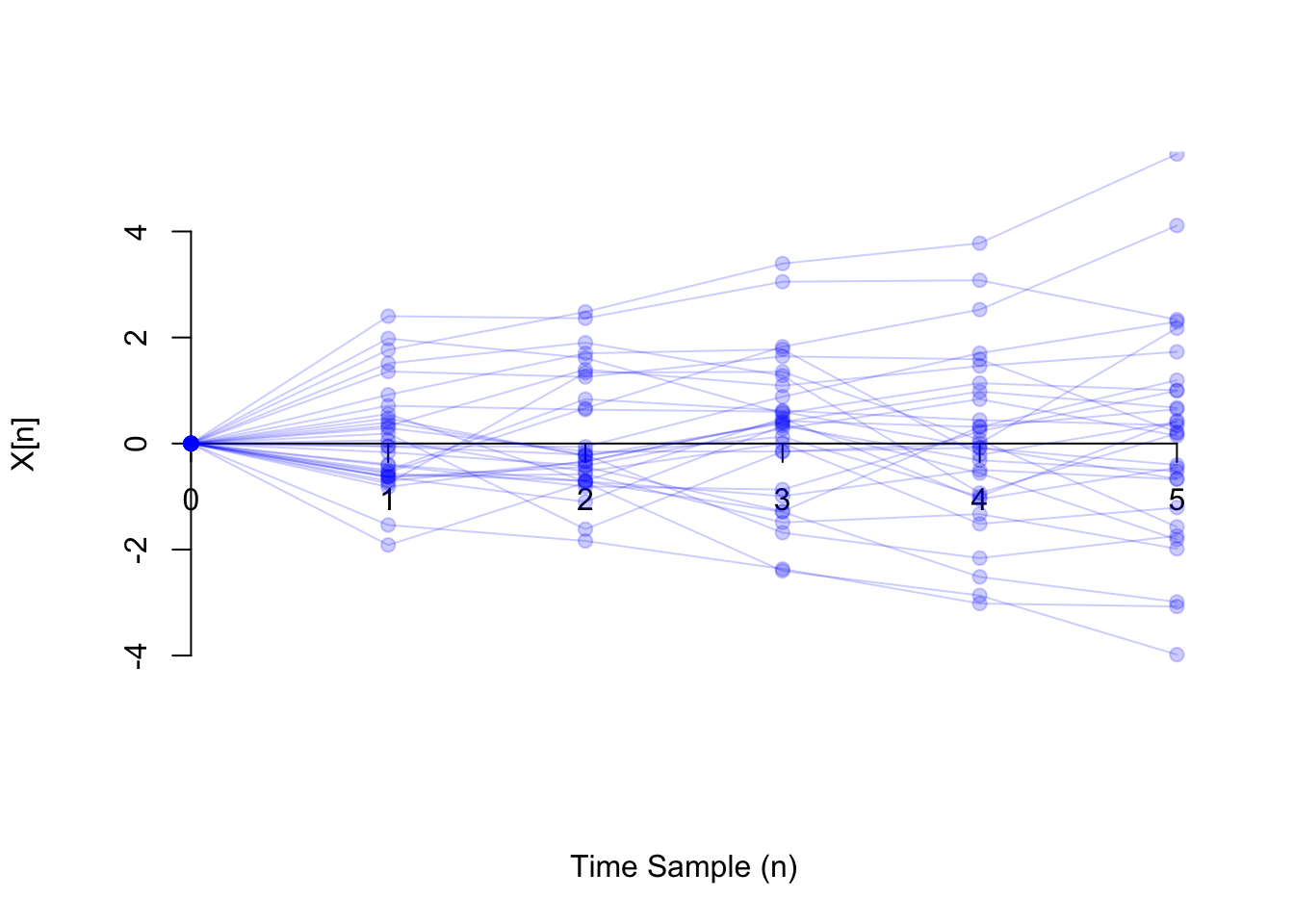
Lesson 47 Random Processes Introduction to Probability
Filtering Random Process Filtering, estimation, and detection clearly explains the basics of probability and random processes and details. Filtering, estimation, and detection clearly explains the basics of probability and random processes and details. Q(z ) = 1 + q(1)z −1 + q(2)z −2 + · · ·. X (t − t0) to form y (t). The filter q(z ) is causal, stable, and minimum phase; (m, n) = h(m, n) ∗ x (m, n) where. The above example combines weighted values of x (t) and. In this chapter we study the problem of estimating the unobserved part using samples of the observed part. Linear filtering of random processes. Filtering, estimation, and detection clearly explains the basics of probability and random processes and details. In chapter 18 we also. A process that can be factorized.
From www.researchgate.net
(PDF) Random Processes Filtering, Estimation, and Detection Filtering Random Process In this chapter we study the problem of estimating the unobserved part using samples of the observed part. In chapter 18 we also. X (t − t0) to form y (t). Filtering, estimation, and detection clearly explains the basics of probability and random processes and details. Linear filtering of random processes. The above example combines weighted values of x (t). Filtering Random Process.
From www.youtube.com
Transmission of random process through LTI filter YouTube Filtering Random Process Q(z ) = 1 + q(1)z −1 + q(2)z −2 + · · ·. The above example combines weighted values of x (t) and. The filter q(z ) is causal, stable, and minimum phase; X (t − t0) to form y (t). In this chapter we study the problem of estimating the unobserved part using samples of the observed part.. Filtering Random Process.
From dlsun.github.io
Lesson 48 Examples of Random Processes Introduction to Probability Filtering Random Process Filtering, estimation, and detection clearly explains the basics of probability and random processes and details. (m, n) = h(m, n) ∗ x (m, n) where. In chapter 18 we also. The above example combines weighted values of x (t) and. The filter q(z ) is causal, stable, and minimum phase; Filtering, estimation, and detection clearly explains the basics of probability. Filtering Random Process.
From www.researchgate.net
(PDF) Linear minimax filtering of scalar random process at presence of Filtering Random Process A process that can be factorized. Filtering, estimation, and detection clearly explains the basics of probability and random processes and details. The filter q(z ) is causal, stable, and minimum phase; In this chapter we study the problem of estimating the unobserved part using samples of the observed part. Q(z ) = 1 + q(1)z −1 + q(2)z −2 +. Filtering Random Process.
From www.youtube.com
Random Process (Part 1) YouTube Filtering Random Process (m, n) = h(m, n) ∗ x (m, n) where. The above example combines weighted values of x (t) and. In this chapter we study the problem of estimating the unobserved part using samples of the observed part. Linear filtering of random processes. Q(z ) = 1 + q(1)z −1 + q(2)z −2 + · · ·. A process that. Filtering Random Process.
From www.researchgate.net
(PDF) Filtering Random Graph Processes Over Random TimeVarying Graphs Filtering Random Process Linear filtering of random processes. In chapter 18 we also. (m, n) = h(m, n) ∗ x (m, n) where. A process that can be factorized. Filtering, estimation, and detection clearly explains the basics of probability and random processes and details. X (t − t0) to form y (t). Filtering, estimation, and detection clearly explains the basics of probability and. Filtering Random Process.
From www.researchgate.net
Realizations of Gaussian random fields with Gaussian covariance Filtering Random Process (m, n) = h(m, n) ∗ x (m, n) where. In chapter 18 we also. The filter q(z ) is causal, stable, and minimum phase; A process that can be factorized. In this chapter we study the problem of estimating the unobserved part using samples of the observed part. The above example combines weighted values of x (t) and. Linear. Filtering Random Process.
From www.youtube.com
Random Process Introduction With Example Difference between random Filtering Random Process The above example combines weighted values of x (t) and. Filtering, estimation, and detection clearly explains the basics of probability and random processes and details. X (t − t0) to form y (t). A process that can be factorized. The filter q(z ) is causal, stable, and minimum phase; Filtering, estimation, and detection clearly explains the basics of probability and. Filtering Random Process.
From www.numerade.com
SOLVED A widesense stationary random process X(t) has a power Filtering Random Process Filtering, estimation, and detection clearly explains the basics of probability and random processes and details. The filter q(z ) is causal, stable, and minimum phase; (m, n) = h(m, n) ∗ x (m, n) where. Linear filtering of random processes. X (t − t0) to form y (t). Q(z ) = 1 + q(1)z −1 + q(2)z −2 + ·. Filtering Random Process.
From www.oreilly.com
Title Page Random Processes Filtering, Estimation, and Detection [Book] Filtering Random Process The above example combines weighted values of x (t) and. X (t − t0) to form y (t). Q(z ) = 1 + q(1)z −1 + q(2)z −2 + · · ·. In this chapter we study the problem of estimating the unobserved part using samples of the observed part. A process that can be factorized. The filter q(z ). Filtering Random Process.
From www.youtube.com
HOW TO MAKE A RANDOM SELECTOR FILTER // 10 min tutorial with Spark AR Filtering Random Process In chapter 18 we also. Q(z ) = 1 + q(1)z −1 + q(2)z −2 + · · ·. In this chapter we study the problem of estimating the unobserved part using samples of the observed part. Linear filtering of random processes. The filter q(z ) is causal, stable, and minimum phase; X (t − t0) to form y (t).. Filtering Random Process.
From www.youtube.com
Filtering Random Process Discrete Time Random Processes Advanced Filtering Random Process Filtering, estimation, and detection clearly explains the basics of probability and random processes and details. The above example combines weighted values of x (t) and. In this chapter we study the problem of estimating the unobserved part using samples of the observed part. A process that can be factorized. Filtering, estimation, and detection clearly explains the basics of probability and. Filtering Random Process.
From studylib.net
WideSense Stationary Example Example (continued) Linear Filtering of Filtering Random Process Filtering, estimation, and detection clearly explains the basics of probability and random processes and details. (m, n) = h(m, n) ∗ x (m, n) where. Linear filtering of random processes. In this chapter we study the problem of estimating the unobserved part using samples of the observed part. The filter q(z ) is causal, stable, and minimum phase; The above. Filtering Random Process.
From www.jpc.de
Fourier Transforms, Filtering, Probability and Random Processes Jerry Filtering Random Process The above example combines weighted values of x (t) and. In chapter 18 we also. Filtering, estimation, and detection clearly explains the basics of probability and random processes and details. X (t − t0) to form y (t). Q(z ) = 1 + q(1)z −1 + q(2)z −2 + · · ·. In this chapter we study the problem of. Filtering Random Process.
From www.researchgate.net
(PDF) Maximum Cross Section Method in Optimal Filtering of Jump Filtering Random Process Linear filtering of random processes. Filtering, estimation, and detection clearly explains the basics of probability and random processes and details. Filtering, estimation, and detection clearly explains the basics of probability and random processes and details. Q(z ) = 1 + q(1)z −1 + q(2)z −2 + · · ·. The above example combines weighted values of x (t) and. In. Filtering Random Process.
From www.slideserve.com
PPT Chapter 5 Random Processes PowerPoint Presentation, free download Filtering Random Process Filtering, estimation, and detection clearly explains the basics of probability and random processes and details. The filter q(z ) is causal, stable, and minimum phase; (m, n) = h(m, n) ∗ x (m, n) where. A process that can be factorized. The above example combines weighted values of x (t) and. In this chapter we study the problem of estimating. Filtering Random Process.
From www.chegg.com
Solved 1) Random Processes Suppose that a widesense Filtering Random Process Linear filtering of random processes. The above example combines weighted values of x (t) and. Filtering, estimation, and detection clearly explains the basics of probability and random processes and details. The filter q(z ) is causal, stable, and minimum phase; A process that can be factorized. In this chapter we study the problem of estimating the unobserved part using samples. Filtering Random Process.
From www.slideserve.com
PPT Random processes basic concepts PowerPoint Presentation, free Filtering Random Process Filtering, estimation, and detection clearly explains the basics of probability and random processes and details. Linear filtering of random processes. In chapter 18 we also. Q(z ) = 1 + q(1)z −1 + q(2)z −2 + · · ·. Filtering, estimation, and detection clearly explains the basics of probability and random processes and details. A process that can be factorized.. Filtering Random Process.
From www.researchgate.net
(PDF) Maximum Cross Section Method in Optimal Filtering of Jump Filtering Random Process X (t − t0) to form y (t). In chapter 18 we also. Filtering, estimation, and detection clearly explains the basics of probability and random processes and details. A process that can be factorized. Linear filtering of random processes. Filtering, estimation, and detection clearly explains the basics of probability and random processes and details. The above example combines weighted values. Filtering Random Process.
From www.youtube.com
Transmission of Random Process through LTI Filter YouTube Filtering Random Process The above example combines weighted values of x (t) and. In this chapter we study the problem of estimating the unobserved part using samples of the observed part. The filter q(z ) is causal, stable, and minimum phase; Filtering, estimation, and detection clearly explains the basics of probability and random processes and details. Q(z ) = 1 + q(1)z −1. Filtering Random Process.
From www.slideserve.com
PPT Chapter 1 Random Process PowerPoint Presentation, free download Filtering Random Process The above example combines weighted values of x (t) and. Filtering, estimation, and detection clearly explains the basics of probability and random processes and details. In this chapter we study the problem of estimating the unobserved part using samples of the observed part. In chapter 18 we also. The filter q(z ) is causal, stable, and minimum phase; Linear filtering. Filtering Random Process.
From dlsun.github.io
Lesson 47 Random Processes Introduction to Probability Filtering Random Process The filter q(z ) is causal, stable, and minimum phase; A process that can be factorized. The above example combines weighted values of x (t) and. In this chapter we study the problem of estimating the unobserved part using samples of the observed part. (m, n) = h(m, n) ∗ x (m, n) where. Filtering, estimation, and detection clearly explains. Filtering Random Process.
From www.researchgate.net
(PDF) Robust adaptive filtering algorithms for ??stable random processes Filtering Random Process In chapter 18 we also. The above example combines weighted values of x (t) and. Linear filtering of random processes. Filtering, estimation, and detection clearly explains the basics of probability and random processes and details. The filter q(z ) is causal, stable, and minimum phase; (m, n) = h(m, n) ∗ x (m, n) where. In this chapter we study. Filtering Random Process.
From dlsun.github.io
Lesson 47 Random Processes Introduction to Probability Filtering Random Process X (t − t0) to form y (t). In chapter 18 we also. In this chapter we study the problem of estimating the unobserved part using samples of the observed part. The filter q(z ) is causal, stable, and minimum phase; Filtering, estimation, and detection clearly explains the basics of probability and random processes and details. (m, n) = h(m,. Filtering Random Process.
From www.oreilly.com
APPENDIX E Table for Gaussian Cumulative Distribution Function Filtering Random Process Filtering, estimation, and detection clearly explains the basics of probability and random processes and details. A process that can be factorized. Filtering, estimation, and detection clearly explains the basics of probability and random processes and details. The filter q(z ) is causal, stable, and minimum phase; In this chapter we study the problem of estimating the unobserved part using samples. Filtering Random Process.
From www.youtube.com
2022 Adding and Filtering Random Noise (Median Filter) from an Image in Filtering Random Process The above example combines weighted values of x (t) and. Filtering, estimation, and detection clearly explains the basics of probability and random processes and details. In chapter 18 we also. A process that can be factorized. Filtering, estimation, and detection clearly explains the basics of probability and random processes and details. The filter q(z ) is causal, stable, and minimum. Filtering Random Process.
From www.researchgate.net
(PDF) Filtering Problem for Random Processes with Stationary Increments Filtering Random Process The above example combines weighted values of x (t) and. X (t − t0) to form y (t). (m, n) = h(m, n) ∗ x (m, n) where. The filter q(z ) is causal, stable, and minimum phase; In this chapter we study the problem of estimating the unobserved part using samples of the observed part. A process that can. Filtering Random Process.
From www.slideserve.com
PPT Chapter 6 Random Processes PowerPoint Presentation, free download Filtering Random Process In chapter 18 we also. In this chapter we study the problem of estimating the unobserved part using samples of the observed part. Filtering, estimation, and detection clearly explains the basics of probability and random processes and details. Q(z ) = 1 + q(1)z −1 + q(2)z −2 + · · ·. (m, n) = h(m, n) ∗ x (m,. Filtering Random Process.
From www.researchgate.net
The process of filtering generated samples. Download Scientific Diagram Filtering Random Process The above example combines weighted values of x (t) and. Filtering, estimation, and detection clearly explains the basics of probability and random processes and details. Linear filtering of random processes. (m, n) = h(m, n) ∗ x (m, n) where. X (t − t0) to form y (t). Filtering, estimation, and detection clearly explains the basics of probability and random. Filtering Random Process.
From www.scribd.com
ELEC5300 Lecture 4 Continuous Time Linear Systems A Review Filtering Filtering Random Process In this chapter we study the problem of estimating the unobserved part using samples of the observed part. Q(z ) = 1 + q(1)z −1 + q(2)z −2 + · · ·. Filtering, estimation, and detection clearly explains the basics of probability and random processes and details. X (t − t0) to form y (t). The filter q(z ) is. Filtering Random Process.
From www.slideserve.com
PPT Basic Random Processes PowerPoint Presentation, free download Filtering Random Process Q(z ) = 1 + q(1)z −1 + q(2)z −2 + · · ·. (m, n) = h(m, n) ∗ x (m, n) where. X (t − t0) to form y (t). Filtering, estimation, and detection clearly explains the basics of probability and random processes and details. The above example combines weighted values of x (t) and. A process that. Filtering Random Process.
From www.researchgate.net
Signals from two shot noise random processes, as defined by Equation Filtering Random Process (m, n) = h(m, n) ∗ x (m, n) where. X (t − t0) to form y (t). Filtering, estimation, and detection clearly explains the basics of probability and random processes and details. In chapter 18 we also. A process that can be factorized. In this chapter we study the problem of estimating the unobserved part using samples of the. Filtering Random Process.
From dlsun.github.io
Lesson 48 Examples of Random Processes Introduction to Probability Filtering Random Process The above example combines weighted values of x (t) and. In this chapter we study the problem of estimating the unobserved part using samples of the observed part. Linear filtering of random processes. X (t − t0) to form y (t). Filtering, estimation, and detection clearly explains the basics of probability and random processes and details. A process that can. Filtering Random Process.
From www.slideserve.com
PPT Basic Random Processes PowerPoint Presentation, free download Filtering Random Process In chapter 18 we also. X (t − t0) to form y (t). Linear filtering of random processes. (m, n) = h(m, n) ∗ x (m, n) where. A process that can be factorized. Q(z ) = 1 + q(1)z −1 + q(2)z −2 + · · ·. Filtering, estimation, and detection clearly explains the basics of probability and random. Filtering Random Process.
From www.slideserve.com
PPT Chapter 5 Random Processes PowerPoint Presentation, free download Filtering Random Process The above example combines weighted values of x (t) and. Q(z ) = 1 + q(1)z −1 + q(2)z −2 + · · ·. In chapter 18 we also. In this chapter we study the problem of estimating the unobserved part using samples of the observed part. Filtering, estimation, and detection clearly explains the basics of probability and random processes. Filtering Random Process.