Is Zero Vector A Subspace . Any subspace of a vector space \(v\) which is not equal to \(v\) or \(\left\{ \vec{0} \right\}\) is called a proper subspace. The subspace containing only the zero vector vacuously satisfies all the properties required of a subspace. Yes the set containing only the zero vector is a subspace of $\bbb r^n$. Indeed, it contains zero, and is closed under addition and scalar multiplication. Determine if a set of vectors is. It can arise in many ways by operations that always produce. A subspace of \\(\\mathbb{r}^n\\) is a subset that contains the zero vector and is closed under addition and scalar multiplication. Learn how to recognize and construct. There is one vector in this subspace (namely, the zero vector), so shouldn't the dimension be 1? Is there an intuitive way to. Determine the span of a set of vectors, and determine if a vector is contained in a specified span. The set r n is a subspace of itself:
from www.chegg.com
Yes the set containing only the zero vector is a subspace of $\bbb r^n$. Learn how to recognize and construct. Any subspace of a vector space \(v\) which is not equal to \(v\) or \(\left\{ \vec{0} \right\}\) is called a proper subspace. Indeed, it contains zero, and is closed under addition and scalar multiplication. A subspace of \\(\\mathbb{r}^n\\) is a subset that contains the zero vector and is closed under addition and scalar multiplication. Determine if a set of vectors is. The set r n is a subspace of itself: Is there an intuitive way to. The subspace containing only the zero vector vacuously satisfies all the properties required of a subspace. There is one vector in this subspace (namely, the zero vector), so shouldn't the dimension be 1?
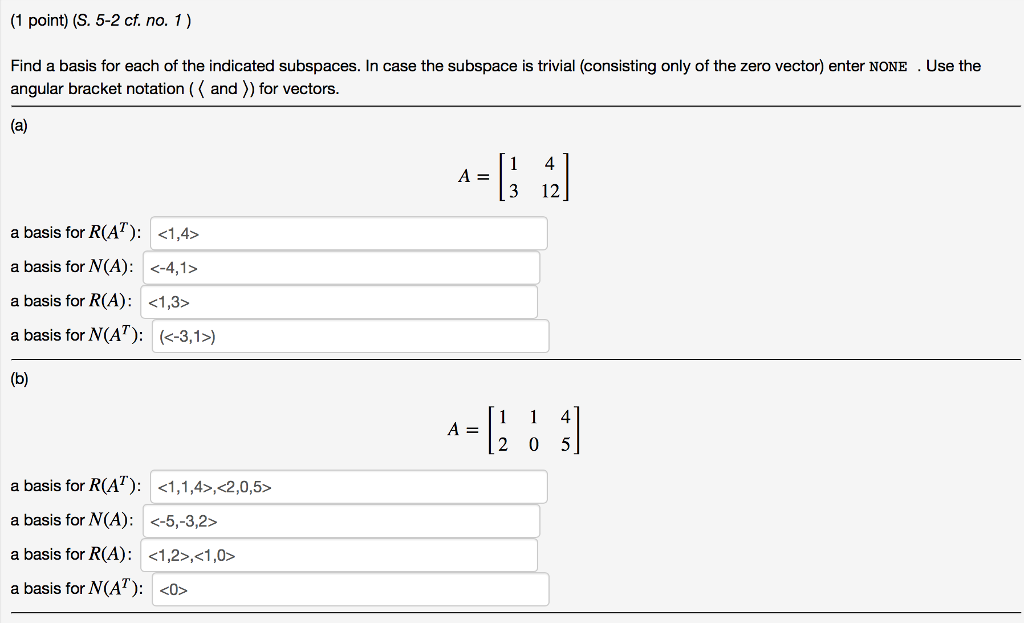
Solved Find a basis for each of the indicated subspaces In
Is Zero Vector A Subspace Any subspace of a vector space \(v\) which is not equal to \(v\) or \(\left\{ \vec{0} \right\}\) is called a proper subspace. The subspace containing only the zero vector vacuously satisfies all the properties required of a subspace. There is one vector in this subspace (namely, the zero vector), so shouldn't the dimension be 1? Is there an intuitive way to. Determine the span of a set of vectors, and determine if a vector is contained in a specified span. Yes the set containing only the zero vector is a subspace of $\bbb r^n$. It can arise in many ways by operations that always produce. Indeed, it contains zero, and is closed under addition and scalar multiplication. Learn how to recognize and construct. Determine if a set of vectors is. The set r n is a subspace of itself: Any subspace of a vector space \(v\) which is not equal to \(v\) or \(\left\{ \vec{0} \right\}\) is called a proper subspace. A subspace of \\(\\mathbb{r}^n\\) is a subset that contains the zero vector and is closed under addition and scalar multiplication.
From www.slideserve.com
PPT Chapter 3 Vector Space PowerPoint Presentation, free download ID5593854 Is Zero Vector A Subspace Indeed, it contains zero, and is closed under addition and scalar multiplication. The set r n is a subspace of itself: It can arise in many ways by operations that always produce. Determine the span of a set of vectors, and determine if a vector is contained in a specified span. Is there an intuitive way to. Any subspace of. Is Zero Vector A Subspace.
From slideplayer.com
VECTOR SPACES AND SUBSPACES ppt download Is Zero Vector A Subspace Determine if a set of vectors is. Determine the span of a set of vectors, and determine if a vector is contained in a specified span. Is there an intuitive way to. Learn how to recognize and construct. The subspace containing only the zero vector vacuously satisfies all the properties required of a subspace. It can arise in many ways. Is Zero Vector A Subspace.
From www.numerade.com
Prove that W = (x,y,z) ∈R3 x + 2y + 3z = 0 is a vector subspace of R3 by using the Subspace Test. Is Zero Vector A Subspace Determine the span of a set of vectors, and determine if a vector is contained in a specified span. Learn how to recognize and construct. Determine if a set of vectors is. A subspace of \\(\\mathbb{r}^n\\) is a subset that contains the zero vector and is closed under addition and scalar multiplication. Any subspace of a vector space \(v\) which. Is Zero Vector A Subspace.
From www.numerade.com
SOLVED Every vector space W contains at least one subspace which is the zero subspace. Select Is Zero Vector A Subspace Is there an intuitive way to. Indeed, it contains zero, and is closed under addition and scalar multiplication. It can arise in many ways by operations that always produce. There is one vector in this subspace (namely, the zero vector), so shouldn't the dimension be 1? A subspace of \\(\\mathbb{r}^n\\) is a subset that contains the zero vector and is. Is Zero Vector A Subspace.
From vectorified.com
What Is A Zero Vector at Collection of What Is A Zero Vector free for personal use Is Zero Vector A Subspace There is one vector in this subspace (namely, the zero vector), so shouldn't the dimension be 1? Determine the span of a set of vectors, and determine if a vector is contained in a specified span. Determine if a set of vectors is. Learn how to recognize and construct. Any subspace of a vector space \(v\) which is not equal. Is Zero Vector A Subspace.
From www.researchgate.net
Diagram showing subspaces of wave vector superposition (a) subspaces... Download Scientific Is Zero Vector A Subspace Any subspace of a vector space \(v\) which is not equal to \(v\) or \(\left\{ \vec{0} \right\}\) is called a proper subspace. The subspace containing only the zero vector vacuously satisfies all the properties required of a subspace. Determine if a set of vectors is. Is there an intuitive way to. Learn how to recognize and construct. It can arise. Is Zero Vector A Subspace.
From slideplayer.com
VECTOR SPACES AND SUBSPACES ppt download Is Zero Vector A Subspace Determine if a set of vectors is. Indeed, it contains zero, and is closed under addition and scalar multiplication. There is one vector in this subspace (namely, the zero vector), so shouldn't the dimension be 1? Determine the span of a set of vectors, and determine if a vector is contained in a specified span. The subspace containing only the. Is Zero Vector A Subspace.
From www.slideserve.com
PPT Chapter 4 ( B ) PowerPoint Presentation, free download ID6075045 Is Zero Vector A Subspace There is one vector in this subspace (namely, the zero vector), so shouldn't the dimension be 1? Yes the set containing only the zero vector is a subspace of $\bbb r^n$. The set r n is a subspace of itself: Any subspace of a vector space \(v\) which is not equal to \(v\) or \(\left\{ \vec{0} \right\}\) is called a. Is Zero Vector A Subspace.
From ar.inspiredpencil.com
Vector Spaces And Subspaces Is Zero Vector A Subspace Any subspace of a vector space \(v\) which is not equal to \(v\) or \(\left\{ \vec{0} \right\}\) is called a proper subspace. Yes the set containing only the zero vector is a subspace of $\bbb r^n$. A subspace of \\(\\mathbb{r}^n\\) is a subset that contains the zero vector and is closed under addition and scalar multiplication. Determine the span of. Is Zero Vector A Subspace.
From www.numerade.com
SOLVED Determine if the subset of R consisting of vectors of the form where a > 0, b > 0,and c Is Zero Vector A Subspace The set r n is a subspace of itself: Determine the span of a set of vectors, and determine if a vector is contained in a specified span. A subspace of \\(\\mathbb{r}^n\\) is a subset that contains the zero vector and is closed under addition and scalar multiplication. Determine if a set of vectors is. Is there an intuitive way. Is Zero Vector A Subspace.
From eevibes.com
what is the vector space in linear algebra? vector space example EEVibes Is Zero Vector A Subspace Indeed, it contains zero, and is closed under addition and scalar multiplication. Determine if a set of vectors is. Yes the set containing only the zero vector is a subspace of $\bbb r^n$. Learn how to recognize and construct. A subspace of \\(\\mathbb{r}^n\\) is a subset that contains the zero vector and is closed under addition and scalar multiplication. Determine. Is Zero Vector A Subspace.
From www.chegg.com
Solved All vectors and subspaces are in R”. Note you only Is Zero Vector A Subspace Is there an intuitive way to. Learn how to recognize and construct. The subspace containing only the zero vector vacuously satisfies all the properties required of a subspace. The set r n is a subspace of itself: Any subspace of a vector space \(v\) which is not equal to \(v\) or \(\left\{ \vec{0} \right\}\) is called a proper subspace. It. Is Zero Vector A Subspace.
From www.youtube.com
Zero vector of space M (2 *2 Matrices) and Matrices in smallest Subspace containing A Pr 314 Is Zero Vector A Subspace Determine the span of a set of vectors, and determine if a vector is contained in a specified span. Is there an intuitive way to. Determine if a set of vectors is. The subspace containing only the zero vector vacuously satisfies all the properties required of a subspace. A subspace of \\(\\mathbb{r}^n\\) is a subset that contains the zero vector. Is Zero Vector A Subspace.
From www.chegg.com
Solved Find a basis for each of the indicated subspaces In Is Zero Vector A Subspace Any subspace of a vector space \(v\) which is not equal to \(v\) or \(\left\{ \vec{0} \right\}\) is called a proper subspace. It can arise in many ways by operations that always produce. Learn how to recognize and construct. Yes the set containing only the zero vector is a subspace of $\bbb r^n$. There is one vector in this subspace. Is Zero Vector A Subspace.
From vectorified.com
What Is A Zero Vector at Collection of What Is A Zero Vector free for personal use Is Zero Vector A Subspace Yes the set containing only the zero vector is a subspace of $\bbb r^n$. The set r n is a subspace of itself: Is there an intuitive way to. It can arise in many ways by operations that always produce. Learn how to recognize and construct. Determine if a set of vectors is. Indeed, it contains zero, and is closed. Is Zero Vector A Subspace.
From www.numerade.com
SOLVEDRedraw Figure 3.4 for a 3 by 2 matrix of rank r=2. Which subspace is Z (zero vector only Is Zero Vector A Subspace A subspace of \\(\\mathbb{r}^n\\) is a subset that contains the zero vector and is closed under addition and scalar multiplication. Determine if a set of vectors is. Yes the set containing only the zero vector is a subspace of $\bbb r^n$. Determine the span of a set of vectors, and determine if a vector is contained in a specified span.. Is Zero Vector A Subspace.
From www.youtube.com
Linear Algebra Example Problems Subspace Example 1 YouTube Is Zero Vector A Subspace A subspace of \\(\\mathbb{r}^n\\) is a subset that contains the zero vector and is closed under addition and scalar multiplication. Learn how to recognize and construct. Any subspace of a vector space \(v\) which is not equal to \(v\) or \(\left\{ \vec{0} \right\}\) is called a proper subspace. Is there an intuitive way to. Yes the set containing only the. Is Zero Vector A Subspace.
From vectorified.com
Zero Vector at Collection of Zero Vector free for personal use Is Zero Vector A Subspace Is there an intuitive way to. It can arise in many ways by operations that always produce. A subspace of \\(\\mathbb{r}^n\\) is a subset that contains the zero vector and is closed under addition and scalar multiplication. Any subspace of a vector space \(v\) which is not equal to \(v\) or \(\left\{ \vec{0} \right\}\) is called a proper subspace. Determine. Is Zero Vector A Subspace.
From slideplayer.com
VECTOR SPACES AND SUBSPACES ppt download Is Zero Vector A Subspace Is there an intuitive way to. It can arise in many ways by operations that always produce. Indeed, it contains zero, and is closed under addition and scalar multiplication. Learn how to recognize and construct. There is one vector in this subspace (namely, the zero vector), so shouldn't the dimension be 1? Determine if a set of vectors is. Any. Is Zero Vector A Subspace.
From slideplayer.com
ABASAHEB KAKADE ARTS COLLEGE BODHEGAON ppt download Is Zero Vector A Subspace Is there an intuitive way to. Any subspace of a vector space \(v\) which is not equal to \(v\) or \(\left\{ \vec{0} \right\}\) is called a proper subspace. A subspace of \\(\\mathbb{r}^n\\) is a subset that contains the zero vector and is closed under addition and scalar multiplication. There is one vector in this subspace (namely, the zero vector), so. Is Zero Vector A Subspace.
From porttiklo.weebly.com
Subspace definition vector porttiklo Is Zero Vector A Subspace Any subspace of a vector space \(v\) which is not equal to \(v\) or \(\left\{ \vec{0} \right\}\) is called a proper subspace. Determine the span of a set of vectors, and determine if a vector is contained in a specified span. A subspace of \\(\\mathbb{r}^n\\) is a subset that contains the zero vector and is closed under addition and scalar. Is Zero Vector A Subspace.
From mungfali.com
What Is A Subspace Is Zero Vector A Subspace Any subspace of a vector space \(v\) which is not equal to \(v\) or \(\left\{ \vec{0} \right\}\) is called a proper subspace. Is there an intuitive way to. Determine if a set of vectors is. Learn how to recognize and construct. A subspace of \\(\\mathbb{r}^n\\) is a subset that contains the zero vector and is closed under addition and scalar. Is Zero Vector A Subspace.
From slideplayer.com
Engineering Analysis Chapter 3 Vector Spaces. ppt download Is Zero Vector A Subspace Indeed, it contains zero, and is closed under addition and scalar multiplication. Any subspace of a vector space \(v\) which is not equal to \(v\) or \(\left\{ \vec{0} \right\}\) is called a proper subspace. Learn how to recognize and construct. Determine if a set of vectors is. A subspace of \\(\\mathbb{r}^n\\) is a subset that contains the zero vector and. Is Zero Vector A Subspace.
From www.numerade.com
If 𝐕 and 𝐖 are orthogonal subspaces, show that the only vector they have in common is the zero Is Zero Vector A Subspace The subspace containing only the zero vector vacuously satisfies all the properties required of a subspace. Yes the set containing only the zero vector is a subspace of $\bbb r^n$. Is there an intuitive way to. Any subspace of a vector space \(v\) which is not equal to \(v\) or \(\left\{ \vec{0} \right\}\) is called a proper subspace. The set. Is Zero Vector A Subspace.
From www.slideserve.com
PPT Chapter 3 Vector Spaces PowerPoint Presentation, free download ID5738812 Is Zero Vector A Subspace Any subspace of a vector space \(v\) which is not equal to \(v\) or \(\left\{ \vec{0} \right\}\) is called a proper subspace. There is one vector in this subspace (namely, the zero vector), so shouldn't the dimension be 1? Determine if a set of vectors is. Is there an intuitive way to. Learn how to recognize and construct. A subspace. Is Zero Vector A Subspace.
From www.slideserve.com
PPT Chapter 3 Vector Space PowerPoint Presentation, free download ID5593854 Is Zero Vector A Subspace It can arise in many ways by operations that always produce. The set r n is a subspace of itself: Determine if a set of vectors is. Indeed, it contains zero, and is closed under addition and scalar multiplication. Determine the span of a set of vectors, and determine if a vector is contained in a specified span. Is there. Is Zero Vector A Subspace.
From www.youtube.com
subspaces of r cube r3 vector space scalar multiplication iit jam 2014 linear algebra Is Zero Vector A Subspace Learn how to recognize and construct. It can arise in many ways by operations that always produce. Yes the set containing only the zero vector is a subspace of $\bbb r^n$. Determine if a set of vectors is. Any subspace of a vector space \(v\) which is not equal to \(v\) or \(\left\{ \vec{0} \right\}\) is called a proper subspace.. Is Zero Vector A Subspace.
From www.kristakingmath.com
A span is always a subspace — Krista King Math Online math help Is Zero Vector A Subspace Indeed, it contains zero, and is closed under addition and scalar multiplication. Yes the set containing only the zero vector is a subspace of $\bbb r^n$. Any subspace of a vector space \(v\) which is not equal to \(v\) or \(\left\{ \vec{0} \right\}\) is called a proper subspace. There is one vector in this subspace (namely, the zero vector), so. Is Zero Vector A Subspace.
From www.youtube.com
Lecture 7 Vector Spaces and Subspaces, the Column Space and the Nullspace YouTube Is Zero Vector A Subspace It can arise in many ways by operations that always produce. Is there an intuitive way to. There is one vector in this subspace (namely, the zero vector), so shouldn't the dimension be 1? Any subspace of a vector space \(v\) which is not equal to \(v\) or \(\left\{ \vec{0} \right\}\) is called a proper subspace. Learn how to recognize. Is Zero Vector A Subspace.
From www.numerade.com
SOLVED Determine if the subset of R? consisting of vectors of the form where a 2 0, b > 0,and c Is Zero Vector A Subspace The subspace containing only the zero vector vacuously satisfies all the properties required of a subspace. Is there an intuitive way to. Yes the set containing only the zero vector is a subspace of $\bbb r^n$. The set r n is a subspace of itself: Any subspace of a vector space \(v\) which is not equal to \(v\) or \(\left\{. Is Zero Vector A Subspace.
From www.youtube.com
What is a Vector Subspace? An example of a not vector subspace. YouTube Is Zero Vector A Subspace Determine if a set of vectors is. The subspace containing only the zero vector vacuously satisfies all the properties required of a subspace. Determine the span of a set of vectors, and determine if a vector is contained in a specified span. Is there an intuitive way to. Yes the set containing only the zero vector is a subspace of. Is Zero Vector A Subspace.
From www.reddit.com
[Linear Algebra] Why is 3) a subspace of R3? Following the equation, the only vector in the set Is Zero Vector A Subspace Indeed, it contains zero, and is closed under addition and scalar multiplication. It can arise in many ways by operations that always produce. Is there an intuitive way to. A subspace of \\(\\mathbb{r}^n\\) is a subset that contains the zero vector and is closed under addition and scalar multiplication. The subspace containing only the zero vector vacuously satisfies all the. Is Zero Vector A Subspace.
From www.youtube.com
Determine if W = {(a, b, c) b ≥ 0} is a Subspace of the Vector Space R^3 YouTube Is Zero Vector A Subspace It can arise in many ways by operations that always produce. The subspace containing only the zero vector vacuously satisfies all the properties required of a subspace. There is one vector in this subspace (namely, the zero vector), so shouldn't the dimension be 1? Learn how to recognize and construct. Is there an intuitive way to. Indeed, it contains zero,. Is Zero Vector A Subspace.
From www.chegg.com
Solved For each of the following subsets of the vector space Is Zero Vector A Subspace Learn how to recognize and construct. Indeed, it contains zero, and is closed under addition and scalar multiplication. It can arise in many ways by operations that always produce. The set r n is a subspace of itself: Determine the span of a set of vectors, and determine if a vector is contained in a specified span. There is one. Is Zero Vector A Subspace.
From slideplayer.com
VECTOR SPACES AND SUBSPACES ppt download Is Zero Vector A Subspace There is one vector in this subspace (namely, the zero vector), so shouldn't the dimension be 1? Yes the set containing only the zero vector is a subspace of $\bbb r^n$. Any subspace of a vector space \(v\) which is not equal to \(v\) or \(\left\{ \vec{0} \right\}\) is called a proper subspace. A subspace of \\(\\mathbb{r}^n\\) is a subset. Is Zero Vector A Subspace.