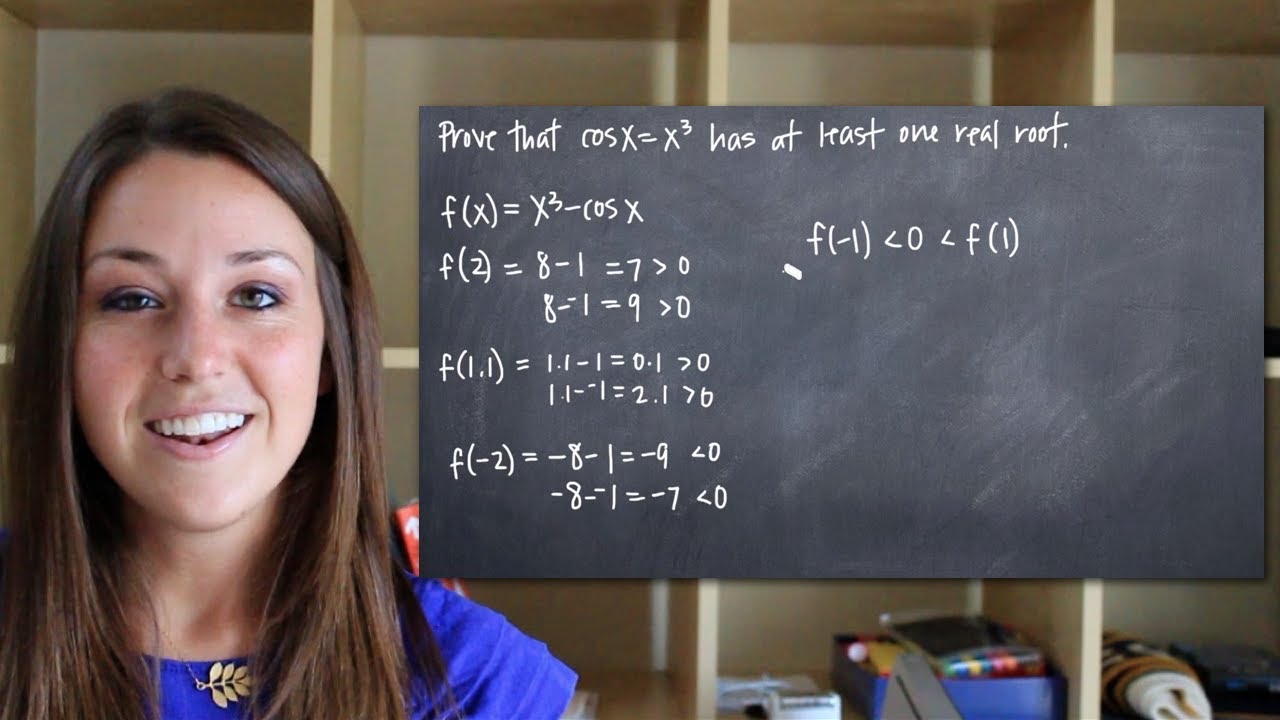How To Prove Real Roots . whether the discriminant is greater than zero, equal to zero or less than zero can be used to determine if a quadratic equation has no real roots, real and equal. follow these general steps to ensure that you find every root: find the real roots of each equation by factoring or using the quadratic formula. Use the rational root theorem to list all possible rational roots. a) show that a polynomial of degree 3 has at most three real roots. In the special case that f is a. B) show that a polynomial of degree n has at most n real. to prove existence of roots of a continuous function, you can exhibit changes of sign. here’s how descartes’s rule of signs can give you the numbers of possible real roots, both positive and negative: in your example, computing f(±2) = 3 and f(0) = −1 gives that f has one root each in (−2, 0) and (0, +2).
from www.youtube.com
B) show that a polynomial of degree n has at most n real. whether the discriminant is greater than zero, equal to zero or less than zero can be used to determine if a quadratic equation has no real roots, real and equal. follow these general steps to ensure that you find every root: Use the rational root theorem to list all possible rational roots. In the special case that f is a. a) show that a polynomial of degree 3 has at most three real roots. to prove existence of roots of a continuous function, you can exhibit changes of sign. in your example, computing f(±2) = 3 and f(0) = −1 gives that f has one root each in (−2, 0) and (0, +2). here’s how descartes’s rule of signs can give you the numbers of possible real roots, both positive and negative: find the real roots of each equation by factoring or using the quadratic formula.
Prove the equation has at least one real root (KristaKingMath) YouTube
How To Prove Real Roots Use the rational root theorem to list all possible rational roots. Use the rational root theorem to list all possible rational roots. In the special case that f is a. in your example, computing f(±2) = 3 and f(0) = −1 gives that f has one root each in (−2, 0) and (0, +2). here’s how descartes’s rule of signs can give you the numbers of possible real roots, both positive and negative: whether the discriminant is greater than zero, equal to zero or less than zero can be used to determine if a quadratic equation has no real roots, real and equal. follow these general steps to ensure that you find every root: B) show that a polynomial of degree n has at most n real. a) show that a polynomial of degree 3 has at most three real roots. find the real roots of each equation by factoring or using the quadratic formula. to prove existence of roots of a continuous function, you can exhibit changes of sign.
From www.youtube.com
Can You Determine if a Quadratic Equation has Real Roots? If so, Find the Roots Simple How To Prove Real Roots follow these general steps to ensure that you find every root: whether the discriminant is greater than zero, equal to zero or less than zero can be used to determine if a quadratic equation has no real roots, real and equal. to prove existence of roots of a continuous function, you can exhibit changes of sign. B). How To Prove Real Roots.
From lessonschoollineages.z13.web.core.windows.net
Sum And Product Of The Roots Calculator How To Prove Real Roots whether the discriminant is greater than zero, equal to zero or less than zero can be used to determine if a quadratic equation has no real roots, real and equal. Use the rational root theorem to list all possible rational roots. In the special case that f is a. to prove existence of roots of a continuous function,. How To Prove Real Roots.
From www.youtube.com
Quadratic Equations Nature of Roots Real and Equal Roots YouTube How To Prove Real Roots B) show that a polynomial of degree n has at most n real. Use the rational root theorem to list all possible rational roots. follow these general steps to ensure that you find every root: a) show that a polynomial of degree 3 has at most three real roots. in your example, computing f(±2) = 3 and. How To Prove Real Roots.
From www.ck12.org
Finding Real nth Roots of a (n is an integer) Overview ( Video ) Algebra CK12 Foundation How To Prove Real Roots to prove existence of roots of a continuous function, you can exhibit changes of sign. Use the rational root theorem to list all possible rational roots. a) show that a polynomial of degree 3 has at most three real roots. in your example, computing f(±2) = 3 and f(0) = −1 gives that f has one root. How To Prove Real Roots.
From www.youtube.com
Equations Part 24 Prove Roots are Real Exercise 3.5 Q3 11 Class P34 YouTube How To Prove Real Roots a) show that a polynomial of degree 3 has at most three real roots. find the real roots of each equation by factoring or using the quadratic formula. in your example, computing f(±2) = 3 and f(0) = −1 gives that f has one root each in (−2, 0) and (0, +2). here’s how descartes’s rule. How To Prove Real Roots.
From slidetodoc.com
Finding Real Roots of Polynomial Equations How do How To Prove Real Roots B) show that a polynomial of degree n has at most n real. in your example, computing f(±2) = 3 and f(0) = −1 gives that f has one root each in (−2, 0) and (0, +2). a) show that a polynomial of degree 3 has at most three real roots. Use the rational root theorem to list. How To Prove Real Roots.
From www.slideserve.com
PPT Fundamental Theorem of Algebra and Finding Real Roots PowerPoint Presentation ID2666595 How To Prove Real Roots in your example, computing f(±2) = 3 and f(0) = −1 gives that f has one root each in (−2, 0) and (0, +2). B) show that a polynomial of degree n has at most n real. find the real roots of each equation by factoring or using the quadratic formula. Use the rational root theorem to list. How To Prove Real Roots.
From www.teachoo.com
Prove that root 2 is irrational Teachoo [with Video] Examples How To Prove Real Roots in your example, computing f(±2) = 3 and f(0) = −1 gives that f has one root each in (−2, 0) and (0, +2). here’s how descartes’s rule of signs can give you the numbers of possible real roots, both positive and negative: B) show that a polynomial of degree n has at most n real. follow. How To Prove Real Roots.
From www.chegg.com
Solved 012 10.0 points How many real roots does the equation How To Prove Real Roots a) show that a polynomial of degree 3 has at most three real roots. Use the rational root theorem to list all possible rational roots. whether the discriminant is greater than zero, equal to zero or less than zero can be used to determine if a quadratic equation has no real roots, real and equal. follow these. How To Prove Real Roots.
From www.youtube.com
Conjugate Root Theorems Real Roots Algebra 2 YouTube How To Prove Real Roots whether the discriminant is greater than zero, equal to zero or less than zero can be used to determine if a quadratic equation has no real roots, real and equal. to prove existence of roots of a continuous function, you can exhibit changes of sign. B) show that a polynomial of degree n has at most n real.. How To Prove Real Roots.
From www.youtube.com
Show that the equation `2x^(2)6x+3=0` has real roots and find these roots. YouTube How To Prove Real Roots In the special case that f is a. to prove existence of roots of a continuous function, you can exhibit changes of sign. find the real roots of each equation by factoring or using the quadratic formula. Use the rational root theorem to list all possible rational roots. a) show that a polynomial of degree 3 has. How To Prove Real Roots.
From www.youtube.com
Possible roots of a Polynomial Equation YouTube How To Prove Real Roots In the special case that f is a. B) show that a polynomial of degree n has at most n real. here’s how descartes’s rule of signs can give you the numbers of possible real roots, both positive and negative: a) show that a polynomial of degree 3 has at most three real roots. Use the rational root. How To Prove Real Roots.
From www.youtube.com
Showing that a Function Has Exactly One Root YouTube How To Prove Real Roots to prove existence of roots of a continuous function, you can exhibit changes of sign. follow these general steps to ensure that you find every root: find the real roots of each equation by factoring or using the quadratic formula. whether the discriminant is greater than zero, equal to zero or less than zero can be. How To Prove Real Roots.
From www.coursehero.com
[Solved] Show that the equation has exactly one real root. x 3 + e x = 0 Course Hero How To Prove Real Roots a) show that a polynomial of degree 3 has at most three real roots. B) show that a polynomial of degree n has at most n real. whether the discriminant is greater than zero, equal to zero or less than zero can be used to determine if a quadratic equation has no real roots, real and equal. . How To Prove Real Roots.
From rootsbq.blogspot.com
How To Find The Root Of An Equation ROOTSB How To Prove Real Roots find the real roots of each equation by factoring or using the quadratic formula. to prove existence of roots of a continuous function, you can exhibit changes of sign. here’s how descartes’s rule of signs can give you the numbers of possible real roots, both positive and negative: Use the rational root theorem to list all possible. How To Prove Real Roots.
From www.youtube.com
LC HL prove the roots of the quadratic equation are real and express these roots in terms of K How To Prove Real Roots whether the discriminant is greater than zero, equal to zero or less than zero can be used to determine if a quadratic equation has no real roots, real and equal. In the special case that f is a. in your example, computing f(±2) = 3 and f(0) = −1 gives that f has one root each in (−2,. How To Prove Real Roots.
From www.youtube.com
POL.4A &B Real and Complex Roots from Graphs YouTube How To Prove Real Roots follow these general steps to ensure that you find every root: here’s how descartes’s rule of signs can give you the numbers of possible real roots, both positive and negative: to prove existence of roots of a continuous function, you can exhibit changes of sign. find the real roots of each equation by factoring or using. How To Prove Real Roots.
From www.youtube.com
Prove the equation has at least one real root (KristaKingMath) YouTube How To Prove Real Roots In the special case that f is a. B) show that a polynomial of degree n has at most n real. follow these general steps to ensure that you find every root: find the real roots of each equation by factoring or using the quadratic formula. here’s how descartes’s rule of signs can give you the numbers. How To Prove Real Roots.
From slidetodoc.com
Finding Real Roots of Polynomial Equations How do How To Prove Real Roots here’s how descartes’s rule of signs can give you the numbers of possible real roots, both positive and negative: follow these general steps to ensure that you find every root: to prove existence of roots of a continuous function, you can exhibit changes of sign. find the real roots of each equation by factoring or using. How To Prove Real Roots.
From www.slideshare.net
Roots of real numbers and radical expressions How To Prove Real Roots whether the discriminant is greater than zero, equal to zero or less than zero can be used to determine if a quadratic equation has no real roots, real and equal. a) show that a polynomial of degree 3 has at most three real roots. find the real roots of each equation by factoring or using the quadratic. How To Prove Real Roots.
From www.slideserve.com
PPT Proof of the formula for the roots of quadratic equation ax 2 + bx + c = 0 PowerPoint How To Prove Real Roots follow these general steps to ensure that you find every root: Use the rational root theorem to list all possible rational roots. in your example, computing f(±2) = 3 and f(0) = −1 gives that f has one root each in (−2, 0) and (0, +2). whether the discriminant is greater than zero, equal to zero or. How To Prove Real Roots.
From www.numerade.com
SOLVED4344= (a) Prove that the equation has at least one real root (b) Use your calculator to How To Prove Real Roots find the real roots of each equation by factoring or using the quadratic formula. whether the discriminant is greater than zero, equal to zero or less than zero can be used to determine if a quadratic equation has no real roots, real and equal. in your example, computing f(±2) = 3 and f(0) = −1 gives that. How To Prove Real Roots.
From www.youtube.com
How to prove that the function has exactly one real root YouTube How To Prove Real Roots find the real roots of each equation by factoring or using the quadratic formula. here’s how descartes’s rule of signs can give you the numbers of possible real roots, both positive and negative: follow these general steps to ensure that you find every root: In the special case that f is a. whether the discriminant is. How To Prove Real Roots.
From www.onlinemathlearning.com
Rational Root Theorem (examples, solutions, worksheets, videos, activities) How To Prove Real Roots here’s how descartes’s rule of signs can give you the numbers of possible real roots, both positive and negative: to prove existence of roots of a continuous function, you can exhibit changes of sign. in your example, computing f(±2) = 3 and f(0) = −1 gives that f has one root each in (−2, 0) and (0,. How To Prove Real Roots.
From www.youtube.com
Rolle's Theorem to Prove Exactly one root for Cubic Function AP Calculus YouTube How To Prove Real Roots a) show that a polynomial of degree 3 has at most three real roots. Use the rational root theorem to list all possible rational roots. B) show that a polynomial of degree n has at most n real. In the special case that f is a. find the real roots of each equation by factoring or using the. How To Prove Real Roots.
From www.youtube.com
Show that the equation has at least one real root. YouTube How To Prove Real Roots Use the rational root theorem to list all possible rational roots. In the special case that f is a. B) show that a polynomial of degree n has at most n real. follow these general steps to ensure that you find every root: to prove existence of roots of a continuous function, you can exhibit changes of sign.. How To Prove Real Roots.
From prince-blogstone.blogspot.com
How to Determine How Many Real Roots a Polynomial Has How To Prove Real Roots find the real roots of each equation by factoring or using the quadratic formula. follow these general steps to ensure that you find every root: Use the rational root theorem to list all possible rational roots. a) show that a polynomial of degree 3 has at most three real roots. whether the discriminant is greater than. How To Prove Real Roots.
From www.youtube.com
Real and Complex Polynomial Roots YouTube How To Prove Real Roots find the real roots of each equation by factoring or using the quadratic formula. B) show that a polynomial of degree n has at most n real. in your example, computing f(±2) = 3 and f(0) = −1 gives that f has one root each in (−2, 0) and (0, +2). Use the rational root theorem to list. How To Prove Real Roots.
From www.youtube.com
57. (a) Prove that the equation has at least one real root.(b) Use your calculator to find an How To Prove Real Roots Use the rational root theorem to list all possible rational roots. follow these general steps to ensure that you find every root: In the special case that f is a. to prove existence of roots of a continuous function, you can exhibit changes of sign. in your example, computing f(±2) = 3 and f(0) = −1 gives. How To Prove Real Roots.
From www.slideserve.com
PPT Fundamental Theorem of Algebra and Finding Real Roots PowerPoint Presentation ID2666595 How To Prove Real Roots here’s how descartes’s rule of signs can give you the numbers of possible real roots, both positive and negative: find the real roots of each equation by factoring or using the quadratic formula. B) show that a polynomial of degree n has at most n real. in your example, computing f(±2) = 3 and f(0) = −1. How To Prove Real Roots.
From ar.inspiredpencil.com
Real Roots Math How To Prove Real Roots Use the rational root theorem to list all possible rational roots. a) show that a polynomial of degree 3 has at most three real roots. whether the discriminant is greater than zero, equal to zero or less than zero can be used to determine if a quadratic equation has no real roots, real and equal. in your. How To Prove Real Roots.
From www.slideserve.com
PPT Section 35 Finding Real Roots of Polynomial Equations PowerPoint Presentation ID2571687 How To Prove Real Roots here’s how descartes’s rule of signs can give you the numbers of possible real roots, both positive and negative: a) show that a polynomial of degree 3 has at most three real roots. to prove existence of roots of a continuous function, you can exhibit changes of sign. in your example, computing f(±2) = 3 and. How To Prove Real Roots.
From www.youtube.com
Show that the following equation has a real root. YouTube How To Prove Real Roots a) show that a polynomial of degree 3 has at most three real roots. here’s how descartes’s rule of signs can give you the numbers of possible real roots, both positive and negative: Use the rational root theorem to list all possible rational roots. find the real roots of each equation by factoring or using the quadratic. How To Prove Real Roots.
From www.youtube.com
Characteristic Equation 3 Real Roots YouTube How To Prove Real Roots find the real roots of each equation by factoring or using the quadratic formula. here’s how descartes’s rule of signs can give you the numbers of possible real roots, both positive and negative: B) show that a polynomial of degree n has at most n real. In the special case that f is a. follow these general. How To Prove Real Roots.
From www.youtube.com
Finding Real Roots YouTube How To Prove Real Roots a) show that a polynomial of degree 3 has at most three real roots. find the real roots of each equation by factoring or using the quadratic formula. follow these general steps to ensure that you find every root: B) show that a polynomial of degree n has at most n real. whether the discriminant is. How To Prove Real Roots.