Disks And Washers Versus Cylindrical Shells at Harrison Logic blog

Disks And Washers Versus Cylindrical Shells. For example, consider the region. In general, the shell method is easier to use when the solid of. With the disk/washer method, the area is made up of a series of stacked disks. The disk washer method and the cylindrical. So far, we have used disks and washers to find volumes. A method of calculating the volume of a solid of revolution by dividing the solid into nested cylindrical shells; With the shell method, the area is made up of nested. It is very short, but the. However, each method has its own strengths and weaknesses. Find the volume of the solid that is produced when the region bounded by the curve. Y = x2, y = 0, and x = 2. A washer is like a washer that you would see in a hardware store. When the solid of revolution has a cavity in the middle, the slices used to approximate the volume are not disks, but washers (disks with holes in the center). This method is different from the methods of disks or washers in that we integrate with respect to the opposite variable There are two ways to find the volume of three dimensional objects in calculus:

The disk washer method and the cylindrical. With the disk/washer method, the area is made up of a series of stacked disks. A method of calculating the volume of a solid of revolution by dividing the solid into nested cylindrical shells; This method is different from the methods of disks or washers in that we integrate with respect to the opposite variable With the shell method, the area is made up of nested. However, each method has its own strengths and weaknesses. Find the volume of the solid that is produced when the region bounded by the curve. In general, the shell method is easier to use when the solid of. A washer is like a washer that you would see in a hardware store. For example, consider the region.

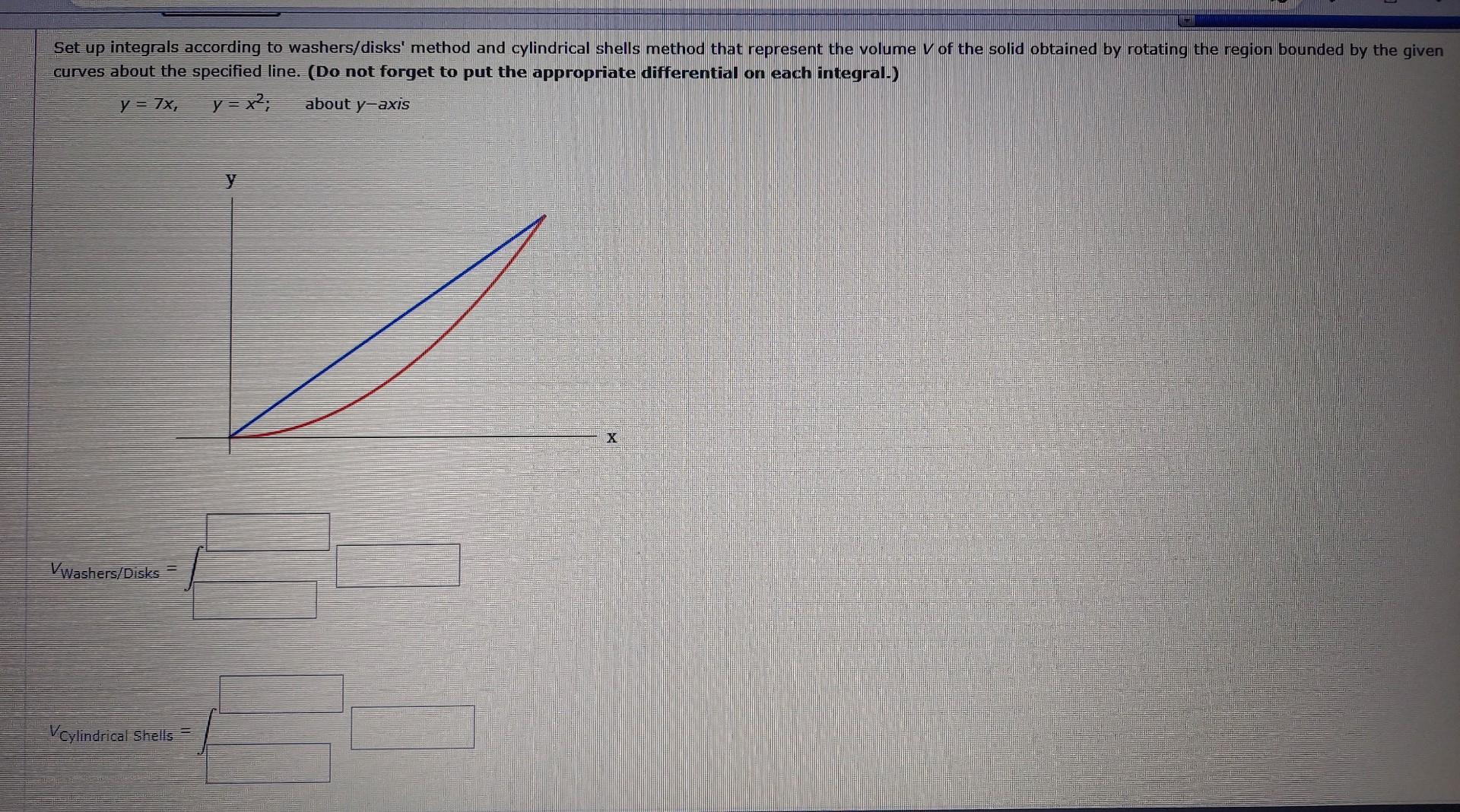
Solved Set up integrals according to washers/disks' method

Disks And Washers Versus Cylindrical Shells However, each method has its own strengths and weaknesses. A method of calculating the volume of a solid of revolution by dividing the solid into nested cylindrical shells; In general, the shell method is easier to use when the solid of. There are two ways to find the volume of three dimensional objects in calculus: Y = x2, y = 0, and x = 2. For example, consider the region. This method is different from the methods of disks or washers in that we integrate with respect to the opposite variable It is very short, but the. So far, we have used disks and washers to find volumes. When the solid of revolution has a cavity in the middle, the slices used to approximate the volume are not disks, but washers (disks with holes in the center). A washer is like a washer that you would see in a hardware store. With the disk/washer method, the area is made up of a series of stacked disks. The disk washer method and the cylindrical. However, each method has its own strengths and weaknesses. Find the volume of the solid that is produced when the region bounded by the curve. With the shell method, the area is made up of nested.