Prove That Sphere Is A Convex at Alexander Hickson blog

Prove That Sphere Is A Convex. Convexity, or convex analysis, is an area of mathematics where one studies questions related to two basic objects, namely convex sets and. R), that is, k x. Define the open and closed ball. An open ball in the metric induced by ∥⋅∥ ‖ ⋅ ‖. Let x x be a normed linear space, x ∈ x x ∈ x and r> 0 r> 0. Indeed, suppose that x;y 2 c(x0; R is equipped with the euclidean norm. R) r is convex, where n. Let v v be a normed vector space with norm ∥⋅∥ ‖ ⋅ ‖ over r r or c c. I can prove with the triangle inequality that the unit sphere in $r^n$ is convex, but how to show that it is strictly convex? After central projection on the plane (klein model for sphere) you obtain usual ellipse. Proving that closed (and open) balls are convex. An open sphere n c(x0; Also you can show it using. We prove several sharp distortion and monotonicity theorems for spherically convex functions defined on the unit disk involving.

R), that is, k x. R is equipped with the euclidean norm. Indeed, suppose that x;y 2 c(x0; I can prove with the triangle inequality that the unit sphere in $r^n$ is convex, but how to show that it is strictly convex? After central projection on the plane (klein model for sphere) you obtain usual ellipse. An open ball in the metric induced by ∥⋅∥ ‖ ⋅ ‖. We prove several sharp distortion and monotonicity theorems for spherically convex functions defined on the unit disk involving. Define the open and closed ball. Proving that closed (and open) balls are convex. Let v v be a normed vector space with norm ∥⋅∥ ‖ ⋅ ‖ over r r or c c.

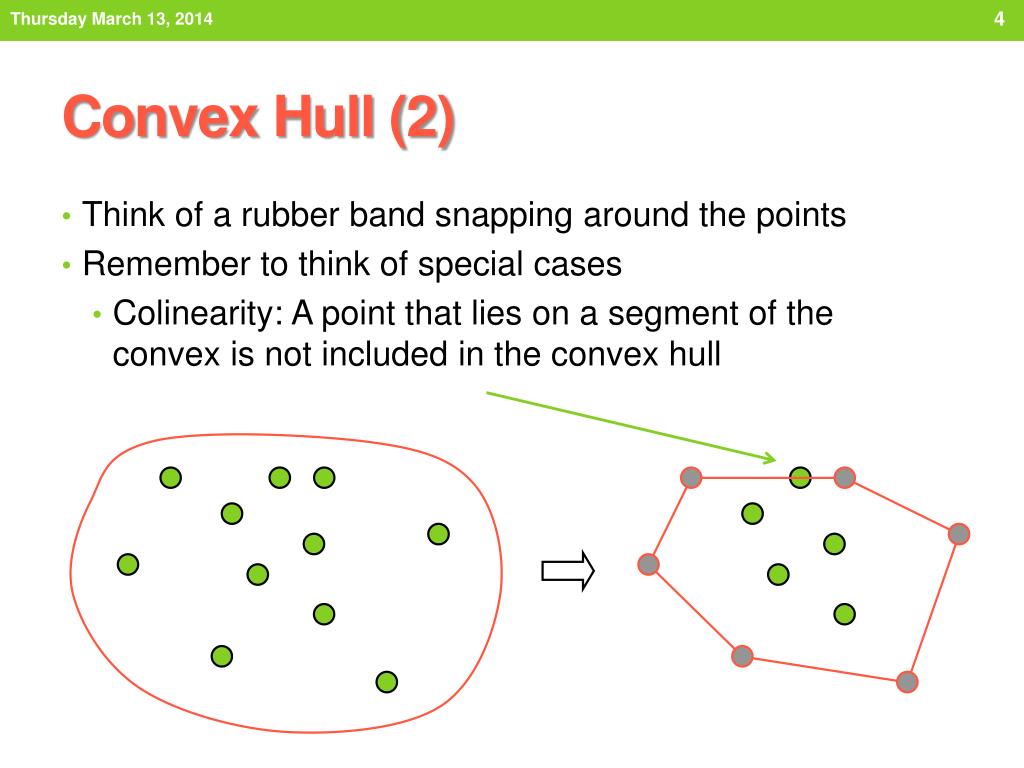
PPT Convex Hull PowerPoint Presentation, free download ID2263696

Prove That Sphere Is A Convex Proving that closed (and open) balls are convex. R), that is, k x. Let x x be a normed linear space, x ∈ x x ∈ x and r> 0 r> 0. Indeed, suppose that x;y 2 c(x0; Let v v be a normed vector space with norm ∥⋅∥ ‖ ⋅ ‖ over r r or c c. R) r is convex, where n. We prove several sharp distortion and monotonicity theorems for spherically convex functions defined on the unit disk involving. An open sphere n c(x0; Proving that closed (and open) balls are convex. R is equipped with the euclidean norm. Also you can show it using. I can prove with the triangle inequality that the unit sphere in $r^n$ is convex, but how to show that it is strictly convex? Define the open and closed ball. An open ball in the metric induced by ∥⋅∥ ‖ ⋅ ‖. Convexity, or convex analysis, is an area of mathematics where one studies questions related to two basic objects, namely convex sets and. After central projection on the plane (klein model for sphere) you obtain usual ellipse.