What Is The Definition Of Inverse In Geometry . A branch of mathematics focusing on figures unchanged by inversion, using inversion circles as a. If a conditional statement is \(p\rightarrow q\), then the inverse is \(\sim p\rightarrow \sim q\). Inverse is a statement formed by negating the hypothesis and conclusion of the original conditional. The inverse of the conditional \(p \rightarrow q\) is \(\neg p \rightarrow \neg q\text{.}\) the contrapositive of this new conditional is \(\neg. Inversion offers a way to reflect points across a circle. This concept introduces students to converses, inverses, contrapositives, and biconditional statements. Inversion is the process of transforming points p to a corresponding set of points p^' known as their inverse points. Two points p and p^' are said to be inverses with respect to an.
from helpingwithmath.com
Two points p and p^' are said to be inverses with respect to an. A branch of mathematics focusing on figures unchanged by inversion, using inversion circles as a. This concept introduces students to converses, inverses, contrapositives, and biconditional statements. Inverse is a statement formed by negating the hypothesis and conclusion of the original conditional. Inversion offers a way to reflect points across a circle. The inverse of the conditional \(p \rightarrow q\) is \(\neg p \rightarrow \neg q\text{.}\) the contrapositive of this new conditional is \(\neg. Inversion is the process of transforming points p to a corresponding set of points p^' known as their inverse points. If a conditional statement is \(p\rightarrow q\), then the inverse is \(\sim p\rightarrow \sim q\).
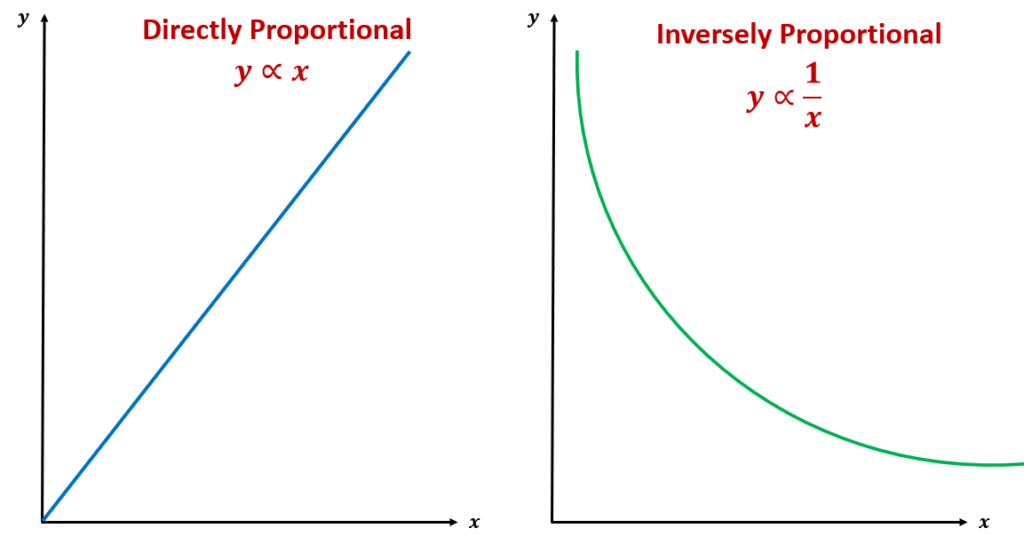
Inverse Proportion Definition, Examples, Graph, Formula
What Is The Definition Of Inverse In Geometry This concept introduces students to converses, inverses, contrapositives, and biconditional statements. This concept introduces students to converses, inverses, contrapositives, and biconditional statements. If a conditional statement is \(p\rightarrow q\), then the inverse is \(\sim p\rightarrow \sim q\). Two points p and p^' are said to be inverses with respect to an. A branch of mathematics focusing on figures unchanged by inversion, using inversion circles as a. The inverse of the conditional \(p \rightarrow q\) is \(\neg p \rightarrow \neg q\text{.}\) the contrapositive of this new conditional is \(\neg. Inversion offers a way to reflect points across a circle. Inverse is a statement formed by negating the hypothesis and conclusion of the original conditional. Inversion is the process of transforming points p to a corresponding set of points p^' known as their inverse points.
From helpingwithmath.com
Inverse Proportion Definition, Examples, Graph, Formula What Is The Definition Of Inverse In Geometry Inversion is the process of transforming points p to a corresponding set of points p^' known as their inverse points. Two points p and p^' are said to be inverses with respect to an. The inverse of the conditional \(p \rightarrow q\) is \(\neg p \rightarrow \neg q\text{.}\) the contrapositive of this new conditional is \(\neg. Inverse is a statement. What Is The Definition Of Inverse In Geometry.
From www.storyofmathematics.com
Inverse of a Function Explanation & Examples What Is The Definition Of Inverse In Geometry Inverse is a statement formed by negating the hypothesis and conclusion of the original conditional. Inversion offers a way to reflect points across a circle. A branch of mathematics focusing on figures unchanged by inversion, using inversion circles as a. The inverse of the conditional \(p \rightarrow q\) is \(\neg p \rightarrow \neg q\text{.}\) the contrapositive of this new conditional. What Is The Definition Of Inverse In Geometry.
From www.youtube.com
Introduction to Inverse Functions YouTube What Is The Definition Of Inverse In Geometry Inverse is a statement formed by negating the hypothesis and conclusion of the original conditional. A branch of mathematics focusing on figures unchanged by inversion, using inversion circles as a. If a conditional statement is \(p\rightarrow q\), then the inverse is \(\sim p\rightarrow \sim q\). This concept introduces students to converses, inverses, contrapositives, and biconditional statements. Inversion offers a way. What Is The Definition Of Inverse In Geometry.
From mathoriginal.com
Inverse Functions Math Original What Is The Definition Of Inverse In Geometry Inversion offers a way to reflect points across a circle. Inversion is the process of transforming points p to a corresponding set of points p^' known as their inverse points. The inverse of the conditional \(p \rightarrow q\) is \(\neg p \rightarrow \neg q\text{.}\) the contrapositive of this new conditional is \(\neg. This concept introduces students to converses, inverses, contrapositives,. What Is The Definition Of Inverse In Geometry.
From formulainmaths.in
Inverse Trigonometric Functions Formula For 12th Class » Formula In Maths What Is The Definition Of Inverse In Geometry This concept introduces students to converses, inverses, contrapositives, and biconditional statements. Inversion is the process of transforming points p to a corresponding set of points p^' known as their inverse points. Two points p and p^' are said to be inverses with respect to an. Inversion offers a way to reflect points across a circle. A branch of mathematics focusing. What Is The Definition Of Inverse In Geometry.
From quizdbbarnstorms.z21.web.core.windows.net
Whats An Inverse Relationship What Is The Definition Of Inverse In Geometry Two points p and p^' are said to be inverses with respect to an. The inverse of the conditional \(p \rightarrow q\) is \(\neg p \rightarrow \neg q\text{.}\) the contrapositive of this new conditional is \(\neg. Inversion offers a way to reflect points across a circle. If a conditional statement is \(p\rightarrow q\), then the inverse is \(\sim p\rightarrow \sim. What Is The Definition Of Inverse In Geometry.
From www.storyofmathematics.com
Inverse Definition & Meaning What Is The Definition Of Inverse In Geometry Inverse is a statement formed by negating the hypothesis and conclusion of the original conditional. If a conditional statement is \(p\rightarrow q\), then the inverse is \(\sim p\rightarrow \sim q\). The inverse of the conditional \(p \rightarrow q\) is \(\neg p \rightarrow \neg q\text{.}\) the contrapositive of this new conditional is \(\neg. This concept introduces students to converses, inverses, contrapositives,. What Is The Definition Of Inverse In Geometry.
From slideplayer.com
Trigonometric Inverses ppt download What Is The Definition Of Inverse In Geometry Inversion is the process of transforming points p to a corresponding set of points p^' known as their inverse points. Inversion offers a way to reflect points across a circle. Two points p and p^' are said to be inverses with respect to an. The inverse of the conditional \(p \rightarrow q\) is \(\neg p \rightarrow \neg q\text{.}\) the contrapositive. What Is The Definition Of Inverse In Geometry.
From mr-mathematics.com
Differentiating Inverse Trigonometric Functions What Is The Definition Of Inverse In Geometry Inversion offers a way to reflect points across a circle. If a conditional statement is \(p\rightarrow q\), then the inverse is \(\sim p\rightarrow \sim q\). Inversion is the process of transforming points p to a corresponding set of points p^' known as their inverse points. Inverse is a statement formed by negating the hypothesis and conclusion of the original conditional.. What Is The Definition Of Inverse In Geometry.
From www.ck12.org
Inverse Matrices Overview ( Video ) Algebra CK12 Foundation What Is The Definition Of Inverse In Geometry Inversion is the process of transforming points p to a corresponding set of points p^' known as their inverse points. Two points p and p^' are said to be inverses with respect to an. Inverse is a statement formed by negating the hypothesis and conclusion of the original conditional. Inversion offers a way to reflect points across a circle. If. What Is The Definition Of Inverse In Geometry.
From www.youtube.com
Inverse Trig Functions Review of Trigonometry IB Physics YouTube What Is The Definition Of Inverse In Geometry Inverse is a statement formed by negating the hypothesis and conclusion of the original conditional. If a conditional statement is \(p\rightarrow q\), then the inverse is \(\sim p\rightarrow \sim q\). This concept introduces students to converses, inverses, contrapositives, and biconditional statements. A branch of mathematics focusing on figures unchanged by inversion, using inversion circles as a. Inversion is the process. What Is The Definition Of Inverse In Geometry.
From spmaddmaths.blog.onlinetuition.com.my
Inverse Function Example 1 SPM Additional Mathematics What Is The Definition Of Inverse In Geometry Inversion offers a way to reflect points across a circle. Inverse is a statement formed by negating the hypothesis and conclusion of the original conditional. A branch of mathematics focusing on figures unchanged by inversion, using inversion circles as a. If a conditional statement is \(p\rightarrow q\), then the inverse is \(\sim p\rightarrow \sim q\). This concept introduces students to. What Is The Definition Of Inverse In Geometry.
From www.youtube.com
How to find the inverse of a function example YouTube What Is The Definition Of Inverse In Geometry If a conditional statement is \(p\rightarrow q\), then the inverse is \(\sim p\rightarrow \sim q\). Two points p and p^' are said to be inverses with respect to an. Inversion is the process of transforming points p to a corresponding set of points p^' known as their inverse points. Inversion offers a way to reflect points across a circle. This. What Is The Definition Of Inverse In Geometry.
From www.slideserve.com
PPT 1.4c Inverse Relations and Inverse Functions PowerPoint What Is The Definition Of Inverse In Geometry Two points p and p^' are said to be inverses with respect to an. Inversion offers a way to reflect points across a circle. Inversion is the process of transforming points p to a corresponding set of points p^' known as their inverse points. If a conditional statement is \(p\rightarrow q\), then the inverse is \(\sim p\rightarrow \sim q\). The. What Is The Definition Of Inverse In Geometry.
From thirdspacelearning.com
Inverse Functions GCSE Maths Steps, Examples & Worksheet What Is The Definition Of Inverse In Geometry The inverse of the conditional \(p \rightarrow q\) is \(\neg p \rightarrow \neg q\text{.}\) the contrapositive of this new conditional is \(\neg. Inverse is a statement formed by negating the hypothesis and conclusion of the original conditional. A branch of mathematics focusing on figures unchanged by inversion, using inversion circles as a. If a conditional statement is \(p\rightarrow q\), then. What Is The Definition Of Inverse In Geometry.
From www.youtube.com
Inverse Functions Understand in 10 Minutes YouTube What Is The Definition Of Inverse In Geometry Inversion is the process of transforming points p to a corresponding set of points p^' known as their inverse points. This concept introduces students to converses, inverses, contrapositives, and biconditional statements. A branch of mathematics focusing on figures unchanged by inversion, using inversion circles as a. The inverse of the conditional \(p \rightarrow q\) is \(\neg p \rightarrow \neg q\text{.}\). What Is The Definition Of Inverse In Geometry.
From www.youtube.com
Precalculus 408 Inverse Trigonometric Functions YouTube What Is The Definition Of Inverse In Geometry This concept introduces students to converses, inverses, contrapositives, and biconditional statements. If a conditional statement is \(p\rightarrow q\), then the inverse is \(\sim p\rightarrow \sim q\). A branch of mathematics focusing on figures unchanged by inversion, using inversion circles as a. Two points p and p^' are said to be inverses with respect to an. Inverse is a statement formed. What Is The Definition Of Inverse In Geometry.
From www.cuemath.com
Inverse Trigonometric Ratios Formulas, Definition, Properties, Solved What Is The Definition Of Inverse In Geometry This concept introduces students to converses, inverses, contrapositives, and biconditional statements. Inversion is the process of transforming points p to a corresponding set of points p^' known as their inverse points. Inversion offers a way to reflect points across a circle. Two points p and p^' are said to be inverses with respect to an. A branch of mathematics focusing. What Is The Definition Of Inverse In Geometry.
From people.math.carleton.ca
Inverse functions What Is The Definition Of Inverse In Geometry If a conditional statement is \(p\rightarrow q\), then the inverse is \(\sim p\rightarrow \sim q\). Inverse is a statement formed by negating the hypothesis and conclusion of the original conditional. Inversion offers a way to reflect points across a circle. A branch of mathematics focusing on figures unchanged by inversion, using inversion circles as a. The inverse of the conditional. What Is The Definition Of Inverse In Geometry.
From www.slideserve.com
PPT 1.4c Inverse Relations and Inverse Functions PowerPoint What Is The Definition Of Inverse In Geometry Two points p and p^' are said to be inverses with respect to an. Inversion offers a way to reflect points across a circle. Inversion is the process of transforming points p to a corresponding set of points p^' known as their inverse points. Inverse is a statement formed by negating the hypothesis and conclusion of the original conditional. A. What Is The Definition Of Inverse In Geometry.
From www.youtube.com
How to Find an Inverse Relation an Equation Algebra 2 Math Video What Is The Definition Of Inverse In Geometry This concept introduces students to converses, inverses, contrapositives, and biconditional statements. Inversion offers a way to reflect points across a circle. If a conditional statement is \(p\rightarrow q\), then the inverse is \(\sim p\rightarrow \sim q\). The inverse of the conditional \(p \rightarrow q\) is \(\neg p \rightarrow \neg q\text{.}\) the contrapositive of this new conditional is \(\neg. Inversion is. What Is The Definition Of Inverse In Geometry.
From www.media4math.com
DefinitionGeometry BasicsInverse Statement Media4Math What Is The Definition Of Inverse In Geometry This concept introduces students to converses, inverses, contrapositives, and biconditional statements. Two points p and p^' are said to be inverses with respect to an. Inverse is a statement formed by negating the hypothesis and conclusion of the original conditional. Inversion offers a way to reflect points across a circle. If a conditional statement is \(p\rightarrow q\), then the inverse. What Is The Definition Of Inverse In Geometry.
From www.vrogue.co
What Are Inverse Operations Definition Facts And Exam vrogue.co What Is The Definition Of Inverse In Geometry This concept introduces students to converses, inverses, contrapositives, and biconditional statements. Inversion offers a way to reflect points across a circle. The inverse of the conditional \(p \rightarrow q\) is \(\neg p \rightarrow \neg q\text{.}\) the contrapositive of this new conditional is \(\neg. Two points p and p^' are said to be inverses with respect to an. Inversion is the. What Is The Definition Of Inverse In Geometry.
From telgurus.co.uk
What is an Inverse function? Definition, Examples, method What Is The Definition Of Inverse In Geometry Inverse is a statement formed by negating the hypothesis and conclusion of the original conditional. Inversion offers a way to reflect points across a circle. The inverse of the conditional \(p \rightarrow q\) is \(\neg p \rightarrow \neg q\text{.}\) the contrapositive of this new conditional is \(\neg. Two points p and p^' are said to be inverses with respect to. What Is The Definition Of Inverse In Geometry.
From www.youtube.com
Definition of the Inverse of a Function YouTube What Is The Definition Of Inverse In Geometry If a conditional statement is \(p\rightarrow q\), then the inverse is \(\sim p\rightarrow \sim q\). A branch of mathematics focusing on figures unchanged by inversion, using inversion circles as a. Inverse is a statement formed by negating the hypothesis and conclusion of the original conditional. Inversion offers a way to reflect points across a circle. Two points p and p^'. What Is The Definition Of Inverse In Geometry.
From owlcation.com
How to Find the Inverse of a Function (With Examples) Owlcation What Is The Definition Of Inverse In Geometry Inverse is a statement formed by negating the hypothesis and conclusion of the original conditional. Inversion is the process of transforming points p to a corresponding set of points p^' known as their inverse points. Inversion offers a way to reflect points across a circle. This concept introduces students to converses, inverses, contrapositives, and biconditional statements. The inverse of the. What Is The Definition Of Inverse In Geometry.
From www.youtube.com
Inverse Trigonometric Ratios Lesson (Basic Geometry Concepts) YouTube What Is The Definition Of Inverse In Geometry Two points p and p^' are said to be inverses with respect to an. If a conditional statement is \(p\rightarrow q\), then the inverse is \(\sim p\rightarrow \sim q\). The inverse of the conditional \(p \rightarrow q\) is \(\neg p \rightarrow \neg q\text{.}\) the contrapositive of this new conditional is \(\neg. A branch of mathematics focusing on figures unchanged by. What Is The Definition Of Inverse In Geometry.
From www.slideserve.com
PPT Discrete Mathematics Functions PowerPoint Presentation, free What Is The Definition Of Inverse In Geometry The inverse of the conditional \(p \rightarrow q\) is \(\neg p \rightarrow \neg q\text{.}\) the contrapositive of this new conditional is \(\neg. Inverse is a statement formed by negating the hypothesis and conclusion of the original conditional. Inversion is the process of transforming points p to a corresponding set of points p^' known as their inverse points. A branch of. What Is The Definition Of Inverse In Geometry.
From www.aplustopper.com
Definition of Inverse Function A Plus Topper What Is The Definition Of Inverse In Geometry A branch of mathematics focusing on figures unchanged by inversion, using inversion circles as a. Inversion is the process of transforming points p to a corresponding set of points p^' known as their inverse points. If a conditional statement is \(p\rightarrow q\), then the inverse is \(\sim p\rightarrow \sim q\). This concept introduces students to converses, inverses, contrapositives, and biconditional. What Is The Definition Of Inverse In Geometry.
From formulainmaths.in
Inverse Circular Function Formula » Formula In Maths What Is The Definition Of Inverse In Geometry Two points p and p^' are said to be inverses with respect to an. Inverse is a statement formed by negating the hypothesis and conclusion of the original conditional. Inversion is the process of transforming points p to a corresponding set of points p^' known as their inverse points. If a conditional statement is \(p\rightarrow q\), then the inverse is. What Is The Definition Of Inverse In Geometry.
From mungfali.com
What Is An Inverse What Is The Definition Of Inverse In Geometry Inversion is the process of transforming points p to a corresponding set of points p^' known as their inverse points. Inverse is a statement formed by negating the hypothesis and conclusion of the original conditional. Inversion offers a way to reflect points across a circle. The inverse of the conditional \(p \rightarrow q\) is \(\neg p \rightarrow \neg q\text{.}\) the. What Is The Definition Of Inverse In Geometry.
From www.youtube.com
Converse, Inverse, & Contrapositive Conditional & Biconditional What Is The Definition Of Inverse In Geometry The inverse of the conditional \(p \rightarrow q\) is \(\neg p \rightarrow \neg q\text{.}\) the contrapositive of this new conditional is \(\neg. A branch of mathematics focusing on figures unchanged by inversion, using inversion circles as a. Inversion is the process of transforming points p to a corresponding set of points p^' known as their inverse points. This concept introduces. What Is The Definition Of Inverse In Geometry.
From www.youtube.com
Definition of Inverse Functions and Logarithms YouTube What Is The Definition Of Inverse In Geometry The inverse of the conditional \(p \rightarrow q\) is \(\neg p \rightarrow \neg q\text{.}\) the contrapositive of this new conditional is \(\neg. Inversion offers a way to reflect points across a circle. This concept introduces students to converses, inverses, contrapositives, and biconditional statements. If a conditional statement is \(p\rightarrow q\), then the inverse is \(\sim p\rightarrow \sim q\). Inversion is. What Is The Definition Of Inverse In Geometry.
From www.cuemath.com
Inverse Function Formula Learn the Formula to Find the Inverse of a What Is The Definition Of Inverse In Geometry This concept introduces students to converses, inverses, contrapositives, and biconditional statements. Two points p and p^' are said to be inverses with respect to an. Inverse is a statement formed by negating the hypothesis and conclusion of the original conditional. Inversion is the process of transforming points p to a corresponding set of points p^' known as their inverse points.. What Is The Definition Of Inverse In Geometry.
From www.youtube.com
Inverse Trigonometric Ratios YouTube What Is The Definition Of Inverse In Geometry Two points p and p^' are said to be inverses with respect to an. The inverse of the conditional \(p \rightarrow q\) is \(\neg p \rightarrow \neg q\text{.}\) the contrapositive of this new conditional is \(\neg. This concept introduces students to converses, inverses, contrapositives, and biconditional statements. If a conditional statement is \(p\rightarrow q\), then the inverse is \(\sim p\rightarrow. What Is The Definition Of Inverse In Geometry.