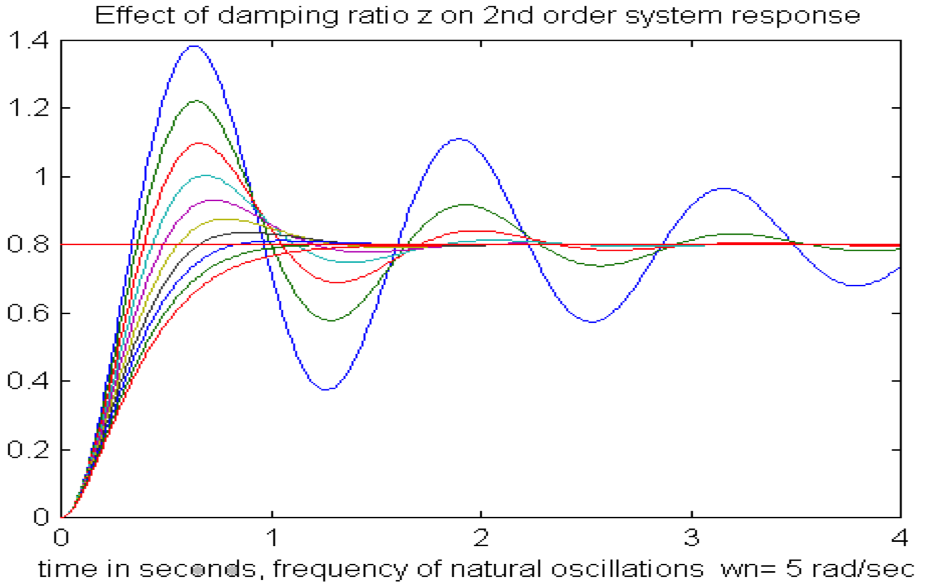
Underdamped Oscillation Formula . Frequency and graph the solution with initial conditions x(0). When the damping constant is small, b < \(\sqrt{4mk}\), the system oscillates while the amplitude of the motion decays exponentially. How do we model oscillatory phenomena in which air drag causes a decrease in oscillation amplitude? When a damped oscillator is underdamped, it approaches zero faster than in the case of critical damping, but oscillates about that zero. Underdamped solutions oscillate rapidly with the frequency and decay envelope described above. Show that the system x + 1x + 3x = 0 is underdamped, find its damped angular. (2) since we have d=beta^2. 1.1 drag and general damping forces.
from pressbooks.library.torontomu.ca
How do we model oscillatory phenomena in which air drag causes a decrease in oscillation amplitude? When the damping constant is small, b < \(\sqrt{4mk}\), the system oscillates while the amplitude of the motion decays exponentially. When a damped oscillator is underdamped, it approaches zero faster than in the case of critical damping, but oscillates about that zero. 1.1 drag and general damping forces. Show that the system x + 1x + 3x = 0 is underdamped, find its damped angular. (2) since we have d=beta^2. Underdamped solutions oscillate rapidly with the frequency and decay envelope described above. Frequency and graph the solution with initial conditions x(0).
7.1 Second Order Underdamped Systems Introduction to Control Systems
Underdamped Oscillation Formula Underdamped solutions oscillate rapidly with the frequency and decay envelope described above. Underdamped solutions oscillate rapidly with the frequency and decay envelope described above. How do we model oscillatory phenomena in which air drag causes a decrease in oscillation amplitude? Frequency and graph the solution with initial conditions x(0). 1.1 drag and general damping forces. When a damped oscillator is underdamped, it approaches zero faster than in the case of critical damping, but oscillates about that zero. When the damping constant is small, b < \(\sqrt{4mk}\), the system oscillates while the amplitude of the motion decays exponentially. (2) since we have d=beta^2. Show that the system x + 1x + 3x = 0 is underdamped, find its damped angular.
From www.slideserve.com
PPT Damped Oscillations PowerPoint Presentation, free download ID Underdamped Oscillation Formula (2) since we have d=beta^2. Underdamped solutions oscillate rapidly with the frequency and decay envelope described above. When a damped oscillator is underdamped, it approaches zero faster than in the case of critical damping, but oscillates about that zero. 1.1 drag and general damping forces. Show that the system x + 1x + 3x = 0 is underdamped, find its. Underdamped Oscillation Formula.
From www.youtube.com
Solution of Differential Equation of Damped Oscillation YouTube Underdamped Oscillation Formula When the damping constant is small, b < \(\sqrt{4mk}\), the system oscillates while the amplitude of the motion decays exponentially. 1.1 drag and general damping forces. Show that the system x + 1x + 3x = 0 is underdamped, find its damped angular. Underdamped solutions oscillate rapidly with the frequency and decay envelope described above. How do we model oscillatory. Underdamped Oscillation Formula.
From www.physicsbootcamp.org
Damping by Resistance Underdamped Oscillation Formula When a damped oscillator is underdamped, it approaches zero faster than in the case of critical damping, but oscillates about that zero. How do we model oscillatory phenomena in which air drag causes a decrease in oscillation amplitude? Show that the system x + 1x + 3x = 0 is underdamped, find its damped angular. (2) since we have d=beta^2.. Underdamped Oscillation Formula.
From www.slideserve.com
PPT Chapter 14 Oscillations PowerPoint Presentation, free download Underdamped Oscillation Formula When the damping constant is small, b < \(\sqrt{4mk}\), the system oscillates while the amplitude of the motion decays exponentially. Underdamped solutions oscillate rapidly with the frequency and decay envelope described above. When a damped oscillator is underdamped, it approaches zero faster than in the case of critical damping, but oscillates about that zero. Show that the system x +. Underdamped Oscillation Formula.
From www.youtube.com
General solution of Underdamped, overdamped, critically damped YouTube Underdamped Oscillation Formula Frequency and graph the solution with initial conditions x(0). 1.1 drag and general damping forces. How do we model oscillatory phenomena in which air drag causes a decrease in oscillation amplitude? Show that the system x + 1x + 3x = 0 is underdamped, find its damped angular. (2) since we have d=beta^2. Underdamped solutions oscillate rapidly with the frequency. Underdamped Oscillation Formula.
From www.slideserve.com
PPT Periodic Motion and Theory of Oscillations PowerPoint Underdamped Oscillation Formula 1.1 drag and general damping forces. Frequency and graph the solution with initial conditions x(0). (2) since we have d=beta^2. When the damping constant is small, b < \(\sqrt{4mk}\), the system oscillates while the amplitude of the motion decays exponentially. How do we model oscillatory phenomena in which air drag causes a decrease in oscillation amplitude? Underdamped solutions oscillate rapidly. Underdamped Oscillation Formula.
From www.houseofmath.com
The Differential Equation for Harmonic Oscillators Underdamped Oscillation Formula Show that the system x + 1x + 3x = 0 is underdamped, find its damped angular. When the damping constant is small, b < \(\sqrt{4mk}\), the system oscillates while the amplitude of the motion decays exponentially. (2) since we have d=beta^2. How do we model oscillatory phenomena in which air drag causes a decrease in oscillation amplitude? Frequency and. Underdamped Oscillation Formula.
From www.youtube.com
Example of Underdamped System Characteristic Equation has Complex Roots Underdamped Oscillation Formula When a damped oscillator is underdamped, it approaches zero faster than in the case of critical damping, but oscillates about that zero. (2) since we have d=beta^2. When the damping constant is small, b < \(\sqrt{4mk}\), the system oscillates while the amplitude of the motion decays exponentially. How do we model oscillatory phenomena in which air drag causes a decrease. Underdamped Oscillation Formula.
From www.youtube.com
Derivation of displacement in damped oscillation, Time period and Underdamped Oscillation Formula How do we model oscillatory phenomena in which air drag causes a decrease in oscillation amplitude? When a damped oscillator is underdamped, it approaches zero faster than in the case of critical damping, but oscillates about that zero. Frequency and graph the solution with initial conditions x(0). Show that the system x + 1x + 3x = 0 is underdamped,. Underdamped Oscillation Formula.
From www.slideserve.com
PPT Chapter 14 Oscillations PowerPoint Presentation, free download Underdamped Oscillation Formula Show that the system x + 1x + 3x = 0 is underdamped, find its damped angular. Underdamped solutions oscillate rapidly with the frequency and decay envelope described above. (2) since we have d=beta^2. When the damping constant is small, b < \(\sqrt{4mk}\), the system oscillates while the amplitude of the motion decays exponentially. 1.1 drag and general damping forces.. Underdamped Oscillation Formula.
From loelnwjph.blob.core.windows.net
Damped Oscillator Energy at Helen Numbers blog Underdamped Oscillation Formula (2) since we have d=beta^2. When a damped oscillator is underdamped, it approaches zero faster than in the case of critical damping, but oscillates about that zero. How do we model oscillatory phenomena in which air drag causes a decrease in oscillation amplitude? Show that the system x + 1x + 3x = 0 is underdamped, find its damped angular.. Underdamped Oscillation Formula.
From www.youtube.com
Harmonic Oscillator (Underdamped) with Periodic Forcing YouTube Underdamped Oscillation Formula (2) since we have d=beta^2. 1.1 drag and general damping forces. Underdamped solutions oscillate rapidly with the frequency and decay envelope described above. Frequency and graph the solution with initial conditions x(0). When a damped oscillator is underdamped, it approaches zero faster than in the case of critical damping, but oscillates about that zero. How do we model oscillatory phenomena. Underdamped Oscillation Formula.
From www.toppr.com
Damped Simple Harmonic Motion Definition, Expression, Example, Video Underdamped Oscillation Formula 1.1 drag and general damping forces. Show that the system x + 1x + 3x = 0 is underdamped, find its damped angular. Underdamped solutions oscillate rapidly with the frequency and decay envelope described above. When the damping constant is small, b < \(\sqrt{4mk}\), the system oscillates while the amplitude of the motion decays exponentially. When a damped oscillator is. Underdamped Oscillation Formula.
From www.researchgate.net
(PDF) Derivation Underdamped Oscillation Formulas by Using Differential Underdamped Oscillation Formula 1.1 drag and general damping forces. When the damping constant is small, b < \(\sqrt{4mk}\), the system oscillates while the amplitude of the motion decays exponentially. How do we model oscillatory phenomena in which air drag causes a decrease in oscillation amplitude? Frequency and graph the solution with initial conditions x(0). Show that the system x + 1x + 3x. Underdamped Oscillation Formula.
From www.slideserve.com
PPT Damped Oscillations PowerPoint Presentation, free download ID Underdamped Oscillation Formula Underdamped solutions oscillate rapidly with the frequency and decay envelope described above. 1.1 drag and general damping forces. Frequency and graph the solution with initial conditions x(0). When a damped oscillator is underdamped, it approaches zero faster than in the case of critical damping, but oscillates about that zero. (2) since we have d=beta^2. How do we model oscillatory phenomena. Underdamped Oscillation Formula.
From engineerexcel.com
Critical Damping Ratio Explained EngineerExcel Underdamped Oscillation Formula When the damping constant is small, b < \(\sqrt{4mk}\), the system oscillates while the amplitude of the motion decays exponentially. 1.1 drag and general damping forces. How do we model oscillatory phenomena in which air drag causes a decrease in oscillation amplitude? Show that the system x + 1x + 3x = 0 is underdamped, find its damped angular. (2). Underdamped Oscillation Formula.
From www.physics.louisville.edu
Damped Oscillations, Forced Oscillations and Resonance Physics 298 Underdamped Oscillation Formula Show that the system x + 1x + 3x = 0 is underdamped, find its damped angular. 1.1 drag and general damping forces. Frequency and graph the solution with initial conditions x(0). Underdamped solutions oscillate rapidly with the frequency and decay envelope described above. When the damping constant is small, b < \(\sqrt{4mk}\), the system oscillates while the amplitude of. Underdamped Oscillation Formula.
From www.pulsedpower.eu
Underdamped solution (δ ω 0 ) Underdamped Oscillation Formula When the damping constant is small, b < \(\sqrt{4mk}\), the system oscillates while the amplitude of the motion decays exponentially. 1.1 drag and general damping forces. Underdamped solutions oscillate rapidly with the frequency and decay envelope described above. When a damped oscillator is underdamped, it approaches zero faster than in the case of critical damping, but oscillates about that zero.. Underdamped Oscillation Formula.
From www.compadre.org
Damped oscillators Nexus Wiki Underdamped Oscillation Formula 1.1 drag and general damping forces. When the damping constant is small, b < \(\sqrt{4mk}\), the system oscillates while the amplitude of the motion decays exponentially. Underdamped solutions oscillate rapidly with the frequency and decay envelope described above. Show that the system x + 1x + 3x = 0 is underdamped, find its damped angular. When a damped oscillator is. Underdamped Oscillation Formula.
From www.nagwa.com
Video Damped Oscillations Nagwa Underdamped Oscillation Formula Show that the system x + 1x + 3x = 0 is underdamped, find its damped angular. How do we model oscillatory phenomena in which air drag causes a decrease in oscillation amplitude? Underdamped solutions oscillate rapidly with the frequency and decay envelope described above. (2) since we have d=beta^2. When the damping constant is small, b < \(\sqrt{4mk}\), the. Underdamped Oscillation Formula.
From www.slideserve.com
PPT Chapter 12 PowerPoint Presentation, free download ID2856172 Underdamped Oscillation Formula Show that the system x + 1x + 3x = 0 is underdamped, find its damped angular. When a damped oscillator is underdamped, it approaches zero faster than in the case of critical damping, but oscillates about that zero. Underdamped solutions oscillate rapidly with the frequency and decay envelope described above. 1.1 drag and general damping forces. Frequency and graph. Underdamped Oscillation Formula.
From physicscourses.colorado.edu
Damped harmonic oscillators Underdamped Oscillation Formula Show that the system x + 1x + 3x = 0 is underdamped, find its damped angular. (2) since we have d=beta^2. When a damped oscillator is underdamped, it approaches zero faster than in the case of critical damping, but oscillates about that zero. When the damping constant is small, b < \(\sqrt{4mk}\), the system oscillates while the amplitude of. Underdamped Oscillation Formula.
From www.researchgate.net
4 solution of the gharmonic oscillator for ζ = 0.5 (underdamped Underdamped Oscillation Formula Show that the system x + 1x + 3x = 0 is underdamped, find its damped angular. How do we model oscillatory phenomena in which air drag causes a decrease in oscillation amplitude? When the damping constant is small, b < \(\sqrt{4mk}\), the system oscillates while the amplitude of the motion decays exponentially. Frequency and graph the solution with initial. Underdamped Oscillation Formula.
From www.houseofmath.com
The Differential Equation for Harmonic Oscillators Underdamped Oscillation Formula When a damped oscillator is underdamped, it approaches zero faster than in the case of critical damping, but oscillates about that zero. Show that the system x + 1x + 3x = 0 is underdamped, find its damped angular. When the damping constant is small, b < \(\sqrt{4mk}\), the system oscillates while the amplitude of the motion decays exponentially. How. Underdamped Oscillation Formula.
From www.researchgate.net
Oscillating solution (underdamped system). Download Scientific Diagram Underdamped Oscillation Formula How do we model oscillatory phenomena in which air drag causes a decrease in oscillation amplitude? When the damping constant is small, b < \(\sqrt{4mk}\), the system oscillates while the amplitude of the motion decays exponentially. (2) since we have d=beta^2. Underdamped solutions oscillate rapidly with the frequency and decay envelope described above. When a damped oscillator is underdamped, it. Underdamped Oscillation Formula.
From www.slideserve.com
PPT Damped Oscillations PowerPoint Presentation, free download ID Underdamped Oscillation Formula (2) since we have d=beta^2. How do we model oscillatory phenomena in which air drag causes a decrease in oscillation amplitude? Underdamped solutions oscillate rapidly with the frequency and decay envelope described above. When the damping constant is small, b < \(\sqrt{4mk}\), the system oscillates while the amplitude of the motion decays exponentially. Frequency and graph the solution with initial. Underdamped Oscillation Formula.
From www.youtube.com
Underdamped system Derivation of equation of motion Damped free Underdamped Oscillation Formula Show that the system x + 1x + 3x = 0 is underdamped, find its damped angular. Underdamped solutions oscillate rapidly with the frequency and decay envelope described above. When a damped oscillator is underdamped, it approaches zero faster than in the case of critical damping, but oscillates about that zero. Frequency and graph the solution with initial conditions x(0).. Underdamped Oscillation Formula.
From www.slideserve.com
PPT Chapter 14 PowerPoint Presentation, free download ID5658621 Underdamped Oscillation Formula Frequency and graph the solution with initial conditions x(0). Underdamped solutions oscillate rapidly with the frequency and decay envelope described above. How do we model oscillatory phenomena in which air drag causes a decrease in oscillation amplitude? When a damped oscillator is underdamped, it approaches zero faster than in the case of critical damping, but oscillates about that zero. When. Underdamped Oscillation Formula.
From www.youtube.com
Damped Oscillations YouTube Underdamped Oscillation Formula 1.1 drag and general damping forces. Show that the system x + 1x + 3x = 0 is underdamped, find its damped angular. When a damped oscillator is underdamped, it approaches zero faster than in the case of critical damping, but oscillates about that zero. How do we model oscillatory phenomena in which air drag causes a decrease in oscillation. Underdamped Oscillation Formula.
From www.slideserve.com
PPT Underdamped Harmonic Oscillator PowerPoint Presentation, free Underdamped Oscillation Formula When the damping constant is small, b < \(\sqrt{4mk}\), the system oscillates while the amplitude of the motion decays exponentially. Underdamped solutions oscillate rapidly with the frequency and decay envelope described above. (2) since we have d=beta^2. How do we model oscillatory phenomena in which air drag causes a decrease in oscillation amplitude? When a damped oscillator is underdamped, it. Underdamped Oscillation Formula.
From math.stackexchange.com
ordinary differential equations Envelope of xt graph in Damped Underdamped Oscillation Formula When a damped oscillator is underdamped, it approaches zero faster than in the case of critical damping, but oscillates about that zero. 1.1 drag and general damping forces. Show that the system x + 1x + 3x = 0 is underdamped, find its damped angular. When the damping constant is small, b < \(\sqrt{4mk}\), the system oscillates while the amplitude. Underdamped Oscillation Formula.
From www.slideserve.com
PPT Chapter 13 Oscillatory Motions PowerPoint Presentation, free Underdamped Oscillation Formula Underdamped solutions oscillate rapidly with the frequency and decay envelope described above. When the damping constant is small, b < \(\sqrt{4mk}\), the system oscillates while the amplitude of the motion decays exponentially. 1.1 drag and general damping forces. How do we model oscillatory phenomena in which air drag causes a decrease in oscillation amplitude? When a damped oscillator is underdamped,. Underdamped Oscillation Formula.
From pressbooks.library.torontomu.ca
7.1 Second Order Underdamped Systems Introduction to Control Systems Underdamped Oscillation Formula How do we model oscillatory phenomena in which air drag causes a decrease in oscillation amplitude? 1.1 drag and general damping forces. Frequency and graph the solution with initial conditions x(0). When the damping constant is small, b < \(\sqrt{4mk}\), the system oscillates while the amplitude of the motion decays exponentially. Underdamped solutions oscillate rapidly with the frequency and decay. Underdamped Oscillation Formula.
From www.youtube.com
Undamped, Underdamped, Critically Damped, and Overdamped Harmonic Underdamped Oscillation Formula When a damped oscillator is underdamped, it approaches zero faster than in the case of critical damping, but oscillates about that zero. How do we model oscillatory phenomena in which air drag causes a decrease in oscillation amplitude? When the damping constant is small, b < \(\sqrt{4mk}\), the system oscillates while the amplitude of the motion decays exponentially. (2) since. Underdamped Oscillation Formula.
From www.chegg.com
Solved 7) The Q of a damped oscillator Consider an Underdamped Oscillation Formula (2) since we have d=beta^2. Frequency and graph the solution with initial conditions x(0). How do we model oscillatory phenomena in which air drag causes a decrease in oscillation amplitude? Underdamped solutions oscillate rapidly with the frequency and decay envelope described above. 1.1 drag and general damping forces. When the damping constant is small, b < \(\sqrt{4mk}\), the system oscillates. Underdamped Oscillation Formula.